Zone - Area
| Zone | |
|---|---|
Symboles communs |
UNE |
| Unité SI | Mètre carré [m 2 ] |
| En unités de base SI | 1 m 2 |
| Dimension | |
L'aire est la quantité qui exprime l'étendue d'une région bidimensionnelle , d'une forme ou d'une lame plane , dans le plan . La surface est son analogue sur la surface bidimensionnelle d'un objet tridimensionnel . L'aire peut être comprise comme la quantité de matière d'une épaisseur donnée qui serait nécessaire pour façonner un modèle de la forme, ou la quantité de peinture nécessaire pour recouvrir la surface d'une seule couche. C'est l'analogue bidimensionnel de la longueur d'une courbe (un concept unidimensionnel) ou du volume d'un solide (un concept tridimensionnel).
L'aire d'une forme peut être mesurée en comparant la forme à des carrés de taille fixe. Dans le Système international d'unités (SI), l'unité standard de surface est le mètre carré (écrit m 2 ), qui est la surface d'un carré dont les côtés mesurent un mètre de long. Une forme d'une superficie de trois mètres carrés aurait la même superficie que trois de ces carrés. En mathématiques , le carré unitaire est défini comme ayant une aire un, et l'aire de toute autre forme ou surface est un nombre réel sans dimension .

Il existe plusieurs formules bien connues pour les zones de formes simples telles que les triangles , les rectangles et les cercles . En utilisant ces formules, l'aire de n'importe quel polygone peut être trouvée en divisant le polygone en triangles . Pour les formes avec une limite incurvée, le calcul est généralement nécessaire pour calculer la zone. En effet, le problème de la détermination de l'aire des figures planes a été une motivation majeure pour le développement historique du calcul .
Pour une forme solide telle qu'une sphère , un cône ou un cylindre, l'aire de sa surface limite est appelée aire de surface . Les formules pour les surfaces de formes simples ont été calculées par les anciens Grecs , mais le calcul de la surface d'une forme plus compliquée nécessite généralement un calcul multivariable .
L'aire joue un rôle important dans les mathématiques modernes. En plus de son importance évidente en géométrie et en calcul, l'aire est liée à la définition des déterminants en algèbre linéaire , et est une propriété de base des surfaces en géométrie différentielle . En analyse , l'aire d'un sous-ensemble du plan est définie à l'aide de la mesure de Lebesgue , bien que tous les sous-ensembles ne soient pas mesurables. En général, l'aire en mathématiques supérieures est considérée comme un cas particulier de volume pour les régions à deux dimensions.
La zone peut être définie à l'aide d'axiomes, la définissant en fonction d'une collection de certaines figures planes à l'ensemble des nombres réels. On peut prouver qu'une telle fonction existe.
Définition formelle
Une approche pour définir ce que l'on entend par « aire » se fait au moyen d' axiomes . « Aire » peut être définie comme une fonction d'une collection M d'un type particulier de figures planes (appelées ensembles mesurables) à l'ensemble de nombres réels, qui satisfait les propriétés suivantes :
- Pour tout S dans M , a ( S ) 0.
- Si S et T sont en M alors sont donc S ∪ T et S ∩ T , et aussi un ( S ∪ T ) = a ( S ) + un ( T ) - un ( S ∩ T ).
- Si S et T sont en M avec S ⊆ T puis T - S est en M et un ( T - S ) = a ( T ) - un ( S ).
- Si un ensemble S est dans M et S est congru à T alors T est aussi dans M et a ( S ) = a ( T ).
- Tout rectangle R est dans M . Si le rectangle a une longueur h et une largeur k alors a ( R ) = hk .
- Soit Q un ensemble compris entre deux régions de pas S et T . Une région de gradin est formée à partir d' une union finie de rectangles adjacents reposant sur une base commune, à savoir S ⊆ Q ⊆ T . S'il existe un nombre unique c tel que a ( S ) c a ( T ) pour toutes ces régions d' échelons S et T , alors a ( Q ) = c .
On peut prouver qu'une telle fonction de surface existe réellement.
Unités
Chaque unité de longueur a une unité d'aire correspondante, à savoir l'aire d'un carré avec la longueur de côté donnée. Ainsi, les surfaces peuvent être mesurées en mètres carrés (m 2 ), centimètres carrés (cm 2 ), millimètres carrés (mm 2 ), kilomètres carrés (km 2 ), pieds carrés (ft 2 ), yards carrés (yd 2 ), miles carrés (mi 2 ), et ainsi de suite. Algébriquement, ces unités peuvent être considérées comme les carrés des unités de longueur correspondantes.
L'unité SI de superficie est le mètre carré, qui est considéré comme une unité dérivée du SI .
Conversions
Le calcul de l'aire d'un carré dont la longueur et la largeur sont de 1 mètre serait :
1 mètre × 1 mètre = 1 m 2
et ainsi, un rectangle avec des côtés différents (disons une longueur de 3 mètres et une largeur de 2 mètres) aurait une aire en unités carrées qui peut être calculée comme :
3 mètres × 2 mètres = 6 m 2 . Cela équivaut à 6 millions de millimètres carrés. D'autres conversions utiles sont :
- 1 kilomètre carré = 1 000 000 mètres carrés
- 1 mètre carré = 10 000 centimètres carrés = 1 000 000 millimètres carrés
- 1 centimètre carré = 100 millimètres carrés.
Unités non métriques
En unités non métriques, la conversion entre deux unités carrées est le carré de la conversion entre les unités de longueur correspondantes.
la relation entre les pieds carrés et les pouces carrés est
- 1 pied carré = 144 pouces carrés,
où 144 = 12 2 = 12 × 12. De même :
- 1 mètre carré = 9 pieds carrés
- 1 mile carré = 3 097 600 verges carrés = 27 878 400 pieds carrés
De plus, les facteurs de conversion comprennent :
- 1 pouce carré = 6,4516 centimètres carrés
- 1 pied carré = 0,092 903 04 mètres carrés
- 1 mètre carré = 0,836 127 36 mètres carrés
- 1 mile carré = 2,589 988 110 336 kilomètres carrés
Autres unités dont historiques
Il existe plusieurs autres unités communes pour la zone. L' are était l'unité de surface d'origine dans le système métrique , avec :
- 1 are = 100 mètres carrés
Bien que l'are soit tombé en désuétude, l' hectare est encore couramment utilisé pour mesurer la terre :
- 1 hectare = 100 ares = 10 000 mètres carrés = 0,01 kilomètre carré
D'autres unités métriques de superficie peu communes incluent la tétrade , l' hectade et la myriade .
L' acre est aussi couramment utilisé pour mesurer la superficie des terres, où
- 1 acre = 4 840 verges carrés = 43 560 pieds carrés.
Un acre équivaut à environ 40 % d'un hectare.
À l'échelle atomique, la superficie est mesurée en unités de granges , telles que :
- 1 grange = 10 −28 mètres carrés.
La grange est couramment utilisée pour décrire la zone transversale d'interaction en physique nucléaire .
En Inde ,
- 20 dhurki = 1 dhur
- 20 dhur = 1 khatha
- 20 khata = 1 bigha
- 32 khata = 1 acre
Histoire
Zone du cercle
Au 5ème siècle avant notre ère, Hippocrate de Chios a été le premier à montrer que l'aire d'un disque (la région entourée d'un cercle) est proportionnelle au carré de son diamètre, dans le cadre de sa quadrature de la lune d'Hippocrate , mais n'a pas identifier la constante de proportionnalité . Eudoxe de Cnide , également au 5ème siècle avant notre ère, a également constaté que l'aire d'un disque est proportionnelle à son rayon au carré.
Par la suite, le Livre I d'Euclide Éléments eu affaire à l' égalité des zones entre les figures en deux dimensions. Le mathématicien Archimède a utilisé les outils de la géométrie euclidienne pour montrer que l'aire à l'intérieur d'un cercle est égale à celle d'un triangle rectangle dont la base a la longueur de la circonférence du cercle et dont la hauteur est égale au rayon du cercle, dans son livre Mesure d'un cercle . (La circonférence est égal à 2 π r , et l'aire d'un triangle est la moitié du temps de base de la hauteur, ce qui donne de la zone de r 2 pour le disque.) Archimède approchée de la valeur de π (et donc l'aire d'un cercle de rayon unité ) avec sa méthode de doublement , dans laquelle il a inscrit un triangle régulier dans un cercle et a noté son aire, puis a doublé le nombre de côtés pour donner un hexagone régulier , puis a doublé à plusieurs reprises le nombre de côtés à mesure que l'aire du polygone se rapprochait de plus en plus du cercle (et fait de même avec les polygones circonscrits ).
Scientifique suisse Johann Heinrich Lambert en 1761 a montré que π , le rapport de la superficie d'un cercle à son rayon au carré, est irrationnel , ce qui signifie qu'il ne soit pas égal au quotient de deux nombres entiers. En 1794, le mathématicien français Adrien-Marie Legendre a prouvé que π 2 est irrationnel ; cela prouve aussi que est irrationnel. En 1882, le mathématicien allemand Ferdinand von Lindemann a prouvé que π est transcendant (pas la solution d'une équation polynomiale avec des coefficients rationnels), confirmant une conjecture faite à la fois par Legendre et Euler.
Zone triangulaire
Héron (ou Héros) d'Alexandrie a trouvé ce que l'on appelle la formule de Héron pour l'aire d'un triangle en termes de ses côtés, et une preuve peut être trouvée dans son livre, Metrica , écrit vers 60 EC. Il a été suggéré qu'Archimède connaissait la formule plus de deux siècles plus tôt, et puisque Metrica est une collection des connaissances mathématiques disponibles dans le monde antique, il est possible que la formule soit antérieure à la référence donnée dans cet ouvrage.
En 499 Aryabhata , un grand mathématicien - astronome de l'âge classique des mathématiques indiennes et de l'astronomie indienne , a exprimé l'aire d'un triangle comme la moitié de la base multipliée par la hauteur dans l' Aryabhatiya (section 2.6).
Une formule équivalente à celle de Heron a été découverte par les Chinois indépendamment des Grecs. Il a été publié en 1247 dans Shushu Jiuzhang (" Traité mathématique en neuf sections "), écrit par Qin Jiushao .
Zone quadrilatérale
Au 7ème siècle de notre ère, Brahmagupta a développé une formule, maintenant connue sous le nom de formule de Brahmagupta , pour l'aire d'un quadrilatère cyclique (un quadrilatère inscrit dans un cercle) en termes de ses côtés. En 1842, les mathématiciens allemands Carl Anton Bretschneider et Karl Georg Christian von Staudt ont indépendamment trouvé une formule, connue sous le nom de formule de Bretschneider , pour l'aire de tout quadrilatère.
Superficie générale du polygone
Le développement des coordonnées cartésiennes par René Descartes au 17ème siècle a permis le développement de la formule de l' arpenteur pour l'aire de tout polygone avec des emplacements de sommet connus par Gauss au 19ème siècle.
Aires déterminées par calcul
Le développement du calcul intégral à la fin du XVIIe siècle a fourni des outils qui pourraient ensuite être utilisés pour calculer des zones plus complexes, telles que l'aire d'une ellipse et les aires de surface de divers objets tridimensionnels incurvés.
Formules de zone
Formules polygonales
Pour un polygone ( simple ) non auto-intersection , les coordonnées cartésiennes ( i =0, 1, ..., n -1) dont les n sommets sont connus, l'aire est donnée par la formule du géomètre :
où lorsque i = n -1, alors i +1 est exprimé en module n et fait donc référence à 0.
Rectangles
La formule d'aire la plus basique est la formule de l'aire d'un rectangle . Étant donné un rectangle de longueur l et de largeur w , la formule pour l'aire est :
- A = lw (rectangle).
C'est-à-dire que l'aire du rectangle est la longueur multipliée par la largeur. Comme cas particulier, comme l = w dans le cas d'un carré, l'aire d'un carré de côté s est donnée par la formule :
- A = s 2 (carré).
La formule de l'aire d'un rectangle découle directement des propriétés de base de l'aire et est parfois considérée comme une définition ou un axiome . D'autre part, si la géométrie est développée avant l' arithmétique , cette formule peut être utilisée pour définir la multiplication de nombres réels .
Dissection, parallélogrammes et triangles
La plupart des autres formules simples pour l'aire découlent de la méthode de dissection . Cela implique de découper une forme en morceaux, dont les aires doivent être égales à l'aire de la forme d'origine.
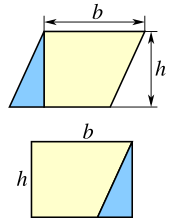
Par exemple, tout parallélogramme peut être subdivisé en un trapèze et un triangle rectangle , comme le montre la figure de gauche. Si le triangle est déplacé de l'autre côté du trapèze, la figure résultante est un rectangle. Il s'ensuit que l'aire du parallélogramme est la même que l'aire du rectangle :
- A = bh (parallélogramme).
Cependant, le même parallélogramme peut également être coupé le long d'une diagonale en deux triangles congrus , comme le montre la figure de droite. Il s'ensuit que l'aire de chaque triangle est la moitié de l'aire du parallélogramme :
- (Triangle).
Des arguments similaires peuvent être utilisés pour trouver des formules d'aire pour le trapèze ainsi que des polygones plus compliqués .
Zone de formes courbes
Cercles

La formule pour l'aire d'un cercle (plus correctement appelée l'aire délimitée par un cercle ou l'aire d'un disque ) est basée sur une méthode similaire. Étant donné un cercle de rayon r , il est possible de diviser le cercle en secteurs , comme le montre la figure de droite. Chaque secteur est de forme approximativement triangulaire et les secteurs peuvent être réarrangés pour former un parallélogramme approximatif. La hauteur de ce parallélogramme est r , et la largeur est la moitié de la circonférence du cercle, ou π r . Ainsi, l'aire totale du cercle est π r 2 :
- A = r 2 (cercle).
Bien que la dissection utilisée dans cette formule ne soit qu'approximative, l'erreur devient de plus en plus petite à mesure que le cercle est divisé en de plus en plus de secteurs. La limite des aires des parallélogrammes approchés est exactement π r 2 , qui est l'aire du cercle.
Cet argument est en fait une simple application des idées de calcul . Dans les temps anciens, la méthode de l'épuisement était utilisée de la même manière pour trouver l'aire du cercle, et cette méthode est maintenant reconnue comme un précurseur du calcul intégral . En utilisant des méthodes modernes, l'aire d'un cercle peut être calculée en utilisant une intégrale définie :
Ellipses
La formule de l'aire délimitée par une ellipse est liée à la formule d'un cercle ; pour une ellipse avec demi-grand et demi-petit axes x et y la formule est :
Superficie

La plupart des formules de base pour la surface peuvent être obtenues en coupant des surfaces et en les aplatissant. Par exemple, si la surface latérale d'un cylindre (ou de tout prisme ) est coupée dans le sens de la longueur, la surface peut être aplatie en un rectangle. De même, si une coupe est effectuée le long du côté d'un cône , la surface latérale peut être aplatie en un secteur de cercle et la zone résultante calculée.
La formule de l'aire de surface d'une sphère est plus difficile à dériver : parce qu'une sphère a une courbure de Gauss non nulle , elle ne peut pas être aplatie. La formule de la surface d'une sphère a été obtenue pour la première fois par Archimède dans son ouvrage Sur la sphère et le cylindre . La formule est :
- A = 4 πr 2 (sphère),
où r est le rayon de la sphère. Comme pour la formule de l'aire d'un cercle, toute dérivation de cette formule utilise intrinsèquement des méthodes similaires au calcul .
Formules générales
Zones de figures en 2 dimensions
- Un triangle : (où B est n'importe quel côté, et h est la distance de la ligne sur laquelle B se trouve à l'autre sommet du triangle). Cette formule peut être utilisée si la hauteur h est connue. Si les longueurs des trois côtés sont connues, alors la formule de Heron peut être utilisée : où a , b , c sont les côtés du triangle et représentent la moitié de son périmètre. Si un angle et ses deux côtés inclus sont donnés, la zone est où C est l'angle donné et a et b sont ses côtés inclus. Si le triangle est représenté graphiquement sur un plan de coordonnées, une matrice peut être utilisée et est simplifiée à la valeur absolue de . Cette formule est également connue sous le nom de formule de lacet et est un moyen facile de résoudre l'aire d'un triangle de coordonnées en substituant les 3 points (x 1 ,y 1 ) , (x 2 ,y 2 ) , et (x 3 ,y 3 ) . La formule du lacet peut également être utilisée pour trouver les aires d'autres polygones lorsque leurs sommets sont connus. Une autre approche pour un triangle de coordonnées consiste à utiliser le calcul pour trouver l'aire.
- Un polygone simple construit sur une grille de points équidistants (c'est-à-dire des points avec des coordonnées entières ) de telle sorte que tous les sommets du polygone soient des points de grille : , où i est le nombre de points de grille à l'intérieur du polygone et b est le nombre de points limites . Ce résultat est connu sous le nom de théorème de Pick .
Aire en calcul
- L'aire entre une courbe de valeur positive et l'axe horizontal, mesurée entre deux valeurs a et b (b est défini comme la plus grande des deux valeurs) sur l'axe horizontal, est donnée par l'intégrale de a à b de la fonction qui représente la courbe :
- L'aire entre les graphiques de deux fonctions est égale à l' intégrale d'une fonction , f ( x ), moins l'intégrale de l'autre fonction, g ( x ):
- où est la courbe avec la plus grande valeur y.
- Une aire délimitée par une fonction exprimée en coordonnées polaires est :
- L'aire délimitée par une courbe paramétrique à extrémités est donnée par les intégrales droites :
- ou la composante z de
- (Pour plus de détails, voir le théorème de Green § Calcul d'aire .) C'est le principe du dispositif mécanique planimètre .
Aire délimitée entre deux fonctions quadratiques
Pour trouver l'aire délimitée entre deux fonctions quadratiques , nous soustrayons l'une de l'autre pour écrire la différence sous la forme
où f ( x ) est la borne supérieure quadratique et g ( x ) est la borne inférieure quadratique. Définir le discriminant de f ( x ) -g ( x ) comme
En simplifiant la formule intégrale entre les graphiques de deux fonctions (comme indiqué dans la section ci-dessus) et en utilisant la formule de Vieta , nous pouvons obtenir
Ce qui précède reste valable si l'une des fonctions de délimitation est linéaire au lieu de quadratique.
Superficie des figures en 3 dimensions
- Cône : , où r est le rayon de la base circulaire, et h est la hauteur. Cela peut également être réécrit comme ou où r est le rayon et l est la hauteur d'inclinaison du cône. est la surface de base tandis que est la surface latérale du cône.
- cube : , où s est la longueur d'une arête.
- cylindre : , où r est le rayon d'une base et h est la hauteur. Le 2 r peut également être réécrit comme d , où d est le diamètre.
- prisme : 2B + Ph, où B est l'aire d'une base, P est le périmètre d'une base et h est la hauteur du prisme.
- pyramide : , où B est l'aire de la base, P est le périmètre de la base et L est la longueur de l'inclinaison.
- prisme rectangulaire : , où est la longueur, w est la largeur et h est la hauteur.
Formule générale pour la surface
La formule générale pour la surface du graphique d'une fonction continûment dérivable où et est une région dans le plan xy avec la frontière lisse :
Une formule encore plus générale pour l'aire du graphique d'une surface paramétrique sous la forme vectorielle où est une fonction vectorielle continûment dérivable de est :
Liste des formules
| Forme | Formule | Variables |
|---|---|---|
| Rectangle |

|
|
| Triangle |

|
|
| Triangle |

|
|
|
Triangle ( formule du héron ) |

|
|
| Triangle isocèle |

|
|
| Triangle régulier |

|
|
| Losange / Cerf - volant |

|
|
| Parallélogramme |

|
|
| trapèze |

|
|
| Hexagone régulier |

|
|
| Octogone régulier |

|
|
|
Polygone régulier ( côtés) |
|
( Périmètre ) incircle rayon circonscrit rayon
|
| Cercle |
( diamètre ) |

|
| Secteur circulaire |

|
|
| Ellipse |

|
|
| Intégral |

|
|
| Superficie | ||
|
Sphère |

|
|
| Cuboïde |

|
|
|
cylindre (incl. bas et haut) |

|
|
|
Cône (y compris le bas) |

|
|
| Torus |

|
|
| Surface de révolution |
(rotation autour de l'axe des x) |

|
Les calculs ci-dessus montrent comment trouver les zones de nombreuses formes courantes .
Les aires de polygones irréguliers (et donc arbitraires) peuvent être calculées à l'aide de la " formule de l'arpenteur " (formule du lacet).
Relation de l'aire au périmètre
L' inégalité isopérimétrique indique que, pour une courbe fermée de longueur L (donc la région qu'elle renferme a un périmètre L ) et pour l'aire A de la région qu'elle renferme,
et l'égalité est vraie si et seulement si la courbe est un cercle . Ainsi, un cercle a la plus grande aire de toute figure fermée avec un périmètre donné.
A l'autre extrême, une figure avec un périmètre donné L pourrait avoir une aire arbitrairement petite, comme illustré par un losange qui est "basculé" arbitrairement loin de sorte que deux de ses angles sont arbitrairement proches de 0° et les deux autres sont arbitrairement proches à 180°.
Pour un cercle, le rapport de l'aire à la circonférence (le terme pour le périmètre d'un cercle) est égal à la moitié du rayon r . Cela peut être vu à partir de la formule de l'aire πr 2 et de la formule de la circonférence 2 πr .
L'aire d'un polygone régulier est la moitié de son périmètre multiplié par l' apothème (où l'apothème est la distance entre le centre et le point le plus proche de n'importe quel côté).
Fractales
Doubler la longueur des bords d'un polygone multiplie sa surface par quatre, ce qui est deux (le rapport de la nouvelle longueur de côté à l'ancienne) augmenté à la puissance deux (la dimension de l'espace dans lequel réside le polygone). Mais si les longueurs unidimensionnelles d'une fractale dessinée en deux dimensions sont toutes doublées, le contenu spatial des échelles fractales s'échelonne d'une puissance de deux qui n'est pas nécessairement un nombre entier. Cette puissance est appelée la dimension fractale de la fractale.
Bissectrices d'aire
Il existe une infinité de droites qui coupent l'aire d'un triangle. Trois d'entre eux sont les médianes du triangle (qui relient les milieux des côtés aux sommets opposés), et celles-ci sont concurrentes au centre de gravité du triangle ; en effet, ce sont les seules bissectrices d'aire qui passent par le centroïde. Toute ligne passant par un triangle qui divise à la fois l'aire du triangle et son périmètre en deux passe par le centre du triangle (le centre de son cercle inscrit ). Il y en a un, deux ou trois pour un triangle donné.
Toute ligne passant par le milieu d'un parallélogramme coupe la zone en son milieu.
Toutes les bissectrices d'un cercle ou d'une autre ellipse passent par le centre et toutes les cordes passant par le centre coupent la zone en deux. Dans le cas d'un cercle, ce sont les diamètres du cercle.
Optimisation
Compte tenu d'un contour de fil, la surface de moindre surface couvrant ("remplissage") c'est une surface minimale . Les exemples familiers incluent les bulles de savon .
La question de l' aire de remplissage du cercle riemannien reste ouverte.
Le cercle a la plus grande surface de tout objet bidimensionnel ayant le même périmètre.
Un polygone cyclique (un inscrit dans un cercle) a la plus grande surface de tout polygone avec un nombre donné de côtés de même longueur.
Une version de l' inégalité isopérimétrique pour les triangles stipule que le triangle de plus grande aire parmi tous ceux ayant un périmètre donné est équilatéral .
Le triangle de plus grande aire de tous ceux inscrits dans un cercle donné est équilatéral ; et le triangle de plus petite aire de tous ceux circonscrits à un cercle donné est équilatéral.
Le rapport de l'aire du cercle inscrit à l'aire d'un triangle équilatéral, , est plus grand que celui de tout triangle non équilatéral.
Le rapport de l'aire au carré du périmètre d'un triangle équilatéral est plus grand que celui de tout autre triangle.
Voir également
- Brahmagupta quadrilatère , un quadrilatère cyclique avec des côtés entiers, des diagonales entières et une aire entière.
- Carte équiréaliste
- Triangle héronien , un triangle avec des côtés entiers et une aire entière.
- Liste des inégalités triangulaires
- Un septième triangle d'aire , un triangle intérieur avec un septième de l'aire du triangle de référence.
- Le théorème de Routh , une généralisation du triangle d'aire d'un septième.
- Ordres de grandeur : une liste de zones par taille.
- Dérivation de la formule d'un pentagone
- Planimètre , un instrument pour mesurer de petites zones, par exemple sur des cartes.
- Aire d'un quadrilatère convexe
- Pentagone de Robbins , un pentagone cyclique dont les longueurs des côtés et l'aire sont tous des nombres rationnels.






















































































![{\displaystyle A=2\pi \int _{a}^{b}\!f(x){\sqrt {1+\left[f'(x)\right]^{2}}}\mathrm { d} x}](https://wikimedia.org/api/rest_v1/media/math/render/svg/07cf6da325a77c650339de80d9b00d984ca3751d)


