Groupe Prüfer - Prüfer group

Le Prüfer 2 -group avec présentation ⟨ g _n : g _{n 1} ² = g _n , g ₁ ² = e ⟩ , illustré sous la forme d' un sous - groupe du cercle unité dans le plan complexe

En mathématiques, plus précisément en théorie des groupes , le p -groupe de Prüfer ou le p -groupe quasicyclique ou p ^∞ -groupe, Z ( p ^∞ ), pour un nombre premier p est l'unique p -groupe dans lequel chaque élément a p différent p -ème racines.

Les groupes p de Prüfer sont des groupes abéliens dénombrables qui sont importants dans la classification des groupes abéliens infinis: ils forment (avec le groupe des nombres rationnels ) les plus petits blocs de construction de tous les groupes divisibles .

Les groupes portent le nom de Heinz Prüfer , un mathématicien allemand du début du XXe siècle.

Constructions de Z ( p ^∞ )

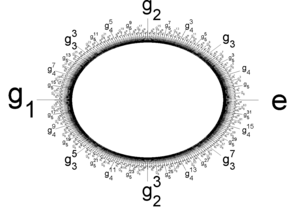
Le Prüfer p -group peut être identifié avec le sous - groupe du groupe de cercle , U (1), constitué de toutes les p ⁿ ième racines de l' unité en tant que n gammes plus de tous les nombres entiers non négatifs:

${\ displaystyle \ mathbf {Z} (p ^ {\ infty}) = \ {\ exp (2 \ pi im / p ^ {n}) \ mid 0 \ leq m <p ^ {n}, \, n \ in \ mathbf {Z} ^ {+} \} = \ {z \ in \ mathbf {C} \ mid z ^ {(p ^ {n})} = 1 {\ text {pour certains}} n \ in \ mathbf {Z} ^ {+} \}. \;}$

L'opération de groupe ici est la multiplication de nombres complexes .

Il y a une présentation

${\ displaystyle \ mathbf {Z} (p ^ {\ infty}) = \ langle \, g_ {1}, g_ {2}, g_ {3}, \ ldots \ mid g_ {1} ^ {p} = 1 , g_ {2} ^ {p} = g_ {1}, g_ {3} ^ {p} = g_ {2}, \ dots \, \ rangle.}$

Ici, l'opération de groupe en Z ( p ^∞ ) s'écrit comme multiplication.

En variante et de façon équivalente, la Prüfer p -group peut être définie comme la Sylow p -subgroup du groupe quotient Q / Z , consistant en les éléments dont l' ordre est une puissance de p :

${\ displaystyle \ mathbf {Z} (p ^ {\ infty}) = \ mathbf {Z} [1 / p] / \ mathbf {Z}}$

(où Z [1 / p ] désigne le groupe de tous les nombres rationnels dont le dénominateur est une puissance de p , en utilisant l'addition de nombres rationnels comme opération de groupe).

Pour chaque entier naturel n , considérons le groupe quotient Z / p ⁿ Z et l'inclusion Z / p ⁿ Z → Z / p ^{n +1} Z induite par la multiplication par p . La limite directe de ce système est Z ( p ^∞ ):

${\ displaystyle \ mathbf {Z} (p ^ {\ infty}) = \ varinjlim \ mathbf {Z} / p ^ {n} \ mathbf {Z}.}$

On peut aussi écrire

${\ displaystyle \ mathbf {Z} (p ^ {\ infty}) = \ mathbf {Q} _ {p} / \ mathbf {Z} _ {p}}$

où Q _p désigne le groupe additif des nombres p -adiques et Z _p est le sous-groupe des entiers p -adiques.

Propriétés

La liste complète des sous-groupes du p -groupe de Prüfer Z ( p ^∞ ) = Z [1 / p ] / Z est:

${\ displaystyle 0 \ subsetneq \ left ({1 \ over p} \ mathbf {Z} \ right) / \ mathbf {Z} \ subsetneq \ left ({1 \ over p ^ {2}} \ mathbf {Z} \ droite) / \ mathbf {Z} \ subsetneq \ left ({1 \ over p ^ {3}} \ mathbf {Z} \ right) / \ mathbf {Z} \ subsetneq \ cdots \ subsetneq \ mathbf {Z} (p ^ {\ infty})}$

(Voici un sous-groupe cyclique de Z ( p ^∞ ) avec p ⁿ éléments; il contient précisément les éléments de Z ( p ^∞ ) dont l' ordre divise p ⁿ et correspond à l'ensemble des p ⁿ -èmes racines de l'unité.) Le Prüfer Les p -groups sont les seuls groupes infinis dont les sous-groupes sont totalement ordonnés par inclusion. Cette séquence d'inclusions exprime le p- groupe de Prüfer comme la limite directe de ses sous-groupes finis. Comme il n'y a pas de sous-groupe maximal d'un p -groupe de Prüfer , il s'agit de son propre sous-groupe de Frattini . ${\ displaystyle \ left ({1 \ over p ^ {n}} \ mathbf {Z} \ right) / \ mathbf {Z}}$

Compte tenu de cette liste de sous-groupes, il est clair que les p -groupes de Prüfer sont indécomposables (ne peuvent pas être écrits comme une somme directe de sous-groupes propres). Plus est vrai: les groupes p de Prüfer sont sous- directement irréductibles . Un groupe abélien est sous-directement irréductible si et seulement s'il est isomorphe à un groupe p cyclique fini ou à un groupe de Prüfer.

Le groupe p de Prüfer est l'unique groupe p infini qui est localement cyclique (chaque ensemble fini d'éléments génère un groupe cyclique). Comme vu ci-dessus, tous les sous-groupes propres de Z ( p ^∞ ) sont finis. Les groupes p de Prüfer sont les seuls groupes abéliens infinis avec cette propriété.

Les groupes p de Prüfer sont divisibles . Ils jouent un rôle important dans la classification des groupes divisibles; avec les nombres rationnels, ce sont les groupes divisibles les plus simples. Plus précisément: un groupe abélien est divisible si et seulement s'il est la somme directe d'un nombre (éventuellement infini) de copies de Q et d'un nombre (éventuellement infini) de copies de Z ( p ^∞ ) pour tout p premier . Les nombres ( cardinaux ) de copies de Q et Z ( p ^∞ ) qui sont utilisés dans cette somme directe déterminent le groupe divisible jusqu'à l'isomorphisme.

En tant que groupe abélien (c'est-à-dire en tant que module Z ), Z ( p ^∞ ) est artinien mais pas noéthérien . Il peut donc être utilisé comme un contre-exemple contre l'idée que chaque module artinien est noéthérien (alors que chaque anneau artinien est noéthérien).

L' anneau d'endomorphisme de Z ( p ^∞ ) est isomorphe à l'anneau d' entiers p -adiques Z _p .

Dans la théorie des groupes topologiques localement compacts, le groupe p de Prüfer (doté de la topologie discrète ) est le dual de Pontryagin du groupe compact des entiers p -adiques , et le groupe des entiers p -adiques est le dual de Pontryagin du p de Prüfer p -groupe.

Voir également

• entiers p -adiques , qui peuvent être définis comme la limite inverse des sous-groupes finis du p -groupe dePrüfer.
• Nombres rationnels , rationnels dyadiques de la forme a / 2 ^b . Le groupe de Prüfer 2 peut être considéré comme les rationnels dyadiques modulo 1.
• Groupe cyclique ( analogue fini )
• Groupe de cercle ( analogique infiniment infini )

Remarques

Références

• Jacobson, Nathan (2009). Algèbre de base . 2 (2e éd.). Douvres. ISBN 978-0-486-47187-7.
• Pierre Antoine Grillet (2007). Algèbre abstraite . Springer. ISBN 978-0-387-71567-4.
• Kaplansky, Irving (1965). Groupes abéliens infinis . Presse de l'Université du Michigan.
• NN Vil'yams (2001) [1994], "Groupe quasi-cyclique" , Encyclopédie de mathématiques , EMS Press