Rationnel dyadique - Dyadic rational

Rationnels dyadiques dans l'intervalle de 0 à 1

En mathématiques, un rationnel dyadique ou rationnel binaire est un nombre qui peut s'exprimer comme une fraction dont le dénominateur est une puissance de deux . Par exemple, 1/2, 3/2 et 3/8 sont des rationnels dyadiques, mais 1/3 ne l'est pas. Ces nombres sont importants en informatique car ils sont les seuls à avoir des représentations binaires finies . Les rationnels dyadiques ont également des applications dans les poids et mesures, les signatures rythmiques musicales et l'enseignement précoce des mathématiques. Ils peuvent se rapprocher avec précision de n'importe quel nombre réel .

La somme, la différence ou le produit de deux nombres rationnels dyadiques est un autre nombre rationnel dyadique, donné par une formule simple. Cependant, la division d'un nombre rationnel dyadique par un autre ne produit pas toujours un résultat rationnel dyadique. Mathématiquement, cela signifie que les nombres rationnels dyadiques forment un anneau , situé entre l'anneau des nombres entiers et le corps des nombres rationnels . Cet anneau peut être noté . ${\displaystyle \mathbb {Z} [{\tfrac {1}{2}}]}$

En mathématiques avancées, les nombres rationnels dyadiques sont au cœur des constructions du solénoïde dyadique , la fonction point d'interrogation de Minkowski , ondelettes de Daubechies , le groupe de Thompson , Prüfer 2-groupe , nombres surréels et numéros thermocollants . Ces nombres sont d' ordre isomorphe aux nombres rationnels ; ils forment un sous-système des nombres 2-adiques ainsi que des réels, et peuvent représenter les parties fractionnaires des nombres 2-adiques. Des fonctions allant des nombres naturels aux rationnels dyadiques ont été utilisées pour formaliser l'analyse mathématique en mathématiques inversées .

Applications

En mesure

Poids de cuisine mesurant les fractions dyadiques d'une livre de 2 lb à 1/64 lb (1/4 oz)

De nombreux systèmes traditionnels de poids et de mesures sont basés sur l'idée de la réduction de moitié répétée, qui produit des rationnels dyadiques lors de la mesure de quantités fractionnaires d'unités. Le pouce est habituellement subdivisé en rationnels dyadiques plutôt que d'utiliser une subdivision décimale. Les divisions habituelles du gallon en demi-gallons, pintes , pintes et tasses sont également dyadiques. Les anciens Égyptiens utilisaient des rationnels dyadiques dans la mesure, avec des dénominateurs jusqu'à 64. De même, les systèmes de poids de la civilisation de la vallée de l' Indus sont pour la plupart basés sur des réductions de moitié répétées ; l'anthropologue Heather M.-L. Miller écrit que "la réduction de moitié est une opération relativement simple avec des balances à poutre, ce qui explique probablement pourquoi tant de systèmes de poids de cette période utilisaient des systèmes binaires".

En informatique

Les rationnels dyadiques sont au cœur de l' informatique en tant que type de nombre fractionnaire que de nombreux ordinateurs peuvent manipuler directement. En particulier, en tant que type de données utilisé par les ordinateurs, les nombres à virgule flottante sont souvent définis comme des nombres entiers multipliés par des puissances de deux positives ou négatives. Les nombres qui peuvent être représentés précisément dans un format à virgule flottante, tels que les types de données à virgule flottante IEEE , sont appelés ses nombres représentables. Pour la plupart des représentations à virgule flottante, les nombres représentables sont un sous-ensemble des rationnels dyadiques. La même chose est vraie pour les types de données à virgule fixe , qui utilisent également des puissances de deux implicitement dans la majorité des cas. En raison de la simplicité du calcul avec des rationnels dyadiques, ils sont également utilisés pour le calcul réel exact en utilisant l' arithmétique des intervalles et sont au cœur de certains modèles théoriques de nombres calculables .

La génération d'une variable aléatoire à partir de bits aléatoires, dans un laps de temps fixe, n'est possible que lorsque la variable a un nombre fini de résultats dont les probabilités sont toutes des nombres rationnels dyadiques. Pour les variables aléatoires dont les probabilités ne sont pas dyadiques, il faut soit approximer leurs probabilités par des rationnels dyadiques, soit utiliser un processus de génération aléatoire dont le temps est lui-même aléatoire et non borné.

En musique

Cinq barres de Igor Stravinski est Le Sacre du printemps
des signatures de temps³
₁₆, ²
₁₆, ³
₁₆, et ²
₈

Les signatures temporelles de la notation musicale occidentale sont traditionnellement écrites sous une forme ressemblant à des fractions (par exemple :²
₂, ⁴
₄, ou ⁶
₈), bien que la ligne horizontale de la portée musicale qui sépare le nombre supérieur et inférieur soit généralement omise lors de l'écriture de la signature séparément de sa portée. En tant que fractions, elles sont généralement dyadiques, bien que des signatures temporelles non dyadiques aient également été utilisées. La valeur numérique de la signature, interprétée comme une fraction, décrit la longueur d'une mesure comme une fraction d'une note entière . Son numérateur décrit le nombre de battements par mesure et le dénominateur décrit la longueur de chaque battement.

Dans l'enseignement des mathématiques

Dans les théories du développement chez l'enfant du concept de fraction basées sur les travaux de Jean Piaget , les nombres fractionnaires résultant de la réduction de moitié et de la réduction de moitié répétée sont parmi les premières formes de fractions à se développer. Cette étape de développement du concept de fractions a été appelée « division algorithmique ». L'addition et la soustraction de ces nombres peuvent être effectuées par étapes qui impliquent uniquement le doublement, la réduction de moitié, l'addition et la soustraction d'entiers. En revanche, l'addition et la soustraction de fractions plus générales impliquent une multiplication et une factorisation d'entiers pour atteindre un dénominateur commun. Par conséquent, les fractions dyadiques peuvent être plus faciles à calculer pour les élèves que les fractions plus générales.

Définitions et arithmétique

Les nombres dyadiques sont les nombres rationnels qui résultent de la division d'un nombre entier par une puissance de deux . Un nombre rationnel en termes simples est un rationnel dyadique quand est une puissance de deux. Une autre façon équivalente de définir les rationnels dyadiques est qu'ils sont les nombres réels qui ont une représentation binaire terminale . ${\displaystyle p/q}$${\style d'affichage q}$

L'addition , la soustraction et la multiplication de deux rationnels dyadiques quelconques produisent un autre rationnel dyadique, selon les formules suivantes :

${\displaystyle {\begin{aligned}{\frac {a}{2^{b}}}+{\frac {c}{2^{d}}}&={\frac {2}{d-\ min(b,d)}a+2^{b-\min(b,d)}c}{2^{\max(b,d)}}}\\[6px]{\frac {a}{ 2^{b}}}-{\frac {c}{2^{d}}}&={\frac {2^{d-\min(b,d)}a-2^{b-\min (b,d)}c}{2^{\max(b,d)}}}\\[6px]{\frac {a}{2^{b}}}\cdot {\frac {c}{ 2^{d}}}&={\frac {ac}{2^{b+d}}}\end{aligned}}}$

Cependant, le résultat de la division d' un rationnel dyadique par un autre n'est pas nécessairement un rationnel dyadique. Par exemple, 1 et 3 sont tous deux des nombres rationnels dyadiques, mais 1/3 ne l'est pas.

Propriétés supplémentaires

Approximations rationnelles dyadiques de la racine carrée de 2 ( ), trouvées en arrondissant au plus petit multiple entier le plus proche de pour La hauteur de la région rose au-dessus de chaque approximation est son erreur.${\displaystyle {\sqrt {2}}\environ 1.4142}$${\displaystyle 1/2^{i}}$${\displaystyle i=0,1,2,\dots }$

Nombres réels sans approximations rationnelles dyadiques inhabituellement précises. Les cercles rouges entourent les nombres dont l'erreur est approximée par . Pour les nombres dans le Cantor fractal situé en dehors des cercles, toutes les approximations rationnelles dyadiques ont des erreurs plus importantes.${\displaystyle {\tfrac {1}{6}}/2^{i}}$${\style d'affichage n/2^{i}}$

Tout entier, et tout demi-entier , est un rationnel dyadique. Ils répondent tous deux à la définition d'être un entier divisé par une puissance de deux : chaque entier est un entier divisé par un (la puissance zéro de deux), et chaque demi-entier est un entier divisé par deux.

Chaque nombre réel peut être arbitrairement étroitement approximé par des rationnels dyadiques. En particulier, pour un nombre réel , considérons les rationnels dyadiques de la forme , où peut être n'importe quel entier et désigne la fonction floor qui arrondit son argument à un entier inférieur. Ces nombres se rapprochent d'en bas à une erreur de , qui peut être rendue arbitrairement petite en choisissant d'être arbitrairement grande. Pour un sous-ensemble fractal des nombres réels, cette borne d'erreur est dans un facteur constant d'optimal : pour ces nombres, il n'y a pas d'approximation avec une erreur inférieure à une constante fois . L'existence d'approximations dyadiques précises peut être exprimée en disant que l'ensemble de tous les rationnels dyadiques est un dense dans la ligne réelle . Plus fortement, cet ensemble est uniformément dense, en ce sens que les rationnels dyadiques au dénominateur sont uniformément espacés sur la droite réelle. ${\style d'affichage x}$${\textstyle \lfloor 2^{i}x\rfloor /2^{i}}$${\style d'affichage i}$${\displaystyle \lfloor \dots \rfloor }$${\style d'affichage x}$${\displaystyle 1/2^{i}}$${\style d'affichage i}$${\style d'affichage n/2^{i}}$${\displaystyle 1/2^{i}}$${\style d'affichage 2^{i}}$

Les rationnels dyadiques sont précisément ces nombres possédant des développements binaires finis . Leurs développements binaires ne sont pas uniques ; il existe une représentation finie et une représentation infinie de chaque rationnel dyadique autre que 0 (en ignorant les 0 terminaux). Par exemple, 0,11 ₂ = 0,10111... ₂ , donnant deux représentations différentes pour 3/4. Les rationnels dyadiques sont les seuls nombres dont les développements binaires ne sont pas uniques.

En mathématiques avancées

Structure algébrique

Parce qu'ils sont fermés par addition, soustraction et multiplication, mais pas par division, les rationnels dyadiques sont un anneau mais pas un corps . L'anneau des rationnels dyadiques peut être noté , ce qui signifie qu'il peut être généré en évaluant des polynômes à coefficients entiers, à l'argument 1/2. En tant qu'anneau, les rationnels dyadiques sont un sous - anneau des nombres rationnels et un dépassement des nombres entiers. Algébriquement, cet anneau est la localisation des entiers par rapport à l'ensemble des puissances de deux . ${\displaystyle \mathbb {Z} [{\tfrac {1}{2}}]}$

En plus de former un sous-anneau des nombres réels , les nombres rationnels dyadiques forment un sous-anneau des nombres 2-adiques , un système de nombres qui peut être défini à partir de représentations binaires finies à droite du point binaire mais pouvant s'étendre à l'infini. loin à gauche. Les nombres 2-adiques incluent tous les nombres rationnels, pas seulement les rationnels dyadiques. L'intégration des rationnels dyadiques dans les nombres 2-adiques ne change pas l'arithmétique des rationnels dyadiques, mais cela leur donne une structure topologique différente de celle qu'ils ont en tant que sous-anneau des nombres réels. Comme ils le font dans les réels, les rationnels dyadiques forment un sous-ensemble dense des nombres 2-adiques, et sont l'ensemble des nombres 2-adiques avec des développements binaires finis. Chaque nombre 2-adique peut être décomposé en la somme d'un entier 2-adique et d'un rationnel dyadique ; en ce sens, les rationnels dyadiques peuvent représenter les parties fractionnaires des nombres 2-adiques, mais cette décomposition n'est pas unique.

L'addition des rationnels dyadiques modulo 1 (le groupe quotient des rationnels dyadiques par les entiers) forme le 2-groupe de Prüfer . ${\displaystyle \mathbb {Z} [{\tfrac {1}{2}}]/\mathbb {Z} }$

Solénoïde dyadique

Ne considérer que les opérations d'addition et de soustraction des rationnels dyadiques leur donne la structure d'un groupe abélien additif . La dualité de Pontryagin est une méthode pour comprendre les groupes abéliens en construisant des groupes duaux, dont les éléments sont des caractères du groupe d'origine, des homomorphismes de groupe au groupe multiplicatif des nombres complexes , avec la multiplication par points comme opération de groupe duel. Le groupe dual des rationnels dyadiques additifs, ainsi construit, peut également être considéré comme un groupe topologique . Il est appelé solénoïde dyadique et est isomorphe au produit topologique des nombres réels et des nombres 2-adiques, quotient par le plongement diagonal des rationnels dyadiques dans ce produit. C'est un exemple d'un protorus , d'un solénoïde et d'un continuum indécomposable .

Fonctions avec des rationnels dyadiques comme points distingués

La fonction de point d'interrogation de Minkowski fait correspondre les nombres rationnels aux rationnels dyadiques

Une ondelette de Daubechies , montrant des points de non-lissage au niveau des rationnels dyadiques

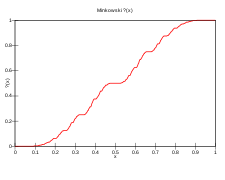
Parce qu'ils sont un sous-ensemble dense des nombres réels, les rationnels dyadiques, avec leur ordre numérique, forment un ordre dense . Comme avec deux ordres linéaires denses dénombrables non bornés, par le théorème d'isomorphisme de Cantor , les rationnels dyadiques sont ordre-isomorphes aux nombres rationnels. Dans ce cas, la fonction de point d'interrogation de Minkowski fournit une bijection préservant l'ordre entre l'ensemble de tous les nombres rationnels et l'ensemble des rationnels dyadiques.

Les rationnels dyadiques jouent un rôle clé dans l'analyse des ondelettes de Daubechies , en tant qu'ensemble de points où la fonction d'échelle de ces ondelettes n'est pas lisse. De même, les rationnels dyadiques paramétrent les discontinuités de la frontière entre les points stables et instables dans l'espace des paramètres de l'application de Hénon .

L'ensemble des homéomorphismes linéaires par morceaux de l' intervalle unitaire à lui-même qui ont des pentes de puissance de 2 et des points de rupture dyadiques-rationnels forment un groupe sous l'opération de composition de fonction . Il s'agit du groupe de Thompson , le premier exemple connu d'un groupe simple infini mais de présentation finie . Le même groupe peut aussi être représenté par une action sur les arbres binaires enracinés, ou par une action sur les rationnels dyadiques dans l'intervalle unitaire.

Autres constructions connexes

En mathématiques inversées , une façon de construire les nombres réels consiste à les représenter comme des fonctions allant des nombres unaires aux rationnels dyadiques, où la valeur de l'une de ces fonctions pour l'argument est un rationnel dyadique avec un dénominateur qui se rapproche du nombre réel donné. La définition des nombres réels de cette manière permet à de nombreux résultats de base de l'analyse mathématique d'être prouvés au sein d'une théorie restreinte de l' arithmétique du second ordre appelée « analyse faisable » (BTFA). ${\style d'affichage i}$${\style d'affichage 2^{i}}$

Les nombres surréalistes sont générés par un principe de construction itéré qui commence par générer tous les rationnels dyadiques finis, puis continue pour créer de nouveaux et étranges types de nombres infinis, infinitésimaux et autres. Ce système de nombres est à la base de la théorie des jeux combinatoires , et les rationnels dyadiques apparaissent naturellement dans cette théorie comme l'ensemble des valeurs de certains jeux combinatoires.

Les nombres fusibles sont un sous-ensemble des rationnels dyadiques, la fermeture de l'ensemble sous l'opération , restreinte aux paires avec . Ils sont bien ordonnés , avec un type de commande égal au nombre epsilon . Pour chaque entier, le plus petit nombre fusible supérieur à a la forme . L'existence de for each ne peut pas être prouvée en arithmétique de Peano , et croît si rapidement en fonction de cela car il est (dans la notation de Knuth avec flèche vers le haut pour les grands nombres) déjà plus grand que . ${\style d'affichage \{0\}}$${\displaystyle x,y\mapsto (x+y+1)/2}$${\style d'affichage x,y}$${\style d'affichage |xy|<1}$ ${\displaystyle \varepsilon _{0}}$${\style d'affichage n}$${\style d'affichage n}$${\style d'affichage n+1/2^{k}}$${\style d'affichage k}$${\style d'affichage n}$${\style d'affichage k}$${\style d'affichage n}$${\style d'affichage n=3}$${\displaystyle 2\uparrow ^{9}16}$

Les références