Modèle Debye - Debye model

Mécanique statistique
Thermodynamique Théorie cinétique
Statistiques de particules Théorème des statistiques de spin Particules identiques Maxwell–Boltzmann Bose-Einstein Fermi-Dirac Parastatistique Statistiques anyoniques Statistiques de tresse
Ensembles thermodynamiques NVE Microcanonique NVT Canonique µVT Grand canonique NPH Isoenthalpique–isobare NPT Isotherme–isobare
Des modèles Au revoir Einstein Je chante Potts
Potentiels Énergie interne Enthalpie L'énergie libre de Helmholtz L'énergie gratuite de Gibbs Grand potentiel / Landau énergie libre
Scientifiques Maxwell Boltzmann Gibbs Einstein Ehrenfest von Neumann Tolman Au revoir Fermi Bose
v t e

En thermodynamique et en physique du solide , le modèle de Debye est une méthode développée par Peter Debye en 1912 pour estimer la contribution des phonons à la chaleur spécifique (capacité calorifique) dans un solide . Il traite les vibrations du réseau atomique (chaleur) comme des phonons dans une boîte, contrairement au modèle d'Einstein , qui traite le solide comme de nombreux oscillateurs harmoniques quantiques individuels sans interaction . Le modèle de Debye prédit correctement la faible dépendance à la température de la capacité calorifique, qui est proportionnelle à – la loi de Debye T ³ . Tout comme le modèle d'Einstein , il récupère également la loi de Dulong-Petit à haute température. Mais en raison d'hypothèses simplificatrices, sa précision souffre à des températures intermédiaires. ${\displaystyle T^{3}}$

Dérivation

Le modèle de Debye est un équivalent à l'état solide de la loi de Planck sur le rayonnement du corps noir , où l'on traite le rayonnement électromagnétique comme un gaz photonique . Le modèle de Debye traite les vibrations atomiques comme des phonons dans une boîte (la boîte étant le solide). La plupart des étapes de calcul sont identiques car les deux sont des exemples d'un gaz de Bose sans masse avec une relation de dispersion linéaire .

Considérons un cube de côté . A partir de la particule dans un article de boîte , les modes de résonance des perturbations sonores à l'intérieur de la boîte (en ne considérant pour l'instant que ceux alignés sur un axe) ont des longueurs d'onde données par ${\style d'affichage L}$

${\displaystyle \lambda _{n}={2L \over n}\,,}$

où est un entier. L'énergie d'un phonon est ${\style d'affichage n}$

${\displaystyle E_{n}\ =h\nu _{n}\,,}$

où est la constante de Planck et est la fréquence du phonon. En faisant l'approximation que la fréquence est inversement proportionnelle à la longueur d'onde, nous avons ${\style d'affichage h}$${\style d'affichage \nu _{n}}$

${\displaystyle E_{n}=h\nu _{n}={hc_{\rm {s}} \over \lambda _{n}}={hc_{s}n \over 2L}\,,}$

dans laquelle est la vitesse du son à l'intérieur du solide. En trois dimensions nous utiliserons ${\displaystyle c_{s}}$

${\displaystyle E_{n}^{2}={p_{n}^{2}c_{\rm {s}}^{2}}=\left({hc_{\rm {s}} \over 2L }\right)^{2}\left(n_{x}^{2}+n_{y}^{2}+n_{z}^{2}\right)\,,}$

dans laquelle est l'amplitude de la quantité de mouvement tridimensionnelle du phonon. ${\style d'affichage p_{n}}$

L'approximation selon laquelle la fréquence est inversement proportionnelle à la longueur d'onde (donnant une vitesse constante du son) est bonne pour les phonons de basse énergie mais pas pour les phonons de haute énergie (voir l'article sur les phonons ). modèle de Debye, et produit des résultats incorrects à des températures intermédiaires, alors qu'aux limites de basse et haute température les résultats sont exacts.

Calculons maintenant l'énergie totale dans la boîte,

${\displaystyle E=\sum _{n}E_{n}\,{\bar {N}}(E_{n})\,,}$

où est le nombre de phonons dans la boîte avec de l'énergie . En d'autres termes, l'énergie totale est égale à la somme de l'énergie multipliée par le nombre de phonons avec cette énergie (dans une dimension). En 3 dimensions nous avons : ${\displaystyle {\bar {N}}(E_{n})}$${\style d'affichage E_{n}}$

${\displaystyle U=\sum _{n_{x}}\sum _{n_{y}}\sum _{n_{z}}E_{n}\,{\bar {N}}(E_{n} )\,.}$

Ici, le modèle de Debye et la loi de Planck du rayonnement du corps noir diffèrent. Contrairement au rayonnement électromagnétique dans une boîte, il existe un nombre fini d' états d'énergie des phonons car un phonon ne peut pas avoir des fréquences arbitrairement élevées. Sa fréquence est limitée par le milieu de sa propagation, le réseau atomique du solide. Considérons une illustration d'un phonon transverse ci-dessous.

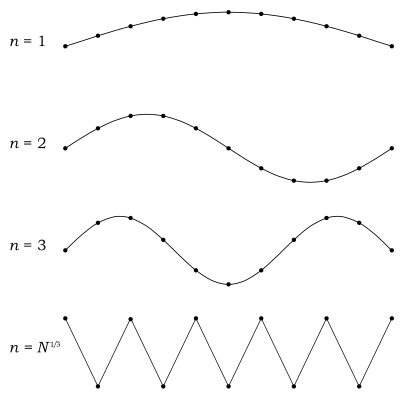
Il est raisonnable de supposer que la longueur d'onde minimale d'un phonon est le double de la séparation des atomes, comme le montre la figure du bas. Il y a des atomes dans un solide. Notre solide est un cube, ce qui signifie qu'il y a des atomes par arête. La séparation des atomes est alors donnée par , et la longueur d'onde minimale est ${\style d'affichage N}$${\displaystyle {\sqrt[{3}]{N}}}$${\displaystyle L/{\sqrt[{3}]{N}}}$

${\displaystyle \lambda _{\rm {min}}={2L \over {\sqrt[{3}]{N}}}\,,}$

faire le nombre de mode maximum (infini pour les photons ) ${\style d'affichage n}$

${\displaystyle n_{\rm {max}}={\sqrt[{3}]{N}}\,.}$

Ce nombre limite la limite supérieure de la somme d'énergie triple

${\displaystyle U=\sum _{n_{x}}^{\sqrt[{3}]{N}}\sum _{n_{y}}^{\sqrt[{3}]{N}}\ somme _{n_{z}}^{\sqrt[{3}]{N}}E_{n}\,{\bar {N}}(E_{n})\,.}$

Pour les fonctions qui varient lentement et qui se comportent bien, une somme peut être remplacée par une intégrale (également connue sous le nom d' approximation de Thomas-Fermi )

${\displaystyle U\approx \int _{0}^{\sqrt[{3}]{N}}\int _{0}^{\sqrt[{3}]{N}}\int _{0} ^{\sqrt[{3}]{N}}E(n)\,{\bar {N}}\left(E(n)\right)\,dn_{x}\,dn_{y}\, dn_{z}\,.}$

Jusqu'à présent, il n'y a eu aucune mention de , le nombre de phonons d'énergie Les phonons obéissent aux statistiques de Bose-Einstein . Leur distribution est donnée par la célèbre formule de Bose-Einstein ${\displaystyle {\bar {N}}(E)}$${\style d'affichage E\,.}$

${\displaystyle \langle N\rangle _{BE}={1 \over e^{E/kT}-1}\,.}$

Parce qu'un phonon a trois états de polarisation possibles (un longitudinal et deux transverses qui n'affectent pas approximativement son énergie), la formule ci-dessus doit être multipliée par 3,

${\displaystyle {\bar {N}}(E)={3 \over e^{E/kT}-1}\,.}$

(En fait on utilise une vitesse sonique effective , c'est-à-dire que la température de Debye (voir ci-dessous) est proportionnelle à , plus précisément , où l'on distingue les vitesses d'onde sonore longitudinale et transversale (contributions 1/3 et 2/3, respectivement). La température de Debye ou la vitesse sonique effective est une mesure de la dureté du cristal.) ${\displaystyle c_{s}:=c_{\rm {eff}}}$${\displaystyle T_{\rm {D}}}$${\displaystyle c_{\rm {eff}}}$${\displaystyle T_{\rm {D}}^{-3}\propto c_{\rm {eff}}^{-3} :=(1/3)c_{\rm {long}}^{-3 }+(2/3)c_{\rm {trans}}^{-3}}$

Substitution dans l'intégrale énergétique des rendements

${\displaystyle U=\int _{0}^{\sqrt[{3}]{N}}\int _{0}^{\sqrt[{3}]{N}}\int _{0}^ {\sqrt[{3}]{N}}E(n)\,{3 \over e^{E(n)/kT}-1}\,dn_{x}\,dn_{y}\,dn_ {z}\,.}$

La facilité avec laquelle ces intégrales sont évaluées pour les photons est due au fait que la fréquence de la lumière, au moins semi-classiquement, n'est pas liée. Comme l'illustre la figure ci-dessus, ce n'est pas vrai pour les phonons . Afin d'approcher cette triple intégrale, Debye a utilisé des coordonnées sphériques

${\displaystyle \ (n_{x},n_{y},n_{z})=(n\sin \theta \cos \phi ,n\sin \theta \sin \phi ,n\cos \theta )}$

et approximé le cube par un huitième de sphère

${\displaystyle U\approx \int _{0}^{\pi /2}\int _{0}^{\pi /2}\int _{0}^{R}E(n)\,{3 \over e^{E(n)/kT}-1}n^{2}\sin \theta \,dn\,d\theta \,d\phi \,,}$

où est le rayon de cette sphère, que l'on trouve en conservant le nombre de particules dans le cube et dans le huitième de sphère. Le volume du cube est un volume de maille , ${\style d'affichage R}$${\style d'affichage N}$

${\displaystyle N={1 \over 8}{4 \over 3}\pi R^{3}\,,}$

donc on obtient

${\displaystyle R={\sqrt[{3}]{6N \over \pi }}\,.}$

La substitution de l'intégration sur une sphère pour l'intégrale correcte introduit une autre source d'imprécision dans le modèle.

L'intégrale énergétique devient

${\displaystyle U={3\pi \over 2}\int _{0}^{R}\,{hc_{s}n \over 2L}{n^{2} \over e^{hc_{\rm {s}}n/2LkT}-1}\,dn}$

Changer la variable d'intégration en , ${\displaystyle x={hc_{\rm {s}}n \over 2LkT}}$

${\displaystyle U={3\pi \over 2}kT\left({2LkT \over hc_{\rm {s}}}\right)^{3}\int _{0}^{hc_{\rm { s}}R/2LkT}{x^{3} \over e^{x}-1}\,dx}$

Pour simplifier l'apparence de cette expression, définissez la température de Debye ${\displaystyle T_{\rm {D}}}$

${\displaystyle T_{\rm {D}}\ {\stackrel {\mathrm {def} }{=}}\ {hc_{\rm {s}}R \over 2Lk}={hc_{\rm {s} } \over 2Lk}{\sqrt[{3}]{6N \over \pi }}={hc_{\rm {s}} \over 2k}{\sqrt[{3}]{{6 \over \pi }{N \sur V}}}}$

où est le volume de la boîte cubique de côté . ${\style d'affichage V}$${\style d'affichage L}$

De nombreuses références décrivent la température de Debye comme un simple raccourci pour certaines constantes et variables dépendantes du matériau. Cependant, comme indiqué ci-dessous, est à peu près égale à l'énergie des phonons du mode de longueur d'onde minimale, et nous pouvons donc interpréter la température de Debye comme la température à laquelle le mode de fréquence la plus élevée (et donc chaque mode) est excité. ${\displaystyle kT_{\rm {D}}}$

En continuant, nous avons alors l'énergie interne spécifique :

${\displaystyle {\frac {U}{Nk}}=9T\left({T \over T_{\rm {D}}}\right)^{3}\int _{0}^{T_{\rm {D}}/T}{x^{3} \over e^{x}-1}\,dx=3TD_{3}\left({T_{\rm {D}} \over T}\right) \,,}$

où est la (troisième) fonction Debye . ${\style d'affichage D_{3}(x)}$

En différenciant par rapport à nous obtenons la capacité calorifique sans dimension : ${\style d'affichage T}$

${\displaystyle {\frac {C_{V}}{Nk}}=9\left({T \over T_{\rm {D}}}\right)^{3}\int _{0}^{T_ {\rm {D}}/T}{x^{4}e^{x} \over \left(e^{x}-1\right)^{2}}\,dx\,.}$

Ces formules traitent le modèle Debye à toutes les températures. Les formules plus élémentaires données plus bas donnent le comportement asymptotique dans la limite des basses et hautes températures. Comme déjà mentionné, ce comportement est exact, contrairement au comportement intermédiaire. La raison essentielle de l'exactitude aux basses et hautes énergies, respectivement, est que le modèle de Debye donne (i) la relation exacte de dispersion aux basses fréquences, et (ii) correspond à la densité exacte d'états , concernant le nombre de vibrations par fréquence intervalle. ${\style d'affichage E(\nu )}$ ${\displaystyle (\int g(\nu )\,{\rm {d\nu }}\equiv 3N)\,}$

Dérivation de Debye

Debye a dérivé son équation un peu différemment et plus simplement. En utilisant la mécanique des milieux continus , il a découvert que le nombre d' états vibrationnels avec une fréquence inférieure à une valeur particulière était asymptotique à

${\displaystyle n\sim {1 \over 3}\nu ^{3}VF\,,}$

dans lequel est le volume et est un facteur qu'il a calculé à partir des coefficients d'élasticité et de la densité. La combinaison de cette formule avec l'énergie attendue d'un oscillateur harmonique à la température T (déjà utilisé par Einstein dans son modèle) donnerait une énergie de ${\style d'affichage V}$${\style d'affichage F}$

${\displaystyle U=\int _{0}^{\infty }\,{h\nu ^{3}VF \over e^{h\nu /kT}-1}\,d\nu \,,}$

si les fréquences vibrationnelles continuaient à l'infini. Cette forme donne le comportement qui est correct à basse température. Mais Debye s'est rendu compte qu'il ne pouvait y avoir que des états vibrationnels pour N atomes. Il a fait l'hypothèse que dans un solide atomique, le spectre des fréquences des états vibrationnels continuerait à suivre la règle ci-dessus, jusqu'à une fréquence maximale choisie de telle sorte que le nombre total d'états soit : ${\displaystyle T^{3}}$${\style d'affichage 3N}$${\style d'affichage \nu _{m}}$${\style d'affichage 3N}$

${\displaystyle 3N={1 \over 3}\nu _{m}^{3}VF\,.}$

Debye savait que cette hypothèse n'était pas vraiment correcte (les fréquences les plus élevées sont plus rapprochées que supposé), mais elle garantit le bon comportement à haute température ( loi de Dulong-Petit ). L'énergie est alors donnée par

${\displaystyle U=\int _{0}^{\nu _{m}}\,{h\nu ^{3}VF \over e^{h\nu /kT}-1}\,d\nu \,,}$

${\displaystyle =VFkT(kT/h)^{3}\int _{0}^{T_{\rm {D}}/T}\,{x^{3} \over e^{x}-1 }\,dx\,,}$

où est .${\displaystyle T_{\rm {D}}}$${\displaystyle h\nu _{m}/k}$

${\displaystyle =9NkT(T/T_{\rm {D}})^{3}\int _{0}^{T_{\rm {D}}/T}\,{x^{3} \over e^{x}-1}\,dx\,,}$

${\displaystyle =3NkTD_{3}(T_{\rm {D}}/T)\,,}$

où est la fonction qui a reçu plus tard le nom de fonction Debye de troisième ordre . ${\style d'affichage D_{3}}$

Une autre dérivation

D'abord, nous dérivons la distribution de fréquence vibrationnelle; la dérivation suivante est basée sur l'annexe VI de. Considérons un solide élastique isotrope tridimensionnel avec N atomes sous la forme d'un parallélépipède rectangle de longueurs latérales . L'onde élastique obéira à l' équation des ondes et sera des ondes planes ; considérer le vecteur d'onde et définir . Notez que nous avons ${\style d'affichage L_{x},L_{y},L_{z}}$ ${\displaystyle \mathbf {k} =(k_{x},k_{y},k_{z})}$${\displaystyle l_{x}={\frac {k_{x}}{|\mathbf {k} |}},l_{y}={\frac {k_{y}}{|\mathbf {k} | }},l_{z}={\frac {k_{z}}{|\mathbf {k} |}}}$

${\displaystyle l_{x}^{2}+l_{y}^{2}+l_{z}^{2}=1.}$

( 1 )

Les solutions de l' équation des ondes sont

${\displaystyle u(x,y,z,t)=\sin(2\pi \nu t)\sin \left({\frac {2\pi l_{x}x}{\lambda }}\right) \sin \left({\frac {2\pi l_{y}y}{\lambda }}\right)\sin \left({\frac {2\pi l_{z}z}{\lambda }}\ droit)}$

et avec les conditions aux limites en , on a ${\style d'affichage u=0}$${\style d'affichage x,y,z=0,x=L_{x},y=L_{y},z=L_{z}}$

${\displaystyle {\frac {2l_{x}L_{x}}{\lambda }}=n_{x} ;{\frac {2l_{y}L_{y}}{\lambda }}=n_{y} ;{\frac {2l_{z}L_{z}}{\lambda }}=n_{z}}$

( 2 )

où sont des entiers positifs. En remplaçant ( 2 ) dans ( 1 ) et en utilisant également la relation de dispersion , nous avons ${\style d'affichage n_{x},n_{y},n_{z}}$ ${\displaystyle c_{s}=\lambda \nu }$

${\displaystyle {\frac {n_{x}^{2}}{(2\nu L_{x}/c_{s})^{2}}}+{\frac {n_{y}^{2} }{(2\nu L_{y}/c_{s})^{2}}}+{\frac {n_{z}^{2}}{(2\nu L_{z}/c_{s} )^{2}}}=1.}$

L'équation ci-dessus, pour une fréquence fixe , décrit un huitième d'ellipse dans "l'espace des modes" (un huitième car sont positifs). Le nombre de modes de fréquence inférieure à est donc le nombre de points entiers à l'intérieur de l'ellipse, qui, dans la limite de (c'est-à-dire pour un très grand parallélépipède) peut être approché du volume de l'ellipse. Par conséquent, le nombre de modes avec une fréquence dans la gamme est ${\style d'affichage \nu }$${\style d'affichage n_{x},n_{y},n_{z}}$${\style d'affichage \nu }$${\displaystyle L_{x},L_{y},L_{z}\to \infty }$${\style d'affichage N(\nu )}$${\style d'affichage [0,\nu ]}$

${\displaystyle N(\nu )={\frac {1}{8}}{\frac {4\pi }{3}}\left({\frac {2\nu }{c_{\mathrm {s} }}}\right)^{3}L_{x}L_{y}L_{z}={\frac {4\pi \nu ^{3}V}{3c_{\mathrm {s} }^{3 }}},}$

( 3 )

où est le volume du parallélépipède. A noter que la vitesse des ondes dans la direction longitudinale est différente de la direction transversale et que les ondes peuvent être polarisées dans un sens dans le sens longitudinal et dans les deux sens dans le sens transversal ; ainsi définissons-nous . ${\displaystyle V=L_{x}L_{y}L_{z}}$${\displaystyle {\frac {3}{c_{s}^{3}}}={\frac {1}{c_{\text{long}}^{3}}}+{\frac {2}{ c_{\text{trans}}^{3}}}}$

Suite à la dérivation de, nous définissons une limite supérieure à la fréquence de vibration ; puisqu'il y a N atomes dans le solide, il y a 3N oscillateurs harmoniques quantiques (3 pour chaque direction x, y, z) oscillant sur la gamme de fréquences . On peut donc déterminer ainsi : ${\style d'affichage \nu _{D}}$${\style d'affichage [0,\nu _{D}]}$${\style d'affichage \nu _{D}}$

${\displaystyle 3N=N(\nu _{\rm {D}})={\frac {4\pi \nu _{\rm {D}}^{3}V}{3c_{\rm {s} }^{3}}}}$.

( 4 )

En définissant , où k est la constante de Boltzmann et h est la constante de Planck , et en substituant ( 4 ) dans ( 3 ), nous obtenons ${\displaystyle \nu _{\rm {D}}={\frac {kT_{\rm {D}}}{h}}}$

${\displaystyle N(\nu )={\frac {3Nh^{3}\nu ^{3}}{k^{3}T_{\rm {D}}^{3}}},}$

( 5 )

cette définition est plus standard. Nous pouvons trouver la contribution énergétique de tous les oscillateurs oscillant à la fréquence . Les oscillateurs harmoniques quantiques peuvent avoir des énergies où et en utilisant les statistiques de Maxwell-Boltzmann , le nombre de particules avec de l'énergie est ${\style d'affichage \nu }$${\displaystyle E_{i}=(i+1/2)h\nu }$${\displaystyle i=0,1,2,\dotsc }$${\style d'affichage E_{i}}$

${\displaystyle n_{i}={\frac {1}{A}}e^{-E_{i}/(kT)}={\frac {1}{A}}e^{-(i+1 /2)h\nu /(kT)}}$.

La contribution d'énergie pour les oscillateurs avec fréquence est alors ${\style d'affichage \nu }$

${\displaystyle dU(\nu )=\sum _{i=0}^{\infty }E_{i}{\frac {1}{A}}e^{-E_{i}/(kT)}}$.

( 6 )

En notant que (car il y a des modes oscillant avec la fréquence ), on a ${\displaystyle \sum _{i=0}^{\infty }n_{i}=dN(\nu )}$${\displaystyle dN(\nu )}$${\style d'affichage \nu }$

${\displaystyle {\frac {1}{A}}e^{-1/2h\nu /(kT)}\sum _{i=0}^{\infty }e^{-ih\nu /(kT )}={\frac {1}{A}}e^{-1/2h\nu /(kT)}{\frac {1}{1-e^{-h\nu /(kT)}}} =dN(\nu )}$

D'en haut, nous pouvons obtenir une expression pour 1/A ; en le substituant dans ( 6 ), on a

${\displaystyle dU=dN(\nu )e^{1/2h\nu /(kT)}(1-e^{-h\nu /(kT)})\sum _{i=0}^{\ infty }h\nu (i+1/2)e^{-h\nu (i+1/2)/(kT)}=}$

${\displaystyle =dN(\nu )(1-e^{-h\nu /(kT)})\sum _{i=0}^{\infty }h\nu (i+1/2)e^ {-h\nu i/(kT)}=dN(\nu )h\nu \left({\frac {1}{2}}+(1-e^{-h\nu /(kT)}) \sum _{i=0}^{\infty }ie^{-h\nu i/(kT)}\right)=}$

${\displaystyle dN(\nu )h\nu \left({\frac {1}{2}}+{\frac {1}{e^{h\nu /(kT)}-1}}\right) }$

L'intégration par rapport à ν donne

${\displaystyle U={\frac {9Nh^{4}}{k^{3}T_{\rm {D}}^{3}}}\int _{0}^{\nu _{D}} \left({\frac {1}{2}}+{\frac {1}{e^{h\nu /(kT)}-1}}\right)\nu ^{3}d\nu }$

Limite de basse température

La température d'un solide de Debye est dite basse si , conduisant à ${\displaystyle T\ll T_{\rm {D}}}$

${\displaystyle {\frac {C_{V}}{Nk}}\sim 9\left({T \over T_{\rm {D}}}\right)^{3}\int _{0}^{ \infty }{x^{4}e^{x} \over \left(e^{x}-1\right)^{2}}\,dx}$

Cette intégrale définie peut être évaluée exactement :

${\displaystyle {\frac {C_{V}}{Nk}}\sim {12\pi ^{4} \over 5}\left({T \over T_{\rm {D}}}\right)^ {3}}$

Dans la limite basse température, les limitations du modèle de Debye mentionnées ci-dessus ne s'appliquent pas, et il donne une relation correcte entre la capacité thermique (phononique), la température, les coefficients élastiques et le volume par atome (ces dernières quantités étant contenues dans le Debye température).

Limite de température élevée

La température d'un solide de Debye est dite élevée si . Utiliser si mène à ${\displaystyle T\gg T_{\rm {D}}}$${\displaystyle e^{x}-1\environ x}$${\style d'affichage |x|\ll 1}$

${\displaystyle {\frac {C_{V}}{Nk}}\sim 9\left({T \over T_{\rm {D}}}\right)^{3}\int _{0}^{ T_{\rm {D}}/T}{x^{4} \over x^{2}}\,dx}$

${\displaystyle {\frac {C_{V}}{Nk}}\sim 3\,.}$

C'est la loi de Dulong-Petit , et est assez précise bien qu'elle ne prenne pas en compte l'anharmonicité, ce qui provoque une augmentation supplémentaire de la capacité calorifique. La capacité calorifique totale du solide, s'il est conducteur ou semi - conducteur , peut également contenir une contribution non négligeable des électrons.

Debye contre Einstein

Dans quelle mesure les modèles de Debye et d'Einstein correspondent-ils à l'expérience ? Étonnamment proche, mais Debye est correct à basse température alors qu'Einstein ne l'est pas.

À quel point les modèles sont-ils différents? Pour répondre à cette question, on tracerait naturellement les deux sur le même ensemble d'axes... sauf que l'on ne peut pas. Le modèle d'Einstein et le modèle de Debye fournissent tous deux une forme fonctionnelle pour la capacité calorifique. Ce sont des modèles , et aucun modèle n'est sans échelle. Une échelle relie le modèle à son homologue du monde réel. On peut voir que l'échelle du modèle d'Einstein, qui est donnée par

${\displaystyle C_{V}=3Nk\left({\epsilon \over kT}\right)^{2}{e^{\epsilon /kT} \over \left(e^{\epsilon /kT}-1 \droit)^{2}}}$

est . Et l'échelle du modèle Debye est la température de Debye. Les deux sont généralement trouvés en ajustant les modèles aux données expérimentales. (La température de Debye peut théoriquement être calculée à partir de la vitesse du son et des dimensions du cristal.) Parce que les deux méthodes abordent le problème sous des directions différentes et des géométries différentes, les échelles d'Einstein et de Debye ne sont pas les mêmes, c'est-à-dire ${\displaystyle \epsilon /k}$${\displaystyle T_{\rm {D}}}$

${\displaystyle {\epsilon \over k}\neq T_{\rm {D}}\,,}$

ce qui signifie que les tracer sur le même ensemble d'axes n'a aucun sens. Ce sont deux modèles de la même chose, mais d'échelles différentes. Si l'on définit la température d'Einstein comme

${\displaystyle T_{\rm {E}}\ {\stackrel {\mathrm {def} }{=}}\ {\epsilon \over k}\,,}$

alors on peut dire

${\displaystyle T_{\rm {E}}\neq T_{\rm {D}}\,,}$

et, pour relier les deux, il faut chercher le rapport

${\displaystyle {\frac {T_{\rm {E}}}{T_{\rm {D}}}}=?}$

Le solide d'Einstein est composé d' oscillateurs harmoniques quantiques à fréquence unique , . Cette fréquence, si elle existait effectivement, serait liée à la vitesse du son dans le solide. Si l'on imagine la propagation du son comme une séquence d'atomes se heurtant , alors il devient évident que la fréquence d'oscillation doit correspondre à la longueur d'onde minimale supportée par le réseau atomique, . ${\displaystyle \epsilon =\hbar \omega =h\nu }$${\style d'affichage \lambda _{min}}$

${\displaystyle \nu ={c_{\rm {s}} \over \lambda }={c_{\rm {s}}{\sqrt[{3}]{N}} \over 2L}={c_{ \rm {s}} \over 2}{\sqrt[{3}]{N \over V}}}$

ce qui fait que la température d'Einstein

${\displaystyle T_{\rm {E}}={\epsilon \over k}={h\nu \over k}={hc_{\rm {s}} \over 2k}{\sqrt[{3}] {N \sur V}}\,,}$

et le rapport recherché est donc

${\displaystyle {T_{\rm {E}} \over T_{\rm {D}}}={\sqrt[{3}]{\pi \over 6}}\ =0.805995977...}$

Maintenant, les deux modèles peuvent être tracés sur le même graphique. Notez que ce rapport est la racine cubique du rapport du volume d'un octant d'une sphère tridimensionnelle au volume du cube qui la contient, qui n'est que le facteur de correction utilisé par Debye lors de l'approximation de l'intégrale énergétique ci-dessus.

Alternativement, le rapport des 2 températures peut être considéré comme le rapport de la fréquence unique d'Einstein à laquelle tous les oscillateurs oscillent et la fréquence maximale de Debye. La fréquence unique d'Einstein peut alors être considérée comme une moyenne des fréquences disponibles pour le modèle de Debye.

Tableau des températures de Debye

Même si le modèle de Debye n'est pas tout à fait correct, il donne une bonne approximation de la capacité thermique à basse température des solides cristallins isolants où d'autres contributions (telles que les électrons de conduction très mobiles) sont négligeables. Pour les métaux, la contribution des électrons à la chaleur est proportionnelle à , qui à basse température domine le résultat de Debye pour les vibrations du réseau. Dans ce cas, le modèle de Debye peut seulement être considéré comme approximatif pour la contribution du réseau à la chaleur spécifique. Le tableau suivant répertorie les températures de Debye pour plusieurs éléments purs et saphir : ${\style d'affichage T}$${\displaystyle T^{3}}$

Aluminium 0428 K Béryllium 1440 K Cadmium 0209 K Césium 0038 K Carbone 2230K Chrome 0630 K

Le cuivre 0343 K Germanium 0374 K Or 0170 K Le fer 0470 K Mener 0105 K Manganèse 0410 K

Nickel 0450 K Platine 0240 000 Rubidium 0056 K Saphir 1047 K Sélénium 0090 K Silicium 0645 K

Argent 0215 K Tantale 0240 000 Étain (blanc) 0200 K Titane 0420 K Tungstène 0400 K Zinc 0327 K

L'ajustement du modèle de Debye aux données expérimentales est souvent amélioré d'un point de vue phénoménologique en permettant à la température de Debye de devenir dépendante de la température ; par exemple, la valeur de la glace d'eau augmente d'environ 222 K à 300 K lorsque la température passe du zéro absolu à environ 100 K.

Extension à d'autres quasi-particules

Pour d'autres quasi-particules bosoniques , par exemple pour les magnons (ondes de spin quantifiées) dans les ferroaimants au lieu des phonons (ondes sonores quantifiées), on obtient facilement des résultats analogues. Dans ce cas aux basses fréquences on a des relations de dispersion différentes , par exemple, dans le cas des magnons, au lieu de pour les phonons (avec ). On a également une densité d'états différente (par exemple, ). En conséquence, dans les ferromagnétiques, on obtient une contribution du magnon à la capacité calorifique, , qui domine à des températures suffisamment basses la contribution des phonons, . Dans les métaux, en revanche, la principale contribution à basse température à la capacité calorifique, , provient des électrons. Il est fermions , et est calculé par des méthodes différentes qui remontent à Sommerfeld du modèle d'électron libre . ${\displaystyle E(\nu )\propto k^{2}}$${\style d'affichage E(\nu )\propto k}$${\displaystyle k=2\pi /\lambda }$${\displaystyle \int g(\nu ){\rm {d}}\nu \equiv N\,}$${\displaystyle \Delta C_{\,{\rm {V|\,magnon}}}\,\propto T^{3/2}}$${\displaystyle \,\Delta C_{\,{\rm {V|\,phonon}}}\propto T^{3}}$${\style d'affichage \propto T}$

Extension aux liquides

On a longtemps pensé que la théorie des phonons n'était pas en mesure d'expliquer la capacité calorifique des liquides, car les liquides ne soutiennent que les phonons longitudinaux, mais pas transversaux, qui dans les solides sont responsables des 2/3 de la capacité calorifique. Cependant, des expériences de diffusion Brillouin avec des neutrons et des rayons X , confirmant une intuition de Yakov Frenkel , ont montré que les phonons transversaux existent dans les liquides, bien que limités à des fréquences supérieures à un seuil appelé fréquence de Frenkel . Comme la plupart de l'énergie est contenue dans ces modes à haute fréquence, une simple modification du modèle de Debye est suffisante pour donner une bonne approximation des capacités calorifiques expérimentales de liquides simples.

Fréquence de debye

La fréquence de Debye (symbole : ou ) est un paramètre du modèle de Debye. Il fait référence à une fréquence angulaire de coupure pour les ondes d'une chaîne harmonique de masses, utilisée pour décrire le mouvement des ions dans un réseau cristallin et plus précisément, pour prédire correctement que la capacité calorifique de ces cristaux sera constante pour des températures élevées ( Dulong –Petite loi ). Le terme a été introduit pour la première fois par Peter Debye en 1912. ${\displaystyle \omega _{\rm {Debye}}}$${\displaystyle \omega _{\rm {D}}}$

Tout au long de cet article, des conditions aux limites périodiques sont supposées.

Définition

En supposant que la relation de dispersion est

${\displaystyle \omega =v_{\rm {s}}|\mathbf {k} |}$,

avec la vitesse du son dans le cristal ; et k le vecteur d'onde, la valeur de la fréquence de Debye est la suivante : ${\displaystyle v_{\rm {s}}}$

Pour une chaîne monodimensionnelle, la fréquence de Debye est égale à

${\displaystyle \omega _{\rm {D}}=v_{\rm {s}}\pi /a=v_{\rm {s}}\pi N/L=v_{\rm {s}}\ pi \lambda }$,

avec la distance entre deux atomes voisins dans la chaîne lorsque le système est dans son état fondamental (dans ce cas, cela signifie qu'aucun des atomes ne se déplace l'un par rapport à l'autre) ; le nombre total d'atomes dans la chaîne; et la taille (volume) du système (longueur de la chaîne); et est la densité numérique linéaire . Où la relation suivante est vérifiée : . ${\style d'affichage a}$${\style d'affichage N}$${\style d'affichage L}$${\style d'affichage \lambda }$${\style d'affichage L=Non}$

Pour un réseau carré monoatomique bidimensionnel, la fréquence de Debye est égale à

${\displaystyle \omega _{\rm {D}}^{2}={\frac {4\pi }{a^{2}}}v_{\rm {s}}^{2}={\frac {4\pi N}{A}}v_{\rm {s}}^{2}\equiv 4\pi \sigma v_{\rm {s}}^{2}}$,

où et sont les mêmes qu'avant ; est la taille (surface) de la surface ; et la densité de nombre de surface . ${\style d'affichage a}$${\style d'affichage N}$${\displaystyle A\equiv L^{2}{=}Na^{2}}$${\style d'affichage \sigma }$

Pour un cristal cubique primitif monatomique tridimensionnel , la fréquence de Debye est égale à

${\displaystyle \omega _{\rm {D}}^{3}={\frac {6\pi ^{2}}{a^{3}}}v_{\rm {s}}^{3} ={\frac {6\pi ^{2}N}{V}}v_{\rm {s}}^{3}\equiv 6\pi ^{2}\rho v_{\rm {s}}^ {3}}$,

où et sont les mêmes qu'avant ; la taille du système ; et la densité du nombre de volume . ${\style d'affichage a}$${\style d'affichage N}$${\displaystyle V\equiv L^{3}=Na^{3}}$${\style d'affichage \rho }$

La vitesse du son dans le cristal pourrait dépendre (entre autres) de la masse des atomes, de la force de leur interaction, de la pression sur le système et/ou de la polarisation de l'onde (longitudinale ou transversale), mais dans la suite nous supposerons d'abord que la vitesse du son est la même pour toute polarisation (cette hypothèse n'a cependant pas d'implications de grande envergure).

La relation de dispersion supposée est facilement prouvée fausse pour une chaîne de masses unidimensionnelle, mais dans le modèle de Debye, cela ne s'est pas avéré problématique.

Relation avec la température de Debye

La température de Debye , un autre paramètre du modèle de Debye, est liée à la fréquence de Debye par la relation${\displaystyle \theta _{\rm {D}}}$

${\displaystyle \theta _{\rm {D}}={\frac {\hbar }{k_{\rm {B}}}}\omega _{\rm {D}},}$

où est la constante de Planck réduite et est la constante de Boltzmann . ${\style d'affichage \hbar }$${\displaystyle k_{\rm {B}}}$

Dérivation de Debye

Cristal en trois dimensions

Dans la dérivation de Debye de la capacité calorifique, il additionne tous les modes possibles du système. C'est-à-dire : inclure différentes directions et polarisations . Il a supposé que le nombre total de modes par polarisation était (avec la quantité de masses dans le système), ou en langage mathématique ${\style d'affichage 3N}$${\style d'affichage N}$

${\displaystyle \sum _{\rm {modes}}3=3N}$,

où le des deux côtés est à cause des trois polarisations, donc la somme s'étend sur tous les modes pour une polarisation spécifique. Debye a fait cette hypothèse parce qu'il savait de la mécanique classique que le nombre de modes par polarisation dans une chaîne de masses devrait toujours être égal à la quantité de masses dans la chaîne. ${\style d'affichage 3}$

La partie gauche doit maintenant être explicitée pour montrer comment elle dépend de la fréquence de Debye (ici simplement introduite comme fréquence de coupure, c'est-à-dire : des fréquences plus élevées que la fréquence de Debye ne peuvent pas exister), de sorte qu'une expression pour cela puisse être trouvé.

Tout d'abord, en supposant qu'il soit très grand ( >>1, avec la taille du système dans l'une des trois directions), le vecteur d'onde le plus petit dans n'importe quelle direction pourrait être approximé par : , avec . Des vecteurs d'onde plus petits ne peuvent pas exister en raison des conditions aux limites périodiques . Ainsi la somme deviendrait 4${\style d'affichage L}$${\style d'affichage L}$${\style d'affichage L}$${\displaystyle dk_{i}=2\pi /L}$${\style d'affichage i=x,y,z}$

${\displaystyle \sum _{\rm {modes}}3={\frac {3V}{(2\pi )^{3}}}\iiint d\mathbf {k} }$,

où ; est la taille du système ; et l'intégrale est (comme la sommation) sur tous les modes possibles, qui est supposée être une région finie (limitée par la fréquence de coupure). ${\displaystyle \mathbf {k} \equiv (k_{x},k_{y},k_{z})}$${\displaystyle V\equiv L^{3}}$

L'intégrale triple pourrait être réécrite comme une seule intégrale sur toutes les valeurs possibles de la valeur absolue de (voir : Jacobienne pour les coordonnées sphériques ). Le résultat est ${\displaystyle \mathbf {k} }$

${\displaystyle {\frac {3V}{(2\pi )^{3}}}\iiint d\mathbf {k} ={\frac {3V}{2\pi ^{2}}}\int _{ 0}^{k_{\rm {D}}}|\mathbf {k} |^{2}d\mathbf {k} }$,

avec la valeur absolue du vecteur d'onde correspondant à la fréquence de Debye, donc . ${\displaystyle k_{\rm {D}}}$${\displaystyle k_{\rm {D}}=\omega _{\rm {D}}/v_{\rm {s}}}$

Puisque nous savons que la relation de dispersion est , cela peut être écrit comme une intégrale sur tous les possibles${\displaystyle \omega =v_{\rm {s}}|\mathbf {k} |}$${\displaystyle \omega }$

${\displaystyle {\frac {3V}{2\pi ^{2}}}\int _{0}^{k_{\rm {D}}}|\mathbf {k} |^{2}d\mathbf {k} ={\frac {3V}{2\pi ^{2}v_{\rm {s}}^{3}}}\int _{0}^{\omega _{\rm {D}} }\omega ^{2}d\omega }$,

Après avoir résolu l'intégrale, il est à nouveau égal à pour trouver ${\style d'affichage 3N}$

${\displaystyle {\frac {V}{2\pi ^{2}v_{\rm {s}}^{3}}}\omega _{\rm {D}}^{3}=3N}$.

Conclusion:

${\displaystyle \omega _{\rm {D}}^{3}={\frac {6\pi ^{2}N}{V}}v_{\rm {s}}^{3}}$.

Chaîne à une dimension dans l'espace 3D

La même dérivation pourrait être faite pour une chaîne unidimensionnelle d'atomes. Le nombre de modes reste inchangé, car il y a toujours trois polarisations. Donc

${\displaystyle \sum _{\rm {modes}}3=3N}$.

Le reste de la dérivation est analogue à la précédente, donc encore une fois le côté gauche est réécrit ;

${\displaystyle \sum _{\rm {modes}}3={\frac {3L}{2\pi }}\int _{-k_{\rm {D}}}^{k_{\rm {D} }}dk={\frac {3L}{\pi v_{\rm {s}}}}\int _{0}^{\omega _{\rm {D}}}d\omega }$.

Dans la dernière étape, la multiplication par deux est négative, mais pas. Nous continuons; ${\style d'affichage k}$${\displaystyle \omega }$

${\displaystyle {\frac {3L}{\pi v_{\rm {s}}}}\int _{0}^{\omega _{\rm {D}}}d\omega ={\frac {3L }{\pi v_{\rm {s}}}}\omega _{\rm {D}}=3N}$.

Conclusion:

${\displaystyle \omega _{\rm {D}}={\frac {\pi v_{\rm {s}}N}{L}}}$.

Cristal bidimensionnel

La même dérivation pourrait être faite pour un cristal à deux dimensions. Encore une fois, le nombre de modes reste inchangé, car il y a toujours trois polarisations. La dérivation est analogue aux deux précédentes. On part de la même équation,

${\displaystyle \sum _{\rm {modes}}3=3N}$.

Et puis le côté gauche est réécrit et assimilé à ${\style d'affichage 3N}$

${\displaystyle \sum _{\rm {modes}}3={\frac {3A}{(2\pi )^{2}}}\iint d\mathbf {k} ={\frac {3A}{2 \pi v_{\rm {s}}^{2}}}\int _{0}^{\omega _{\rm {D}}}\omega d\omega ={\frac {3A\omega _{ \rm {D}}^{2}}{4\pi v_{\rm {s}}^{2}}}=3N}$,

où est la taille du système. ${\displaystyle A\equiv L^{2}}$

Conclusion

${\displaystyle \omega _{\rm {D}}^{2}={\frac {4\pi N}{A}}v_{\rm {s}}^{2}}$.

Permettre à la polarisation de faire la différence

Comme mentionné dans l'introduction : en général, les ondes longitudinales ont une vitesse d'onde différente de celle des ondes transversales. Pour plus de clarté, ils ont d'abord été supposés être égaux, mais maintenant nous abandonnons cette hypothèse.

La relation de dispersion devient , où , qui correspondent aux trois polarisations. La fréquence de coupure (fréquence Debye) ne dépend cependant pas de . Et nous pouvons écrire le nombre total de modes sous la forme , qui est à nouveau égal à . Ici, la sommation sur les modes est (bien que non explicitement indiquée) dépendante de . ${\displaystyle \omega _{i}=v_{s,i}|\mathbf {k} |}$${\style d'affichage i=1,2,3}$${\style d'affichage i}$${\displaystyle \sum _{i}\sum _{\rm {modes}}1}$${\style d'affichage 3N}$${\style d'affichage i}$

Une dimension

Une fois de plus la sommation sur les modes est réécrite

${\displaystyle \sum _{i}\sum _{\rm {modes}}1=\sum _{i}{\frac {L}{\pi v_{s,i}}}\int _{0} ^{\omega _{\rm {D}}}d\omega _{i}=3N}$.

Le résultat est

${\displaystyle {\frac {L\omega _{\rm {D}}}{\pi }}({\frac {1}{v_{s,1}}}+{\frac {1}{v_{ s,2}}}+{\frac {1}{v_{s,3}}})=3N}$.

On trouve ainsi la fréquence de Debye

${\displaystyle \omega _{\rm {D}}={\frac {3\pi N}{L}}{\frac {v_{s,1}v_{s,2}v_{s,3}} {v_{s,2}v_{s,3}+v_{s,1}v_{s,3}+v_{s,1}v_{s,2}}}}$.

Soit en supposant que les deux polarisations transversales sont identiques (pour avoir la même vitesse de phase et la même fréquence)

${\displaystyle \omega _{\rm {D}}={\frac {3\pi N}{L}}{\frac {v_{s,t}^{2}v_{s,l}}{2v_ {s,t}v_{s,l}+v_{s,t}^{2}}}}$.

On peut vérifier que cette relation est équivalente à celle trouvée précédemment (lorsque la polarisation ne faisait pas de différence) en réglant . ${\displaystyle v_{s,t}=v_{s,l}}$

Deux dimensions

La même dérivation peut être effectuée pour un cristal bidimensionnel à trouver (la dérivation est analogue aux dérivations précédentes)

${\displaystyle \omega _{\rm {D}}^{2}={\frac {12\pi N}{A}}{\frac {(v_{s,1}v_{s,2}v_{ s,3})^{2}}{(v_{s,2}v_{s,3})^{2}+(v_{s,1}v_{s,3})^{2}+( v_{s,1}v_{s,2})^{2}}}}$.

Ou en supposant que les deux polarisations transversales sont égales (bien que pour deux dimensions il serait plus logique que toutes les polarisations soient différentes) :

${\displaystyle \omega _{\rm {D}}^{2}={\frac {12\pi N}{A}}{\frac {(v_{s,t}^{2}v_{s, l})^{2}}{2(v_{s,t}v_{s,l})^{2}+v_{s,t}^{4}}}}$.

Encore une fois, on peut vérifier que cette relation est équivalente à celle trouvée précédemment en définissant . ${\displaystyle v_{s,t}=v_{s,l}}$

Trois dimensions

La même dérivation peut être effectuée pour un cristal tridimensionnel à trouver (la dérivation est analogue aux dérivations précédentes)

${\displaystyle \omega _{\rm {D}}^{3}={\frac {18\pi ^{2}N}{V}}{\frac {(v_{s,1}v_{s, 2}v_{s,3})^{3}}{(v_{s,2}v_{s,3})^{3}+(v_{s,1}v_{s,3})^{ 3}+(v_{s,1}v_{s,2})^{3}}}}$.

Ou en supposant que les deux polarisations transversales sont égales (bien que pour trois dimensions ce serait plus logique quand toutes les polarisations seraient les mêmes) :

${\displaystyle \omega _{\rm {D}}^{3}={\frac {18\pi ^{2}N}{V}}{\frac {(v_{s,t}^{2} v_{s,l})^{3}}{2(v_{s,t}v_{s,l})^{3}+v_{s,t}^{6}}}}$.

Encore une fois, on peut vérifier que cette relation est équivalente à celle trouvée précédemment en définissant . ${\displaystyle v_{s,t}=v_{s,l}}$

Dérivation avec la relation de dispersion réelle

Ce problème pourrait être rendu plus perspicace en le rendant plus complexe. Au lieu d'utiliser la relation de dispersion , la relation de dispersion correcte va maintenant être supposée. De la mécanique classique, il est connu que pour une chaîne équidistante de masses qui interagissent harmoniquement les unes avec les autres, la relation de dispersion se lit comme suit ${\displaystyle \omega =v_{\rm {s}}k}$

${\displaystyle \omega (k)=2{\sqrt {\frac {\kappa }{m}}}\left|\sin \left({\frac {ka}{2}}\right)\right|}$.

Après avoir tracé cette relation, il est clair que l'estimation de Debye de la longueur d'onde de coupure était juste après tout. Parce que pour chaque nombre d'onde plus grand que (c'est-à-dire : est plus petit que ) un nombre d'onde qui est plus petit que ce qui pourrait être trouvé avec la même fréquence angulaire. Cela signifie que la manifestation physique résultante pour le mode avec le plus grand nombre d'ondes est indiscernable de celui avec le plus petit nombre d'ondes. De ce fait, l'étude de la relation de dispersion peut être limitée à la première zone de brillouin c'est-à-dire pour . Ceci est possible car le système est constitué de points discrétisés , comme le montre l'image animée. En divisant la relation de dispersion par et en insérant pour , nous trouvons la vitesse d'une onde avec à être ${\style d'affichage \pi /a}$${\style d'affichage \lambda }$${\style d'affichage 2a}$${\style d'affichage \pi /a}$${\displaystyle k\in [-{\frac {\pi }{a}},{\frac {\pi }{a}}]}$${\style d'affichage k}$${\style d'affichage \pi /a}$${\style d'affichage k}$${\displaystyle k=\pi /a}$

${\displaystyle v_{\rm {s}}(k=\pi /a)={\frac {2}a}{\pi }}{\sqrt {\frac {\kappa }{m}}}}$.

En insérant simplement dans la relation de dispersion d'origine, nous trouvons ${\displaystyle k=\pi /a}$

${\displaystyle \omega (k=\pi /a)=2{\sqrt {\frac {\kappa }{m}}}=\omega _{\rm {D}}}$.

En combinant ces résultats, le même résultat est à nouveau trouvé

${\displaystyle \omega _{\rm {D}}={\frac {\pi v_{\rm {s}}}{a}}}$.

Cependant, pour les chaînes diatomiques (et les chaînes plus complexes) la fréquence de coupure (et la longueur d'onde) associée n'est pas très précise, car la longueur d'onde de coupure est deux fois plus grande et la relation de dispersion est constituée de deux branches (pour une chaîne diatomique) . Il n'est pas non plus certain à partir de cela que pour les systèmes plus dimensionnels, la fréquence de coupure ait été prédite avec précision par Debye.

Dérivation alternative

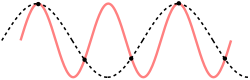
Pour une chaîne unidimensionnelle, ce résultat pourrait également être reproduit en utilisant la théorie du repliement. Le théorème d'échantillonnage de Nyquist-Shannon est utilisé dans la dérivation suivante; la principale différence étant que dans la dérivation suivante la discrétisation n'est pas dans le temps, mais dans l'espace. Si nous utilisons la relation de dispersion correcte du dernier paragraphe, il sera clair d'une autre manière perspicace pourquoi la fréquence de coupure a la valeur précédemment (deux fois) dérivée. Donc encore,

${\displaystyle \omega (k)=2{\sqrt {\frac {\kappa }{m}}}\left|\sin \left({\frac {ka}{2}}\right)\right|}$

est assumé.

Cette dérivation est tout à fait équivalente à la précédente, c'est-à-dire que les mêmes hypothèses sont faites pour récupérer le résultat. Ce n'est pas plus ou moins précis, c'est juste une approche différente.

Pour déterminer où doit être la fréquence de coupure, il est utile de déterminer d'abord où doit être la coupure de la longueur d'onde. De la relation de dispersion, nous savons que pour chaque mode est répété, donc la longueur d'onde de coupure serait à . À partir de cela et des conditions aux limites périodiques, vous pouvez immédiatement voir que le nombre total de modes par polarisation serait de . Comme on le voit dans le gif du paragraphe précédent, c'est parce que chaque onde avec une longueur d'onde plus courte que pourrait être remplacée par une onde avec une longueur d'onde plus longue que pour retrouver le même résultat physique. ${\displaystyle k>\pi /a}$${\displaystyle \lambda _{\rm {D}}=2a}$${\style d'affichage N}$${\style d'affichage 2a}$${\style d'affichage 2a}$

Cependant, la relation de dispersion du paragraphe précédent (la bonne) n'est même pas nécessaire pour expliquer pourquoi la coupure devrait être à . Parce que, comme cela est représenté, seules les ondes avec une longueur d'onde plus longue que celles qui pourraient donner le même résultat physique qu'une autre. C'est donc une autre façon de prédire correctement la longueur d'onde de coupure sans utiliser la relation de dispersion correcte (ou même les connaissances de la mécanique classique comme l'a fait Debye). Cependant, en utilisant la mauvaise relation de dispersion supposée par Debye, les ondes avec une longueur d'onde plus petite auraient une fréquence plus élevée, mais le mouvement relatif des masses serait le même, donc cela ne rend pas de nouveaux modes. ${\style d'affichage \lambda =1a}$${\style d'affichage 2a}$

Cela se traduit à nouveau par , le rendu ${\displaystyle k_{\rm {D}}=\pi /a}$

${\displaystyle \omega _{\rm {D}}={\frac {\pi v_{\rm {s}}}{a}}}$.

Ici aussi, peu importe la relation de dispersion utilisée (la bonne ou celle de Debye utilisée), la même fréquence de coupure serait trouvée.

Malheureusement, la même méthode n'a pas pu être utilisée (aussi facilement) pour un cristal à deux ou trois dimensions, car les ondes diagonales auraient une longueur d'onde de coupure plus grande, ce qui est également difficile à prévoir.

Voir également

• Gaz Bose
• Gaz dans une boîte
• Paramètre Grüneisen

Les références

Lectures complémentaires

• CRC Handbook of Chemistry and Physics , 56e édition (1975-1976)
• Schroeder, Daniel V. Une introduction à la physique thermique . Addison-Wesley, San Francisco (2000). Article 7.5.

Liens externes

• Détermination expérimentale de la chaleur spécifique, de la conductivité thermique et thermique du quartz à l'aide d'un cryostat.
• Simon, Steven H. (2014) The Oxford Solid State Basics (les plus pertinents : 1, 2 et 6)