Modèle d'électrons libres - Free electron model

En physique du solide , le modèle des électrons libres est un modèle de mécanique quantique pour le comportement des porteurs de charge dans un solide métallique . Il a été développé en 1927, principalement par Arnold Sommerfeld , qui a combiné le modèle classique de Drude avec les statistiques de Fermi-Dirac de mécanique quantique et est donc également connu sous le nom de modèle Drude-Sommerfeld .

Compte tenu de sa simplicité, il réussit étonnamment bien à expliquer de nombreux phénomènes expérimentaux, en particulier

• la loi de Wiedemann-Franz qui relie la conductivité électrique et la conductivité thermique ;
• la dépendance à la température de la capacité thermique des électrons ;
• la forme de la densité d'états électronique ;
• la gamme des valeurs d'énergie de liaison ;
• conductivités électriques;
• le coefficient Seebeck de l' effet thermoélectrique ;
• émission thermique d'électrons et émission électronique de champ à partir de métaux en vrac

Le modèle des électrons libres a résolu de nombreuses incohérences liées au modèle de Drude et a donné un aperçu de plusieurs autres propriétés des métaux. Le modèle des électrons libres considère que les métaux sont composés d'un gaz d'électrons quantique où les ions ne jouent quasiment aucun rôle. Le modèle peut être très prédictif lorsqu'il est appliqué aux métaux alcalins et nobles .

Idées et hypothèses

Dans le modèle à électrons libres, quatre hypothèses principales sont prises en compte :

• Approximation des électrons libres : L'interaction entre les ions et les électrons de valence est généralement négligée, sauf dans les conditions aux limites. Les ions ne gardent que la neutralité de charge dans le métal. Contrairement au modèle Drude, les ions ne sont pas forcément à l'origine des collisions.
• Approximation électronique indépendante : Les interactions entre électrons sont ignorées. Les champs électrostatiques dans les métaux sont faibles en raison de l' effet écran .
• Approximation du temps de relaxation : Il existe un mécanisme de diffusion inconnu tel que la probabilité de collision des électrons est inversement proportionnelle au temps de relaxation , qui représente le temps moyen entre les collisions. Les collisions ne dépendent pas de la configuration électronique.${\style d'affichage \tau }$
• Principe d'exclusion de Pauli : Chaque état quantique du système ne peut être occupé que par un seul électron. Cette restriction des états électroniques disponibles est prise en compte par les statistiques de Fermi-Dirac (voir aussi Gaz de Fermi ). Les principales prédictions du modèle à électrons libres sont dérivées du développement de Sommerfeld de l'occupation de Fermi-Dirac pour les énergies autour du niveau de Fermi .

Le nom du modèle vient des deux premières hypothèses, car chaque électron peut être traité comme une particule libre avec une relation quadratique respective entre énergie et quantité de mouvement.

Le réseau cristallin n'est pas explicitement pris en compte dans le modèle des électrons libres, mais une justification de la mécanique quantique est donnée un an plus tard (1928) par le théorème de Bloch : un électron non lié se déplace dans un potentiel périodique comme un électron libre dans le vide, sauf pour la masse électronique m _e devenant une masse effective m* qui peut s'écarter considérablement de m _e (on peut même utiliser une masse effective négative pour décrire la conduction par trous d'électrons ). Les masses effectives peuvent être dérivées de calculs de structure de bande qui n'ont pas été initialement pris en compte dans le modèle d'électrons libres.

Du modèle Drude

De nombreuses propriétés physiques découlent directement du modèle de Drude , car certaines équations ne dépendent pas de la distribution statistique des particules. Prendre la distribution de vitesse classique d'un gaz parfait ou la distribution de vitesse d'un gaz de Fermi ne change que les résultats liés à la vitesse des électrons.

Principalement, le modèle d'électron libre et le modèle de Drude prédisent le même courant continu conductivité électrique σ pour la loi d'Ohm , qui est

${\displaystyle \mathbf {J} =\sigma \mathbf {E} \quad }$ avec ${\displaystyle \quad \sigma ={\frac {ne^{2}\tau }{m_{e}}},}$

où est la densité de courant , est le champ électrique externe, est la densité électronique (nombre d'électrons/volume), est le temps libre moyen et est la charge électrique des électrons . ${\displaystyle \mathbf {J} }$${\displaystyle \mathbf {E} }$${\style d'affichage n}$${\style d'affichage \tau }$${\style d'affichage e}$

D'autres quantités qui restent les mêmes sous le modèle des électrons libres que sous celui de Drude sont la susceptibilité AC, la fréquence du plasma , la magnétorésistance et le coefficient Hall lié à l' effet Hall .

Propriétés d'un gaz d'électrons

De nombreuses propriétés du modèle des électrons libres découlent directement des équations liées au gaz de Fermi, car l'approximation des électrons indépendants conduit à un ensemble d'électrons sans interaction. Pour un gaz d'électrons tridimensionnel, nous pouvons définir l' énergie de Fermi comme

${\displaystyle E_{\rm {F}}={\frac {\hbar ^{2}}{2m_{e}}}\left(3\pi ^{2}n\right)^{\frac {2 }{3}},}$

où est la constante de Planck réduite . L' énergie de Fermi définit l'énergie de l'électron d'énergie la plus élevée à température nulle. Pour les métaux, l'énergie de Fermi est de l'ordre des unités d' électronvolts au-dessus de l'énergie minimale de la bande d'électrons libres. ${\style d'affichage \hbar }$

En trois dimensions, la densité d'états d'un gaz de fermions est proportionnelle à la racine carrée de l'énergie cinétique des particules.

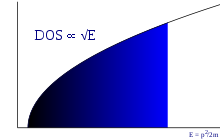
Densité d'états

La densité d'états 3D (nombre d'états énergétiques, par énergie par volume) d'un gaz d'électrons sans interaction est donnée par :

${\displaystyle g(E)={\frac {m_{e}}{\pi ^{2}\hbar ^{3}}}{\sqrt {2m_{e}E}}={\frac {3} {2}}{\frac {n}{E_{\rm {F}}}}{\sqrt {\frac {E}{E_{\rm {F}}}}},}$

où est l'énergie d'un électron donné. Cette formule prend en compte la dégénérescence du spin mais ne considère pas un éventuel décalage d'énergie dû au bas de la bande de conduction . Pour 2D, la densité d'états est constante et pour 1D est inversement proportionnelle à la racine carrée de l'énergie des électrons. ${\textstyle E\geq 0}$

Niveau de Fermi

Le potentiel chimique des électrons dans un solide est également connu sous le nom de niveau de Fermi et, comme l' énergie de Fermi connexe , souvent noté . L' expansion de Sommerfeld peut être utilisée pour calculer le niveau de Fermi ( ) à des températures plus élevées comme : ${\style d'affichage \mu }$${\displaystyle E_{\rm {F}}}$${\style d'affichage T>0}$

${\displaystyle E_{\rm {F}}(T)=E_{\rm {F}}(T=0)\left[1-{\frac {\pi ^{2}}{12}}\left ({\frac {T}{T_{\rm {F}}}}\right)^{2}-{\frac {\pi ^{4}}{80}}\left({\frac {T} {T_{\rm {F}}}}\right)^{4}+\cdots \right],}$

où est la température et nous définissons comme la température de Fermi ( est la constante de Boltzmann ). L'approche perturbative est justifiée car la température de Fermi est généralement de l'ordre de 10 ⁵ K pour un métal, donc à température ambiante ou inférieure l'énergie de Fermi et le potentiel chimique sont pratiquement équivalents. ${\style d'affichage T}$${\textstyle T_{\rm {F}}=E_{\rm {F}}/k_{\rm {B}}}$${\displaystyle k_{\rm {B}}}$${\style d'affichage E_{\rm {F}}(T=0)}$${\displaystyle E_{\rm {F}}(T>0)}$

Compressibilité des métaux et pression de dégénérescence

L'énergie totale par unité de volume (at ) peut également être calculée en intégrant sur l' espace des phases du système, nous obtenons ${\styletexte T=0}$

${\displaystyle u(0)={\frac {3}{5}}nE_{\rm {F}},}$

qui ne dépend pas de la température. Comparez avec l'énergie par électron d'un gaz parfait : , qui est nulle à température nulle. Pour qu'un gaz parfait ait la même énergie que le gaz d'électrons, les températures devraient être de l'ordre de la température de Fermi. Thermodynamiquement, cette énergie du gaz d'électrons correspond à une pression à température nulle donnée par ${\textstyle {\frac {3}{2}}k_{\rm {B}}T}$

${\displaystyle P=-\left({\frac {\partial U}{\partial V}}\right)_{T,\mu }={\frac {2}{3}}u(0),}$

où est le volume et est l'énergie totale, la dérivée effectuée à température et à potentiel chimique constant. Cette pression est appelée pression de dégénérescence des électrons et ne provient pas de la répulsion ou du mouvement des électrons mais de la restriction selon laquelle pas plus de deux électrons (en raison des deux valeurs de spin) peuvent occuper le même niveau d'énergie. Cette pression définit la compressibilité ou module de compression du métal ${\textstyle V}$${\styletexte U(T)=u(T)V}$

${\displaystyle B=-V\left({\frac {\partial P}{\partial V}}\right)_{T,\mu }={\frac {5}{3}}P={\frac {2}{3}}nE_{\rm {F}}.}$

Cette expression donne le bon ordre de grandeur pour le module de masse pour les métaux alcalins et les métaux nobles, ce qui montre que cette pression est aussi importante que d'autres effets à l'intérieur du métal. Pour les autres métaux, la structure cristalline doit être prise en compte.

Prédictions supplémentaires

Capacité thermique

Un problème ouvert en physique du solide avant l'arrivée du modèle des électrons libres était lié à la faible capacité calorifique des métaux. Même lorsque le modèle de Drude était une bonne approximation du nombre de Lorenz de la loi de Wiedemann-Franz, l'argument classique est basé sur l'idée que la capacité calorifique volumétrique d'un gaz parfait est

${\displaystyle c_{V}^{\text{Drude}}={\frac {3}{2}}nk_{\rm {B}}}$.

Si tel était le cas, la capacité calorifique d'un métal pourrait être beaucoup plus élevée en raison de cette contribution électronique. Néanmoins, une si grande capacité calorifique n'a jamais été mesurée, ce qui soulève des soupçons sur l'argument. En utilisant le développement de Sommerfeld, on peut obtenir des corrections de la densité d'énergie à température finie et obtenir la capacité thermique volumétrique d'un gaz d'électrons, donnée par :

${\displaystyle c_{V}=\left({\frac {\partial u}{\partial T}}\right)_{n}={\frac {\pi ^{2}}{2}}{\ frac {T}{T_{\rm {F}}}}nk_{\rm {B}}}$,

où le préfacteur to est considérablement plus petit que le 3/2 trouvé dans , environ 100 fois plus petit à température ambiante et beaucoup plus petit à basse . La bonne estimation du nombre de Lorenz dans le modèle de Drude était le résultat de la vitesse moyenne classique de l'électron étant environ 100 plus grande que la version quantique, compensant la grande valeur de la capacité thermique classique. Le calcul du modèle d'électrons libres du facteur de Lorenz est environ le double de la valeur de Drude et est plus proche de la valeur expérimentale. Avec cette capacité thermique, le modèle à électrons libres est également capable de prédire le bon ordre de grandeur et la dépendance à la température à faible T pour le coefficient Seebeck de l' effet thermoélectrique . ${\displaystyle nk_{B}}$${\textstyle c_{V}^{\text{Drude}}}$${\textstyle T}$

Évidemment, la contribution électronique seule ne prédit pas la loi de Dulong-Petit , c'est-à-dire l'observation que la capacité calorifique d'un métal est constante à haute température. Le modèle des électrons libres peut être amélioré dans ce sens en ajoutant la contribution des vibrations du réseau. Deux schémas célèbres pour inclure le réseau dans le problème sont le modèle solide d'Einstein et le modèle de Debye . Avec l'ajout de ce dernier, la capacité calorifique volumétrique d'un métal à basse température peut être plus précisément écrite sous la forme,

${\displaystyle c_{V}\approx \gamma T+AT^{3}}$,

où et sont des constantes liées au matériau. Le terme linéaire vient de la contribution électronique tandis que le terme cubique vient du modèle de Debye. A haute température cette expression n'est plus correcte, la capacité calorifique électronique peut être négligée, et la capacité calorifique totale du métal tend vers une constante. ${\style d'affichage \gamma }$${\style d'affichage A}$

Voie libre moyenne

Notez que sans l'approximation du temps de relaxation, il n'y a aucune raison pour que les électrons dévient leur mouvement, car il n'y a pas d'interactions, donc le libre parcours moyen devrait être infini. Le modèle de Drude considérait que le libre parcours moyen des électrons était proche de la distance entre les ions dans le matériau, ce qui implique la conclusion précédente que le mouvement de diffusion des électrons était dû à des collisions avec les ions. Les chemins libres moyens dans le modèle d'électrons libres sont plutôt donnés par (où est la vitesse de Fermi) et sont de l'ordre de centaines d' ångströms , au moins un ordre de grandeur plus grand que tout calcul classique possible. Le libre parcours moyen n'est alors pas le résultat de collisions électron-ion mais est plutôt lié à des imperfections du matériau, soit dues à des défauts et des impuretés dans le métal, soit à des fluctuations thermiques. ${\textstyle \lambda =v_{\rm {F}}\tau }$${\textstyle v_{\rm {F}}={\sqrt {2E_{\rm {F}}/m_{e}}}}$

Inexactitudes et extensions

Le modèle des électrons libres présente plusieurs insuffisances qui sont contredites par l'observation expérimentale. Nous énumérons quelques inexactitudes ci-dessous :

Dépendance à la température

Le modèle des électrons libres présente plusieurs quantités physiques qui ont une mauvaise dépendance à la température, ou aucune dépendance du tout comme la conductivité électrique. La conductivité thermique et la chaleur spécifique sont bien prédites pour les métaux alcalins à basse température, mais ne permettent pas de prédire le comportement à haute température provenant du mouvement des ions et de la diffusion des phonons .

Effet Hall et magnétorésistance

Le coefficient de Hall a une valeur constante R _H = –1/( ne ) dans le modèle de Drude et dans le modèle des électrons libres. Cette valeur est indépendante de la température et de l'intensité du champ magnétique. Le coefficient de Hall dépend en fait de la structure de la bande et la différence avec le modèle peut être assez dramatique lorsqu'on étudie des éléments comme le magnésium et l' aluminium qui ont une forte dépendance au champ magnétique. Le modèle des électrons libres prédit également que la magnétorésistance transversale, la résistance dans le sens du courant, ne dépend pas de la force du champ. Dans presque tous les cas, c'est le cas.

Directionnel

La conductivité de certains métaux peut dépendre de l'orientation de l'échantillon par rapport au champ électrique. Parfois même le courant électrique n'est pas parallèle au champ. Cette possibilité n'est pas décrite car le modèle n'intègre pas la cristallinité des métaux, c'est-à-dire l'existence d'un réseau périodique d'ions.

Diversité dans la conductivité

Tous les matériaux ne sont pas conducteurs électriques , certains ne conduisent pas très bien l'électricité ( isolants ), certains peuvent conduire lorsque des impuretés sont ajoutées comme les semi-conducteurs . Des semi - métaux , à bandes de conduction étroites existent également. Cette diversité n'est pas prédite par le modèle et ne peut être expliquée qu'en analysant les bandes de valence et de conduction . De plus, les électrons ne sont pas les seuls porteurs de charge dans un métal, des lacunes ou des trous d' électrons peuvent être considérés comme des quasi-particules portant une charge électrique positive. La conduction des trous conduit à un signe opposé pour les coefficients de Hall et Seebeck prédits par le modèle.

D'autres insuffisances sont présentes dans la loi de Wiedemann-Franz aux températures intermédiaires et la dépendance en fréquence des métaux dans le spectre optique.

Des valeurs plus exactes pour la conductivité électrique et la loi de Wiedemann-Franz peuvent être obtenues en adoucissant l'approximation du temps de relaxation en faisant appel aux équations de transport de Boltzmann ou à la formule de Kubo .

Le spin est largement négligé dans le modèle des électrons libres et ses conséquences peuvent conduire à des phénomènes magnétiques émergents comme le paramagnétisme de Pauli et le ferromagnétisme .

Une continuation immédiate du modèle d'électrons libres peut être obtenue en supposant l' approximation de réseau vide , qui constitue la base du modèle de structure de bande connu sous le nom de modèle d'électrons presque libres .

L'ajout d'interactions répulsives entre électrons ne change pas beaucoup le tableau présenté ici. Lev Landau a montré qu'un gaz de Fermi sous interactions répulsives, peut être vu comme un gaz de quasiparticules équivalentes qui modifient légèrement les propriétés du métal. Le modèle de Landau est maintenant connu sous le nom de théorie du liquide de Fermi . Des phénomènes plus exotiques comme la supraconductivité , où les interactions peuvent être attractives, nécessitent une théorie plus affinée.

Voir également

• Le théorème de Bloch
• Entropie électronique
• Liaison étroite
• Gaz d'électrons bidimensionnel
• Statistiques Bose-Einstein
• surface Fermi
• nain blanc

Les références

Général

• Kittel, Charles (1953). Introduction à la physique du solide . Université du Michigan : Wiley.
• Ashcroft, Neil ; Mermin, N. David (1976). Physique du Solide . New York : Holt, Rinehart et Winston. ISBN 978-0-03-083993-1.
• Sommerfeld, Arnold ; Bethe, Hans (1933). Elektronentheorie der Metalle . Berlin Heidelberg : Springer Verlag. ISBN 978-3642950025.