Théorie des contraintes infinitésimales - Infinitesimal strain theory

Fait partie d'une série sur
Mécanique des milieux continus
${\displaystyle J=-D{\frac {d\varphi }{dx}}}$ Les lois de diffusion de Fick
Lois Conservations Masse Élan Énergie Inégalités Clausius-Duhem (entropie)
Mécanique solide Déformation Élasticité linéaire Plasticité la loi de Hooke Stress Souche finie Souche infinitésimale Compatibilité Pliant Contacter les mécaniciens frictionnel Théorie de la défaillance matérielle Mécanique des fractures
Mécanique des fluides Fluides Statique  · Dynamique Principe d'Archimède  · Principe de Bernoulli Équations de Navier-Stokes Équation de Poiseuille  · Loi de Pascal Viscosité ( newtonien  · non newtonien ) Flottabilité  · Mélange  · Pression Liquides Adhésion Capillarité Chromatographie Cohésion (chimie) Tension superficielle Des gaz Atmosphère la loi de Boyle la loi de Charles Loi sur les gaz combinés La loi de Fick La loi Gay-Lussac la loi de Graham Plasma
Rhéologie Viscoélasticité Rhéométrie Rhéomètre Fluides intelligents Électrorhéologique Magnétorhéologique Ferrofluides
Scientifiques Bernoulli Boyle Cauchy Charles Euler Baise Gay-Lussac Graham Hooke Newton Navire Noll Pascal Stokes Truesdell
v t e

En mécanique des milieux continus , la théorie des déformations infinitésimales est une approche mathématique de la description de la déformation d'un corps solide dans laquelle les déplacements des particules matérielles sont supposés être beaucoup plus petits (en fait, infiniment plus petits) que toute dimension pertinente du corps; de sorte que sa géométrie et les propriétés constitutives du matériau (telles que la densité et la rigidité ) à chaque point de l'espace peuvent être supposées inchangées par la déformation.

Avec cette hypothèse, les équations de la mécanique des milieux continus sont considérablement simplifiées. Cette approche peut également être appelée théorie des petites déformations , petite théorie de déplacement , ou petite théorie déplacement à gradient . Elle est opposée à la théorie des déformations finies où l'hypothèse opposée est faite.

La théorie des déformations infinitésimales est couramment adoptée en génie civil et mécanique pour l' analyse des contraintes des structures construites à partir de matériaux élastiques relativement rigides comme le béton et l' acier , car un objectif commun dans la conception de telles structures est de minimiser leur déformation sous des charges typiques . Cependant, cette approximation demande de la prudence dans le cas de corps souples minces, tels que des tiges, des plaques et des coques qui sont susceptibles de rotations importantes, rendant ainsi les résultats peu fiables.

Tenseur de déformation infinitésimal

Pour les déformations infinitésimales d'un corps continu , dans lequel le gradient de déplacement (tenseur d'ordre 2) est petit par rapport à l'unité, c'est-à-dire qu'il est possible d'effectuer une linéarisation géométrique de l'un des (infiniment nombreux possibles) tenseurs de déformation utilisés en déformation finie théorie, par exemple le tenseur de déformation lagrangien , et le tenseur de déformation eulérien . Dans une telle linéarisation, les termes non linéaires ou du second ordre du tenseur de déformation fini sont négligés. Ainsi nous avons ${\displaystyle \|\nabla \mathbf {u} \|\ll 1}$${\displaystyle \mathbf {E} }$${\displaystyle \mathbf {e} }$

${\displaystyle \mathbf {E} ={\frac {1}{2}}\left(\nabla _{\mathbf {X} }\mathbf {u} +(\nabla _{\mathbf {X} }\ mathbf {u} )^{T}+(\nabla _{\mathbf {X} }\mathbf {u} )^{T}\nabla _{\mathbf {X} }\mathbf {u} \right)\ approx {\frac {1}{2}}\gauche(\nabla _{\mathbf {X} }\mathbf {u} +(\nabla _{\mathbf {X} }\mathbf {u} )^{T }\droit)}$

ou

${\displaystyle E_{KL}={\frac {1}{2}}\left({\frac {\partial U_{K}}{\partial X_{L}}}+{\frac {\partial U_{ L}}{\partial X_{K}}}+{\frac {\partial U_{M}}{\partial X_{K}}}{\frac {\partial U_{M}}{\partial X_{L }}}\right)\approx {\frac {1}{2}}\left({\frac {\partial U_{K}}{\partial X_{L}}}+{\frac {\partial U_{ L}}{\partiel X_{K}}}\right)}$

et

${\displaystyle \mathbf {e} ={\frac {1}{2}}\left(\nabla _{\mathbf {x} }\mathbf {u} +(\nabla _{\mathbf {x} }\ mathbf {u} )^{T}-\nabla _{\mathbf {x} }\mathbf {u} (\nabla _{\mathbf {x} }\mathbf {u} )^{T}\right)\ approx {\frac {1}{2}}\gauche(\nabla _{\mathbf {x} }\mathbf {u} +(\nabla _{\mathbf {x} }\mathbf {u} )^{T }\droit)}$

ou

${\displaystyle e_{rs}={\frac {1}{2}}\left({\frac {\partial u_{r}}{\partial x_{s}}}+{\frac {\partial u_{ s}}{\partial x_{r}}}-{\frac {\partial u_{k}}{\partial x_{r}}}{\frac {\partial u_{k}}{\partial x_{s }}}\right)\approx {\frac {1}{2}}\left({\frac {\partial u_{r}}{\partial x_{s}}}+{\frac {\partial u_{ s}}{\partiel x_{r}}}\right)}$

Cette linéarisation implique que la description lagrangienne et la description eulérienne sont approximativement les mêmes car il y a peu de différence dans les coordonnées matérielles et spatiales d'un point matériel donné dans le continuum. Par conséquent, les composantes du gradient de déplacement matériel et les composantes du gradient de déplacement spatial sont approximativement égales. Ainsi nous avons

$${\displaystyle \mathbf {E} \approx \mathbf {e} \approx {\boldsymbol {\varepsilon }}={\frac {1}{2}}\left((\nabla \mathbf {u} )^{ T}+\nabla \mathbf {u} \right)}$$

$${\displaystyle E_{KL}\approx e_{rs}\approx \varepsilon _{ij}={\frac {1}{2}}\left(u_{i,j}+u_{j,i}\right )}$$

où sont les composantes du tenseur des déformations de infinitésimale , également appelé le tenseur des déformations de Cauchy , tenseur de déformation linéaire ou petit tenseur des déformations . ${\displaystyle \varepsilon _{ij}}$ ${\displaystyle {\boldsymbol {\varepsilon }}}$

${\displaystyle {\begin{aligned}\varepsilon _{ij}&={\frac {1}{2}}\left(u_{i,j}+u_{j,i}\right)\\&= \left[{\begin{matrice}\varepsilon _{11}&\varepsilon _{12}&\varepsilon _{13}\\\varepsilon _{21}&\varepsilon _{22}&\varepsilon _{23 }\\\varepsilon _{31}&\varepsilon _{32}&\varepsilon _{33}\\\end{matrice}}\right]\\&=\left[{\begin{matrix}{\frac {\partial u_{1}}{\partial x_{1}}}&{\frac {1}{2}}\gauche({\frac {\partial u_{1}}{\partial x_{2}} }+{\frac {\partial u_{2}}{\partial x_{1}}}\right)&{\frac {1}{2}}\left({\frac {\partial u_{1}} {\partial x_{3}}}+{\frac {\partial u_{3}}{\partial x_{1}}}\right)\\{\frac {1}{2}}\left({\ frac {\partial u_{2}}{\partial x_{1}}}+{\frac {\partial u_{1}}{\partial x_{2}}}\right)&{\frac {\partial u_ {2}}{\partial x_{2}}}&{\frac {1}{2}}\left({\frac {\partial u_{2}}{\partial x_{3}}}+{\ frac {\partial u_{3}}{\partial x_{2}}}\right)\\{\frac {1}{2}}\left({\frac {\partial u_{3}}{\partial x_{1}}}+{\frac {\partial u_{1}}{\partial x_{3}}}\right)&{\frac {1}{2}}\left({\frac {\partial u_{3}}{ \partial x_{2}}}+{\frac {\partial u_{2}}{\partial x_{3}}}\right)&{\frac {\partial u_{3}}{\partial x_{3 }}}\\\end{matrice}}\right]\end{aligned}}}$

ou en utilisant une notation différente :

${\displaystyle \left[{\begin{matrix}\varepsilon _{xx}&\varepsilon _{xy}&\varepsilon _{xz}\\\varepsilon _{yx}&\varepsilon _{yy}&\varepsilon _{yz}\\\varepsilon _{zx}&\varepsilon _{zy}&\varepsilon _{zz}\\\end{matrice}}\right]=\left[{\begin{matrix}{\frac {\partial u_{x}}{\partial x}}&{\frac {1}{2}}\gauche({\frac {\partial u_{x}}{\partial y}}+{\frac { \partial u_{y}}{\partial x}}\right)&{\frac {1}{2}}\left({\frac {\partial u_{x}}{\partial z}}+{\ frac {\partial u_{z}}{\partial x}}\right)\\{\frac {1}{2}}\left({\frac {\partial u_{y}}{\partial x}} +{\frac {\partial u_{x}}{\partial y}}\right)&{\frac {\partial u_{y}}{\partial y}}&{\frac {1}{2}} \left({\frac {\partial u_{y}}{\partial z}}+{\frac {\partial u_{z}}{\partial y}}\right)\\{\frac {1}{ 2}}\left({\frac {\partial u_{z}}{\partial x}}+{\frac {\partial u_{x}}{\partial z}}\right)&{\frac {1 }{2}}\left({\frac {\partial u_{z}}{\partial y}}+{\frac {\partial u_{y}}{\partial z}}\right)&{\frac {\partial u_{z}}{\partial z}}\\\end{matrice}}\right]}$

De plus, puisque le gradient de déformation peut être exprimé comme où est le tenseur d'identité du second ordre, nous avons ${\displaystyle {\boldsymbol {F}}={\boldsymbol {\nabla }}\mathbf {u} +{\boldsymbol {I}}}$${\displaystyle {\boldsymbol {I}}}$

${\displaystyle {\boldsymbol {\varepsilon }}={\frac {1}{2}}\left({\boldsymbol {F}}^{T}+{\boldsymbol {F}}\right)-{\ symbole gras {I}}}$

De plus, à partir de l' expression générale des tenseurs de déformation finie lagrangienne et eulérienne, nous avons

${\displaystyle {\begin{aligned}\mathbf {E} _{(m)}&={\frac {1}{2m}}(\mathbf {U} ^{2m}-{\boldsymbol {I}} )={\frac {1}{2m}}[({\boldsymbol {F}}^{T}{\boldsymbol {F}})^{m}-{\boldsymbol {I}}]\approx {\ frac {1}{2m}}[\{{\boldsymbol {\nabla }}\mathbf {u} +({\boldsymbol {\nabla }}\mathbf {u} )^{T}+{\boldsymbol {I }}\}^{m}-{\boldsymbol {I}}]\approx {\boldsymbol {\varepsilon }}\\\mathbf {e} _{(m)}&={\frac {1}{2m }}(\mathbf {V} ^{2m}-{\boldsymbol {I}})={\frac {1}{2m}}[({\boldsymbol {F}}{\boldsymbol {F}}^{ T})^{m}-{\boldsymbol {I}}]\approx {\boldsymbol {\varepsilon }}\end{aligned}}}$

Dérivation géométrique

Figure 1. Déformation géométrique bidimensionnelle d'un élément matériel infinitésimal.

Considérons une déformation bidimensionnelle d'un élément matériel rectangulaire infinitésimal de dimensions par (figure 1), qui après déformation, prend la forme d'un losange. A partir de la géométrie de la figure 1, on a ${\displaystyle dx}$${\displaystyle dy}$

${\displaystyle {\begin{aligned}{\overline {ab}}&={\sqrt {\left(dx+{\frac {\partial u_{x}}{\partial x}}dx\right)^{2 }+\left({\frac {\partial u_{y}}{\partial x}}dx\right)^{2}}}\\&=dx{\sqrt {1+2{\frac {\partial u_{x}}{\partial x}}+\left({\frac {\partial u_{x}}{\partial x}}\right)^{2}+\left({\frac {\partial u_ {y}}{\partial x}}\right)^{2}}}\\\end{aligned}}}$

Pour de très petits gradients de déplacement, c'est-à-dire , nous avons ${\displaystyle \|\nabla \mathbf {u} \|\ll 1}$

${\displaystyle {\overline {ab}}\approx dx+{\frac {\partial u_{x}}{\partial x}}dx}$

La déformation normale dans la direction de l'élément rectangulaire est définie par ${\style d'affichage x}$

${\displaystyle \varepsilon _{x}={\frac {{\overline {ab}}-{\overline {AB}}}{\overline {AB}}}}$

et sachant cela , nous avons ${\displaystyle {\overline {AB}}=dx}$

${\displaystyle \varepsilon _{x}={\frac {\partial u_{x}}{\partial x}}}$

De même, la déformation normale dans la direction -, et -direction, devient ${\style d'affichage y}$${\style d'affichage z}$

${\displaystyle \varepsilon _{y}={\frac {\partial u_{y}}{\partial y}}\quad ,\qquad \varepsilon _{z}={\frac {\partial u_{z}} {\partiel z}}}$

La déformation de cisaillement technique , ou le changement d'angle entre deux lignes de matériau à l'origine orthogonales, dans ce cas la ligne et , est définie comme ${\displaystyle {\overline {AC}}}$${\displaystyle {\overline {AB}}}$

${\displaystyle \gamma _{xy}=\alpha +\beta }$

A partir de la géométrie de la figure 1, on a

${\displaystyle \tan \alpha ={\frac {{\dfrac {\partial u_{y}}{\partial x}}dx}{dx+{\dfrac {\partial u_{x}}{\partial x}} dx}}={\frac {\dfrac {\partial u_{y}}{\partial x}}{1+{\dfrac {\partial u_{x}}{\partial x}}}}\quad ,\ qquad \tan \beta ={\frac {{\dfrac {\partial u_{x}}{\partial y}}dy}{dy+{\dfrac {\partial u_{y}}{\partial y}}dy} }={\frac {\dfrac {\partial u_{x}}{\partial y}}{1+{\dfrac {\partial u_{y}}{\partial y}}}}}$

Pour les petites rotations, c'est -à- dire et sommes nous avons ${\style d'affichage \alpha }$${\displaystyle \beta }$${\style d'affichage \ll 1}$

${\displaystyle \tan \alpha \approx \alpha \quad ,\qquad \tan \beta \approx \beta }$

et, encore une fois, pour les petits gradients de déplacement, nous avons

${\displaystyle \alpha ={\frac {\partial u_{y}}{\partial x}}\quad ,\qquad \beta ={\frac {\partial u_{x}}{\partial y}}}$

Donc

${\displaystyle \gamma _{xy}=\alpha +\beta ={\frac {\partial u_{y}}{\partial x}}+{\frac {\partial u_{x}}{\partial y} }}$

En interchangeant et et et , on peut montrer que${\style d'affichage x}$${\style d'affichage y}$${\style d'affichage u_{x}}$${\displaystyle u_{y}}$${\displaystyle \gamma _{xy}=\gamma _{yx}}$

De même, pour les plans - et - , on a ${\style d'affichage y}$${\style d'affichage z}$${\style d'affichage x}$${\style d'affichage z}$

${\displaystyle \gamma _{yz}=\gamma _{zy}={\frac {\partial u_{y}}{\partial z}}+{\frac {\partial u_{z}}{\partial y }}\quad ,\qquad \gamma _{zx}=\gamma _{xz}={\frac {\partial u_{z}}{\partial x}}+{\frac {\partial u_{x}} {\partiel z}}}$

On peut voir que les composants de déformation de cisaillement tensoriel du tenseur de déformation infinitésimal peuvent alors être exprimés en utilisant la définition de déformation d'ingénierie, , comme ${\style d'affichage \gamma }$

$${\displaystyle \left[{\begin{matrix}\varepsilon _{xx}&\varepsilon _{xy}&\varepsilon _{xz}\\\varepsilon _{yx}&\varepsilon _{yy}&\varepsilon _{yz}\\\varepsilon _{zx}&\varepsilon _{zy}&\varepsilon _{zz}\\\end{matrice}}\right]=\left[{\begin{matrice}\varepsilon _ {xx}&\gamma _{xy}/2&\gamma _{xz}/2\\\gamma _{yx}/2&\varepsilon _{yy}&\gamma _{yz}/2\\\gamma _ {zx}/2&\gamma _{zy}/2&\varepsilon _{zz}\\\end{matrice}}\right]}$$

Interprétation physique

De la théorie des déformations finies, nous avons

${\displaystyle d\mathbf {x} ^{2}-d\mathbf {X} ^{2}=d\mathbf {X} \cdot 2\mathbf {E} \cdot d\mathbf {X} \quad { \text{ou}}\quad (dx)^{2}-(dX)^{2}=2E_{KL}\,dX_{K}\,dX_{L}}$

Pour des déformations infinitésimales alors on a

${\displaystyle d\mathbf {x} ^{2}-d\mathbf {X} ^{2}=d\mathbf {X} \cdot 2\mathbf {\boldsymbol {\varepsilon }} \cdot d\mathbf { X} \quad {\text{ou}}\quad (dx)^{2}-(dX)^{2}=2\varepsilon _{KL}\,dX_{K}\,dX_{L}}$

En divisant par nous avons ${\style d'affichage (dX)^{2}}$

${\displaystyle {\frac {dx-dX}{dX}}{\frac {dx+dX}{dX}}=2\varepsilon _{ij}{\frac {dX_{i}}{dX}}{\ frac {dX_{j}}{dX}}}$

Pour les petites déformations on suppose que , donc le second terme du membre de gauche devient : . ${\displaystyle dx\environ dX}$${\displaystyle {\frac {dx+dX}{dX}}\environ 2}$

Ensuite nous avons

${\displaystyle {\frac {dx-dX}{dX}}=\varepsilon _{ij}N_{i}N_{j}=\mathbf {N} \cdot {\boldsymbol {\varepsilon }}\cdot \mathbf {N} }$

où , est le vecteur unitaire dans la direction de , et l'expression de gauche est la déformation normale dans la direction de . Pour le cas particulier de dans la direction, c'est -à- dire , on a ${\displaystyle N_{i}={\frac {dX_{i}}{dX}}}$${\displaystyle d\mathbf {X} }$ ${\displaystyle e_{(\mathbf {N} )}}$${\displaystyle \mathbf {N} }$${\displaystyle \mathbf {N} }$${\style d'affichage X_{1}}$${\displaystyle \mathbf {N} =\mathbf {I} _{1}}$

${\displaystyle e_{(\mathbf {I} _{1})}=\mathbf {I} _{1}\cdot {\boldsymbol {\varepsilon }}\cdot \mathbf {I} _{1}=\ varepsilon _{11}}$

De même, pour et nous pouvons trouver les déformations normales et , respectivement. Par conséquent, les éléments diagonaux du tenseur de déformation infinitésimal sont les déformations normales dans les directions des coordonnées. ${\displaystyle \mathbf {N} =\mathbf {I} _{2}}$${\displaystyle \mathbf {N} =\mathbf {I} _{3}}$${\displaystyle \varepsilon _{22}}$${\displaystyle \varepsilon _{33}}$

Règles de transformation de contrainte

Si nous choisissons un système de coordonnées orthonormé ( ), nous pouvons écrire le tenseur en termes de composantes par rapport à ces vecteurs de base comme ${\displaystyle \mathbf {e} _{1},\mathbf {e} _{2},\mathbf {e} _{3}}$

${\displaystyle {\boldsymbol {\varepsilon }}=\sum _{i=1}^{3}\sum _{j=1}^{3}\varepsilon _{ij}\mathbf {e} _{i }\otimes \mathbf {e} _{j}}$

Sous forme matricielle,

${\displaystyle {\underline {\underline {\boldsymbol {\varepsilon }}}}={\begin{bmatrix}\varepsilon _{11}&\varepsilon _{12}&\varepsilon _{13}\\\varepsilon _{12}&\varepsilon _{22}&\varepsilon _{23}\\\varepsilon _{13}&\varepsilon _{23}&\varepsilon _{33}\end{bmatrix}}}$

Nous pouvons facilement choisir d'utiliser un autre système de coordonnées orthonormé ( ) à la place. Dans ce cas, les composantes du tenseur sont différentes, disons ${\displaystyle {\hat {\mathbf {e} }}_{1},{\hat {\mathbf {e} }}_{2},{\hat {\mathbf {e} }}_{3} }$

${\displaystyle {\boldsymbol {\varepsilon }}=\sum _{i=1}^{3}\sum _{j=1}^{3}{\hat {\varepsilon }}_{ij}{\ chapeau {\mathbf {e} }}_{i}\otimes {\hat {\mathbf {e} }}_{j}\quad \implies \quad {\underline {\underline {\hat {\boldsymbol {\ varepsilon }}}}}={\begin{bmatrix}{\hat {\varepsilon }}_{11}&{\hat {\varepsilon }}_{12}&{\hat {\varepsilon }}_{13 }\\{\hat {\varepsilon }}_{12}&{\hat {\varepsilon }}_{22}&{\hat {\varepsilon }}_{23}\\{\hat {\varepsilon } }_{13}&{\hat {\varepsilon }}_{23}&{\hat {\varepsilon }}_{33}\end{bmatrix}}}$

Les composantes de la déformation dans les deux systèmes de coordonnées sont liées par

${\displaystyle {\hat {\varepsilon }}_{ij}=\ell _{ip}~\ell _{jq}~\varepsilon _{pq}}$

où la convention de sommation d'Einstein pour les indices répétés a été utilisée et . Sous forme matricielle ${\displaystyle \ell _{ij}={\hat {\mathbf {e} }}_{i}\cdot \mathbf {e} _{j}}$

${\displaystyle {\underline {\underline {\hat {\boldsymbol {\varepsilon }}}}}={\underline {\underline {\mathbf {L} }}}~{\underline {\underline {\boldsymbol { \varepsilon }}}}~{\underline {\underline {\mathbf {L} }}}^{T}}$

ou

${\displaystyle {\begin{bmatrix}{\hat {\varepsilon }}_{11}&{\hat {\varepsilon }}_{12}&{\hat {\varepsilon }}_{13}\\{ \hat {\varepsilon }}_{21}&{\hat {\varepsilon }}_{22}&{\hat {\varepsilon }}_{23}\\{\hat {\varepsilon }}_{31 }&{\hat {\varepsilon }}_{32}&{\hat {\varepsilon }}_{33}\end{bmatrix}}={\begin{bmatrix}\ell _{11}&\ell _ {12}&\ell _{13}\\\ell _{21}&\ell _{22}&\ell _{23}\\\ell _{31}&\ell _{32}&\ell _{33}\end{bmatrix}}{\begin{bmatrix}\varepsilon _{11}&\varepsilon _{12}&\varepsilon _{13}\\\varepsilon _{21}&\varepsilon _{22 }&\varepsilon _{23}\\\varepsilon _{31}&\varepsilon _{32}&\varepsilon _{33}\end{bmatrix}}{\begin{bmatrix}\ell _{11}&\ ell _{12}&\ell _{13}\\\ell _{21}&\ell _{22}&\ell _{23}\\\ell _{31}&\ell _{32}& \ell _{33}\end{bmatrix}}^{T}}$

Invariants de déformation

Certaines opérations sur le tenseur de déformation donnent le même résultat quel que soit le repère orthonormé utilisé pour représenter les composantes de déformation. Les résultats de ces opérations sont appelés invariants de déformation . Les invariants de déformation les plus couramment utilisés sont

${\displaystyle {\begin{aligned}I_{1}&=\mathrm {tr} ({\boldsymbol {\varepsilon }})\\I_{2}&={\tfrac {1}{2}}\{ [\mathrm {tr} ({\boldsymbol {\varepsilon }})]^{2}-\mathrm {tr} ({\boldsymbol {\varepsilon }}^{2})\}\\I_{3}& =\det({\boldsymbol {\varepsilon }})\end{aligned}}}$

En termes de composants

${\displaystyle {\begin{aligned}I_{1}&=\varepsilon _{11}+\varepsilon _{22}+\varepsilon _{33}\\I_{2}&=\varepsilon _{12}^ {2}+\varepsilon _{23}^{2}+\varepsilon _{31}^{2}-\varepsilon _{11}\varepsilon _{22}-\varepsilon _{22}\varepsilon _{33 }-\varepsilon _{33}\varepsilon _{11}\\I_{3}&=\varepsilon _{11}(\varepsilon _{22}\varepsilon _{33}-\varepsilon _{23}^{ 2})-\varepsilon _{12}(\varepsilon _{11}\varepsilon _{33}-\varepsilon _{23}\varepsilon _{31})+\varepsilon _{13}(\varepsilon _{21 }\varepsilon _{32}-\varepsilon _{22}\varepsilon _{31})\end{aligned}}}$

Principales souches

On peut montrer qu'il est possible de trouver un système de coordonnées ( ) dans lequel les composantes du tenseur de déformation sont ${\displaystyle \mathbf {n} _{1},\mathbf {n} _{2},\mathbf {n} _{3}}$

${\displaystyle {\underline {\underline {\boldsymbol {\varepsilon }}}}={\begin{bmatrix}\varepsilon _{1}&0&0\\0&\varepsilon _{2}&0\\0&0&\varepsilon _{ 3}\end{bmatrix}}\quad \implies \quad {\boldsymbol {\varepsilon }}=\varepsilon _{1}\mathbf {n} _{1}\otimes \mathbf {n} _{1}+ \varepsilon _{2}\mathbf {n} _{2}\otimes \mathbf {n} _{2}+\varepsilon _{3}\mathbf {n} _{3}\otimes \mathbf {n} _ {3}}$

Les composantes du tenseur de déformation dans le système de coordonnées ( ) sont appelées déformations principales et les directions sont appelées directions de déformation principale. Puisqu'il n'y a pas de composants de déformation de cisaillement dans ce système de coordonnées, les déformations principales représentent les étirements maximum et minimum d'un volume élémentaire. ${\displaystyle \mathbf {n} _{1},\mathbf {n} _{2},\mathbf {n} _{3}}$${\displaystyle \mathbf {n} _{i}}$

Si on nous donne les composantes du tenseur de déformation dans un repère orthonormé arbitraire, on peut trouver les déformations principales en utilisant une décomposition en valeurs propres déterminée en résolvant le système d'équations

${\displaystyle ({\underline {\underline {\boldsymbol {\varepsilon }}}}-\varepsilon _{i}~{\underline {\underline {\mathbf {I} }}})~\mathbf {n} _{i}={\underline {\mathbf {0} }}}$

Ce système d'équations équivaut à trouver le vecteur le long duquel le tenseur de déformation devient un étirement pur sans composante de cisaillement. ${\displaystyle \mathbf {n} _{i}}$

Déformation volumétrique

La dilatation (la variation relative du volume) est le premier invariant de déformation ou trace du tenseur :

${\displaystyle \delta ={\frac {\Delta V}{V_{0}}}=I_{1}=\varepsilon _{11}+\varepsilon _{22}+\varepsilon _{33}}$

En fait, si l'on considère un cube de longueur d'arête a , c'est un quasi-cube après la déformation (les variations des angles ne changent pas le volume) avec les dimensions et V ₀ = a ³ , donc ${\displaystyle a\cdot (1+\varepsilon _{11})\times a\cdot (1+\varepsilon _{22})\times a\cdot (1+\varepsilon _{33})}$

${\displaystyle {\frac {\Delta V}{V_{0}}}={\frac {\left(1+\varepsilon _{11}+\varepsilon _{22}+\varepsilon _{33}+\ varepsilon _{11}\cdot \varepsilon _{22}+\varepsilon _{11}\cdot \varepsilon _{33}+\varepsilon _{22}\cdot \varepsilon _{33}+\varepsilon _{11} \cdot \varepsilon _{22}\cdot \varepsilon _{33}\right)\cdot a^{3}-a^{3}}{a^{3}}}}$

quand on considère de petites déformations,

${\displaystyle 1\gg \varepsilon _{ii}\gg \varepsilon _{ii}\cdot \varepsilon _{jj}\gg \varepsilon _{11}\cdot \varepsilon _{22}\cdot \varepsilon _{ 33}}$

donc la formule.

Variation réelle de volume (en haut) et approchée (en bas) : le dessin vert montre le volume estimé et le dessin orange le volume négligé

En cas de cisaillement pur, on constate qu'il n'y a pas de changement de volume.

Tenseur de déviateur de déformation

Le tenseur de déformation infinitésimal , de la même manière que le tenseur de contrainte de Cauchy , peut être exprimé comme la somme de deux autres tenseurs : ${\displaystyle \varepsilon _{ij}}$

1. un tenseur de déformation moyenne ou tenseur de déformation volumétrique ou tenseur de déformation sphérique , liés à la dilatation ou de changement de volume; et${\displaystyle \varepsilon _{M}\delta _{ij}}$
2. une composante déviatorique appelée tenseur déviateur de déformation , , liée à la distorsion.${\displaystyle \varepsilon '_{ij}}$

${\displaystyle \varepsilon _{ij}=\varepsilon '_{ij}+\varepsilon _{M}\delta _{ij}}$

où est la déformation moyenne donnée par ${\displaystyle \varepsilon _{M}}$

${\displaystyle \varepsilon _{M}={\frac {\varepsilon _{kk}}{3}}={\frac {\varepsilon _{11}+\varepsilon _{22}+\varepsilon _{33} }{3}}={\tfrac {1}{3}}I_{1}^{e}}$

Le tenseur de déformation déviatorique peut être obtenu en soustrayant le tenseur de déformation moyen du tenseur de déformation infinitésimal :

${\displaystyle {\begin{aligned}\ \varepsilon '_{ij}&=\varepsilon _{ij}-{\frac {\varepsilon _{kk}}{3}}\delta _{ij}\\\ gauche[{\begin{matrice}\varepsilon '_{11}&\varepsilon '_{12}&\varepsilon '_{13}\\\varepsilon '_{21}&\varepsilon '_{22}&\ varepsilon '_{23}\\\varepsilon '_{31}&\varepsilon '_{32}&\varepsilon '_{33}\\\end{matrice}}\right]&=\left[{\begin {matrice}\varepsilon _{11}&\varepsilon _{12}&\varepsilon _{13}\\\varepsilon _{21}&\varepsilon _{22}&\varepsilon _{23}\\\varepsilon _ {31}&\varepsilon _{32}&\varepsilon _{33}\\\end{matrice}}\right]-\left[{\begin{matrice}\varepsilon _{M}&0&0\\0&\varepsilon _{M}&0\\0&0&\varepsilon _{M}\\\end{matrice}}\right]\\&=\left[{\begin{matrice}\varepsilon _{11}-\varepsilon _{M }&\varepsilon _{12}&\varepsilon _{13}\\\varepsilon _{21}&\varepsilon _{22}-\varepsilon _{M}&\varepsilon _{23}\\\varepsilon _{ 31}&\varepsilon _{32}&\varepsilon _{33}-\varepsilon _{M}\\\end{matrice}}\right]\\\end{aligned}}}$

Souches octaédriques

Soit ( ) les directions des trois déformations principales. Un plan octaédrique est un plan dont la normale fait des angles égaux avec les trois directions principales. La déformation de cisaillement d' ingénierie sur un plan octaédrique est appelée déformation de cisaillement octaédrique et est donnée par ${\displaystyle \mathbf {n} _{1},\mathbf {n} _{2},\mathbf {n} _{3}}$

${\displaystyle \gamma _{\mathrm {oct} }={\tfrac {2}{3}}{\sqrt {(\varepsilon _{1}-\varepsilon _{2})^{2}+(\ varepsilon _{2}-\varepsilon _{3})^{2}+(\varepsilon _{3}-\varepsilon _{1})^{2}}}}$

où sont les principales contraintes. ${\displaystyle \varepsilon _{1},\varepsilon _{2},\varepsilon _{3}}$

La déformation normale sur un plan octaédrique est donnée par

${\displaystyle \varepsilon _{\mathrm {oct} }={\tfrac {1}{3}}(\varepsilon _{1}+\varepsilon _{2}+\varepsilon _{3})}$

souche équivalente

Une quantité scalaire appelée déformation équivalente , ou déformation équivalente de von Mises , est souvent utilisée pour décrire l'état de déformation dans les solides. Plusieurs définitions de la contrainte équivalente peuvent être trouvées dans la littérature. Une définition couramment utilisée dans la littérature sur la plasticité est

${\displaystyle \varepsilon _{\mathrm {eq} }={\sqrt {{\tfrac {2}{3}}{\boldsymbol {\varepsilon }}^{\mathrm {dev} } :{\boldsymbol {\ varepsilon }}^{\mathrm {dev} }}}={\sqrt {{\tfrac {2}{3}}\varepsilon _{ij}^{\mathrm {dev} }\varepsilon _{ij}^{ \mathrm {dev} }}}~;~~{\boldsymbol {\varepsilon }}^{\mathrm {dev} }={\boldsymbol {\varepsilon }}-{\tfrac {1}{3}}\mathrm {tr} ({\boldsymbol {\varepsilon }})~{\boldsymbol {I}}}$

Cette quantité est le travail conjugué à la contrainte équivalente définie comme

${\displaystyle \sigma _{\mathrm {eq} }={\sqrt {{\tfrac {3}{2}}{\boldsymbol {\sigma }}^{\mathrm {dev} } :{\boldsymbol {\ sigma }}^{\mathrm {dev} }}}}$

Équations de compatibilité

Pour les composantes de déformation prescrites, l'équation du tenseur de déformation représente un système de six équations différentielles pour la détermination de trois composantes de déplacements , donnant un système surdéterminé. Ainsi, il n'existe généralement pas de solution pour un choix arbitraire de composants de déformation. Par conséquent, certaines restrictions, appelées équations de compatibilité , sont imposées aux composants de déformation. Avec l'ajout des trois équations de compatibilité, le nombre d'équations indépendantes est réduit à trois, correspondant au nombre de composants de déplacement inconnus. Ces contraintes sur le tenseur de déformation ont été découvertes par Saint-Venant , et sont appelées " équations de compatibilité de Saint Venant ". ${\displaystyle \varepsilon _{ij}}$${\displaystyle u_{i,j}+u_{j,i}=2\varepsilon _{ij}}$${\style d'affichage u_{i}}$

Les fonctions de compatibilité servent à assurer une fonction de déplacement continu à valeur unique . Si le milieu élastique est visualisé comme un ensemble de cubes infinitésimaux à l'état non contraint, une fois le milieu tendu, un tenseur de déformation arbitraire peut ne pas produire une situation dans laquelle les cubes déformés s'emboîtent toujours sans se chevaucher. ${\style d'affichage u_{i}}$

En notation index, les équations de compatibilité sont exprimées sous la forme

${\displaystyle \varepsilon _{ij,km}+\varepsilon _{km,ij}-\varepsilon _{ik,jm}-\varepsilon _{jm,ik}=0}$

Notation d'ingénierie

${\displaystyle {\frac {\partial ^{2}\epsilon _{x}}{\partial y^{2}}}+{\frac {\partial ^{2}\epsilon _{y}}{\ x partiel^{2}}}=2{\frac {\partial ^{2}\epsilon _{xy}}{\partial x\partial y}}}$ ${\displaystyle {\frac {\partial ^{2}\epsilon _{y}}{\partial z^{2}}}+{\frac {\partial ^{2}\epsilon _{z}}{\ partiel y^{2}}}=2{\frac {\partial ^{2}\epsilon _{yz}}{\partial y\partial z}}}$ ${\displaystyle {\frac {\partial ^{2}\epsilon _{x}}{\partial z^{2}}}+{\frac {\partial ^{2}\epsilon _{z}}{\ x partiel^{2}}}=2{\frac {\partial ^{2}\epsilon _{zx}}{\partial z\partial x}}}$ ${\displaystyle {\frac {\partial ^{2}\epsilon _{x}}{\partial y\partial z}}={\frac {\partial }{\partial x}}\left(-{\frac {\partial \epsilon _{yz}}{\partial x}}+{\frac {\partial \epsilon _{zx}}{\partial y}}+{\frac {\partial \epsilon _{xy}} {\partiel z}}\right)}$ ${\displaystyle {\frac {\partial ^{2}\epsilon _{y}}{\partial z\partial x}}={\frac {\partial }{\partial y}}\left({\frac { \partial \epsilon _{yz}}{\partial x}}-{\frac {\partial \epsilon _{zx}}{\partial y}}+{\frac {\partial \epsilon _{xy}}{ \partial z}}\right)}$ ${\displaystyle {\frac {\partial ^{2}\epsilon _{z}}{\partial x\partial y}}={\frac {\partial }{\partial z}}\left({\frac { \partial \epsilon _{yz}}{\partial x}}+{\frac {\partial \epsilon _{zx}}{\partial y}}-{\frac {\partial \epsilon _{xy}}{ \partial z}}\right)}$

Cas spéciaux

Contrainte plane

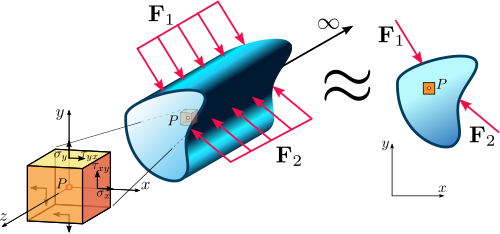
État de déformation plane dans un continu.

Dans les composants d'ingénierie réels, la contrainte (et la déformation) sont des tenseurs 3D, mais dans les structures prismatiques telles qu'une longue billette de métal, la longueur de la structure est beaucoup plus grande que les deux autres dimensions. Les déformations associées à la longueur, c'est-à-dire la déformation normale et les déformations de cisaillement et (si la longueur est la 3-direction) sont contraintes par le matériau voisin et sont petites par rapport aux déformations transversales . La déformation plane est alors une approximation acceptable. Le tenseur de déformation pour la déformation plane s'écrit : ${\displaystyle \varepsilon _{33}}$${\displaystyle \varepsilon _{13}}$${\displaystyle \varepsilon _{23}}$

${\displaystyle {\underline {\underline {\boldsymbol {\varepsilon }}}}={\begin{bmatrix}\varepsilon _{11}&\varepsilon _{12}&0\\\varepsilon _{21}&\ varepsilon _{22}&0\\0&0&0\end{bmatrice}}}$

dans laquelle le double soulignement indique un tenseur du second ordre . Cet état de déformation est appelé déformation plane . Le tenseur des contraintes correspondant est :

${\displaystyle {\underline {\underline {\boldsymbol {\sigma }}}}={\begin{bmatrix}\sigma _{11}&\sigma _{12}&0\\\sigma _{21}&\ sigma _{22}&0\\0&0&\sigma _{33}\end{bmatrice}}}$

dans lequel le non-zéro est nécessaire pour maintenir la contrainte . Ce terme de contrainte peut être temporairement supprimé de l'analyse pour ne laisser que les termes dans le plan, réduisant ainsi le problème 3-D à un problème 2-D beaucoup plus simple. ${\displaystyle \sigma _{33}}$${\displaystyle \epsilon _{33}=0}$

Contrainte anti-plan

La déformation antiplane est un autre état de déformation spécial qui peut se produire dans un corps, par exemple dans une région proche d'une luxation de vis . Le tenseur de déformation pour la déformation antiplane est donné par

${\displaystyle {\underline {\underline {\boldsymbol {\varepsilon }}}}={\begin{bmatrix}0&0&\varepsilon _{13}\\0&0&\varepsilon _{23}\\\varepsilon _{13} &\varepsilon _{23}&0\end{bmatrix}}}$

Tenseur de rotation infinitésimal

Le tenseur de déformation infinitésimal est défini comme

${\displaystyle {\boldsymbol {\varepsilon }}={\frac {1}{2}}[{\boldsymbol {\nabla }}\mathbf {u} +({\boldsymbol {\nabla }}\mathbf {u } )^{T}]}$

Par conséquent, le gradient de déplacement peut être exprimé comme

${\displaystyle {\boldsymbol {\nabla }}\mathbf {u} ={\boldsymbol {\varepsilon }}+{\boldsymbol {\omega }}}$

où

${\displaystyle {\boldsymbol {\omega }}:={\frac {1}{2}}[{\boldsymbol {\nabla }}\mathbf {u} -({\boldsymbol {\nabla }}\mathbf { u} )^{T}]}$

La quantité est le tenseur de rotation infinitésimal . Ce tenseur est antisymétrique . Pour les déformations infinitésimales, les composantes scalaires de satisfont à la condition . On notera que le gradient de déplacement est faible seulement si à la fois le tenseur de déformation et la rotation tenseur sont infinitésimal. ${\displaystyle {\boldsymbol {\omega }}}$${\displaystyle {\boldsymbol {\omega }}}$${\displaystyle |\omega _{ij}|\ll 1}$

Le vecteur axial

Un tenseur du second ordre symétrique asymétrique a trois composantes scalaires indépendantes. Ces trois composantes sont utilisées pour définir un vecteur axial , , comme suit ${\displaystyle \mathbf {w} }$

${\displaystyle \omega _{ij}=-\epsilon _{ijk}~w_{k}~;~~w_{i}=-{\tfrac {1}{2}}~\epsilon _{ijk}~ \omega _{jk}}$

où est le symbole de permutation . Sous forme matricielle ${\displaystyle \epsilon _{ijk}}$

${\displaystyle {\underline {\underline {\boldsymbol {\omega }}}}={\begin{bmatrix}0&-w_{3}&w_{2}\\w_{3}&0&-w_{1}\\ -w_{2}&w_{1}&0\end{bmatrix}}~;~~{\underline {\mathbf {w} }}={\begin{bmatrix}w_{1}\\w_{2}\\ w_{3}\end{bmatrice}}}$

Le vecteur axial est également appelé vecteur de rotation infinitésimal . Le vecteur rotation est lié au gradient de déplacement par la relation

${\displaystyle \mathbf {w} ={\tfrac {1}{2}}~{\boldsymbol {\nabla }}\times \mathbf {u} }$

En notation indexée

${\displaystyle w_{i}={\tfrac {1}{2}}~\epsilon _{ijk}~u_{k,j}}$

Si et alors le matériau subit une rotation approximative du corps rigide de grandeur autour du vecteur . ${\displaystyle \lVert {\boldsymbol {\omega }}\rVert \ll 1}$${\displaystyle {\boldsymbol {\varepsilon }}={\boldsymbol {0}}}$${\displaystyle |\mathbf {w} |}$${\displaystyle \mathbf {w} }$

Relation entre le tenseur de déformation et le vecteur rotation

Étant donné un champ de déplacement continu à valeur unique et le tenseur de déformation infinitésimal correspondant , nous avons (voir Dérivée du tenseur (mécanique des milieux continus ) ) ${\displaystyle \mathbf {u} }$${\displaystyle {\boldsymbol {\varepsilon }}}$

${\displaystyle {\boldsymbol {\nabla }}\times {\boldsymbol {\varepsilon }}=e_{ijk}~\varepsilon _{lj,i}~\mathbf {e} _{k}\otimes \mathbf { e} _{l}={\tfrac {1}{2}}~e_{ijk}~[u_{l,ji}+u_{j,li}]~\mathbf {e} _{k}\otimes \mathbf {e} _{l}}$

Puisqu'un changement dans l'ordre de différenciation ne change pas le résultat, . Par conséquent ${\style d'affichage u_{l,ji}=u_{l,ij}}$

${\displaystyle \,e_{ijk}u_{l,ji}=(e_{12k}+e_{21k})u_{l,12}+(e_{13k}+e_{31k})u_{l,13 }+(e_{23k}+e_{32k})u_{l,32}=0}$

Aussi

${\displaystyle {\tfrac {1}{2}}~e_{ijk}~u_{j,li}=\left({\tfrac {1}{2}}~e_{ijk}~u_{j,i }\right)_{,l}=\left({\tfrac {1}{2}}~e_{kij}~u_{j,i}\right)_{,l}=w_{k,l} }$

D'où

${\displaystyle {\boldsymbol {\nabla }}\times {\boldsymbol {\varepsilon }}=w_{k,l}~\mathbf {e} _{k}\otimes \mathbf {e} _{l}= {\boldsymbol {\nabla }}\mathbf {w} }$

Relation entre le tenseur de rotation et le vecteur de rotation

A partir d'une identité importante concernant la boucle d'un tenseur, nous savons que pour un champ de déplacement continu à valeur unique , ${\displaystyle \mathbf {u} }$

${\displaystyle {\boldsymbol {\nabla }}\times ({\boldsymbol {\nabla }}\mathbf {u} )={\boldsymbol {0}}.}$

Puisque nous avons ${\displaystyle {\boldsymbol {\nabla }}\mathbf {u} ={\boldsymbol {\varepsilon }}+{\boldsymbol {\omega }}}$${\displaystyle {\boldsymbol {\nabla }}\times {\boldsymbol {\omega }}=-{\boldsymbol {\nabla }}\times {\boldsymbol {\varepsilon }}=-{\boldsymbol {\nabla } }\mathbf {w} .}$

Tenseur de déformation en coordonnées cylindriques

En coordonnées polaires cylindriques ( ), le vecteur de déplacement peut s'écrire sous la forme ${\style d'affichage r,\theta ,z}$

${\displaystyle \mathbf {u} =u_{r}~\mathbf {e} _{r}+u_{\theta }~\mathbf {e} _{\theta }+u_{z}~\mathbf {e } _{z}}$

Les composantes du tenseur de déformation dans un système de coordonnées cylindriques sont données par : ${\displaystyle {\begin{aligned}\varepsilon _{rr}&={\cfrac {\partial u_{r}}{\partial r}}\\\varepsilon _{\theta \theta }&={\cfrac {1}{r}}\gauche({\cfrac {\partial u_{\theta }}{\partial \theta }}+u_{r}\right)\\\varepsilon _{zz}&={\cfrac {\partial u_{z}}{\partial z}}\\\varepsilon _{r\theta }&={\cfrac {1}{2}}\left({\cfrac {1}{r}}{ \cfrac {\partial u_{r}}{\partial \theta }}+{\cfrac {\partial u_{\theta }}{\partial r}}-{\cfrac {u_{\theta }}{r} }\right)\\\varepsilon _{\theta z}&={\cfrac {1}{2}}\left({\cfrac {\partial u_{\theta }}{\partial z}}+{\ cfrac {1}{r}}{\cfrac {\partial u_{z}}{\partial \theta }}\right)\\\varepsilon _{zr}&={\cfrac {1}{2}}\ gauche({\cfrac {\partial u_{r}}{\partial z}}+{\cfrac {\partial u_{z}}{\partial r}}\right)\end{aligned}}}$

Tenseur de déformation en coordonnées sphériques

En coordonnées sphériques ( ), le vecteur de déplacement peut s'écrire sous la forme ${\displaystyle r,\theta ,\phi }$

Les coordonnées sphériques ( r , θ , & phiv ) que celle couramment utilisée dans la physique : la distance radiale r , l' angle polaire thetav ( thêta ), et l' angle azimutal φ ( phi ). Le symbole ρ ( rho ) est souvent utilisé au lieu de r .

${\displaystyle \mathbf {u} =u_{r}~\mathbf {e} _{r}+u_{\theta }~\mathbf {e} _{\theta }+u_{\phi }~\mathbf { e} _{\phi }}$

Les composantes du tenseur de déformation dans un système de coordonnées sphériques sont données par

${\displaystyle {\begin{aligned}\varepsilon _{rr}&={\cfrac {\partial u_{r}}{\partial r}}\\\varepsilon _{\theta \theta }&={\cfrac {1}{r}}\gauche({\cfrac {\partial u_{\theta }}{\partial \theta }}+u_{r}\right)\\\varepsilon _{\phi \phi }&= {\cfrac {1}{r\sin \theta }}\left({\cfrac {\partial u_{\phi }}{\partial \phi }}+u_{r}\sin \theta +u_{\theta }\cos \theta \right)\\\varepsilon _{r\theta }&={\cfrac {1}{2}}\left({\cfrac {1}{r}}{\cfrac {\partial u_ {r}}{\partial \theta }}+{\cfrac {\partial u_{\theta }}{\partial r}}-{\cfrac {u_{\theta }}{r}}\right)\\ \varepsilon _{\theta \phi }&={\cfrac {1}{2r}}\left({\cfrac {1}{\sin \theta }}{\cfrac {\partial u_{\theta }}{ \partial \phi }}+{\cfrac {\partial u_{\phi }}{\partial \theta }}-u_{\phi }\cot \theta \right)\\\varepsilon _{\phi r}& ={\cfrac {1}{2}}\left({\cfrac {1}{r\sin \theta }}{\cfrac {\partial u_{r}}{\partial \phi }}+{\cfrac {\partial u_{\phi }}{\partial r}}-{\cfrac {u_{\phi }}{r}}\right)\end{aligned}}}$