Carré d'opposition - Square of opposition

* Carré d'opposition. * Les lettres minuscules (a, e, i, o) sont utilisées ici à la place des lettres majuscules (A, E, I, O) afin d'être visuellement distinguées des lettres majuscules environnantes S (Terme sujet) et P (terme prédicat). * Dans les diagrammes de Venn , les zones noires sont vides et les zones rouges ne sont pas vides. Les zones blanches peuvent être vides ou non. * Les flèches fanées et les zones rouges fanées s'appliquent dans la logique traditionnelle en supposant l'existence de choses déclarées comme S (ou de choses satisfaisant une déclaration S dans la logique moderne). Dans la logique moderne, cela n'est pas supposé, donc les fanés ne tiennent pas. (Il ne peut y avoir aucun élément dans les zones rouges fanées dans la logique moderne.)

Représentation du XVe siècle

En terme logique (une branche de la logique philosophique ), le carré d'opposition est un diagramme représentant les relations entre les quatre propositions catégoriques de base . L'origine du carré remonte à Aristote faisant la distinction entre deux oppositions : contradiction et contrariété . Cependant, Aristote n'a dessiné aucun schéma. Cela a été fait plusieurs siècles plus tard par Apulée et Boèce .

Sommaire

Dans la logique traditionnelle, une proposition ( latin : propositio ) est une affirmation parlée ( oratio enunciativa ), et non le sens d'une affirmation, comme dans la philosophie moderne du langage et de la logique. Une proposition catégorique est une proposition simple contenant deux termes, sujet (S) et prédicat (P), dans laquelle le prédicat est soit affirmé, soit nié du sujet.

Chaque proposition catégorique peut être réduite à l' une des quatre formes logiques , appelé A , E , I et O sur la base du latin un ff i RMO (I affirmer), pour les propositions affirmatives A et I , et n e g o (I nier), pour les propositions négatives E et O . Ceux-ci sont:

• La proposition 'A', l'universelle affirmative ( universalis affirmativa ), dont la forme en latin est 'omne S est P', traduite habituellement par 'chaque S est un P'.
• La proposition « E », le négatif universel ( universalis negativa ), forme latine « nullum S est P », généralement traduite par « aucun S n'est P ».
• La proposition 'je', l'affirmatif particulier ( particularis affirmativa ), latin 'quoddam S est P', généralement traduit par 'certains S sont P'.
• La proposition 'O', le particulier négatif ( particularis negativa ), latin 'quoddam S nōn est P', généralement traduit par 'certains S ne sont pas P'.

Sous forme de tableau :

Les quatre propositions aristotéliciennes

Nom	symbole	Latin	Anglais*	Mnémonique	Forme moderne
Universel affirmatif	UNE	Omne S est P.	Tout S est P. (S est toujours P.)	a ffirmo (j'affirme)	${\displaystyle \forall x(Sx\rightarrow Px)}$
Négatif universel	E	Nullum S est P.	Non S n'est P. (S n'est jamais P.)	n e go (je nie)	${\displaystyle \forall x(Sx\rightarrow \neg Px)}$
Particulier affirmatif	je	Quoddam S est P.	Certains S est P. (S est parfois P.)	aff i rmo (j'affirme)	${\displaystyle \exists x(Sx\land Px)}$
Négatif particulier	O	Quoddam S nōn est P.	Certains S n'est pas P. (S n'est pas toujours P.)	neg o (je nie)	${\displaystyle \exists x(Sx\land \neg Px)}$

* La proposition 'A' peut être énoncée comme "Tout S est P." Cependant, la proposition 'E' lorsqu'elle est énoncée de manière correspondante comme "Tout S n'est pas P." est ambigu car il peut s'agir d'une proposition E ou O, nécessitant ainsi un contexte pour déterminer la forme ; la forme standard "No S is P" est sans ambiguïté, elle est donc préférée. La proposition 'O' prend également la forme "Parfois S n'est pas P." et "Un certain S n'est pas P." (littéralement le latin 'Quoddam S nōn est P.')

** dans les formes modernes signifie qu'une déclaration s'applique sur un objet . Il peut être simplement interprété comme " est " dans de nombreux cas. peut aussi s'écrire . ${\displaystyle Sx}$${\style d'affichage S}$${\style d'affichage x}$${\style d'affichage x}$${\style d'affichage S}$${\displaystyle Sx}$${\style d'affichage S(x)}$

Aristote déclare (dans les chapitres six et sept des Peri hermēneias (Περὶ Ἑρμηνείας, Latin De Interpretatione , anglais 'On Interpretation')), qu'il existe certaines relations logiques entre ces quatre types de propositions. Il dit qu'à chaque affirmation correspond exactement une négation, et que chaque affirmation et sa négation sont « opposées » de telle sorte que toujours l'une d'elles doit être vraie et l'autre fausse. Une paire d'une déclaration affirmative et sa négation est, il appelle, une « contradiction » (en latin médiéval, contradictio ). Des exemples de contradictions sont « tout homme est blanc » et « tout homme n'est pas blanc » (également lu comme « certains hommes ne sont pas blancs »), « aucun homme n'est blanc » et « certains hommes sont blancs ».

Les relations ci-dessous, contraire, sous-contraire, sous-alternance et superalternance, sont fondées sur l'hypothèse logique traditionnelle selon laquelle les choses déclarées comme S (ou les choses satisfaisant une déclaration S dans la logique moderne) existent. Si cette hypothèse est supprimée, alors ces relations ne tiennent pas.

Les déclarations « contraires » (médiévaux : contrariae ) sont telles que les deux déclarations ne peuvent pas être vraies en même temps. Des exemples en sont l'affirmation universelle « chaque homme est blanc » et le négatif universel « aucun homme n'est blanc ». Ceux-ci ne peuvent pas être vrais en même temps. Cependant, ceux-ci ne sont pas contradictoires car les deux peuvent être faux. Par exemple, il est faux que tout homme soit blanc, puisque certains hommes ne sont pas blancs. Pourtant, il est également faux qu'aucun homme n'est blanc, puisqu'il y a des hommes blancs.

Puisque tout énoncé a le contraire contradictoire (sa négation), et puisqu'un contradictoire est vrai quand son contraire est faux, il s'ensuit que les contraires des contraires (que les médiévaux appelaient subcontraries , subcontrariae ) peuvent tous les deux être vrais, mais ils ne peuvent pas tous les deux être faux. Puisque les sous-contraires sont des négations d'énoncés universels, ils ont été appelés énoncés « particuliers » par les logiciens médiévaux.

Une autre relation logique impliquée par cela, bien que non mentionnée explicitement par Aristote, est « l'alternance » ( alternatio ), consistant en « subalternation » et « suralternance ». La sous-alternance est une relation entre l'énoncé particulier et l'énoncé universel de même qualité (affirmative ou négative) telle que le particulier est impliqué par l'universel, tandis que la suralternance est une relation entre eux telle que la fausseté de l'universel (équivalente à la négation de l'universel) est impliquée par la fausseté du particulier (équivalente à la négation du particulier). (La suralternance est la contraposée de la sous-alternance.) Dans ces relations, le particulier est le subalterne de l'universel, qui est le superalterne du particulier. Par exemple, si « tout homme est blanc » est vrai, son contraire « aucun homme n'est blanc » est faux. Par conséquent, le contradictoire « quelqu'un est blanc » est vrai. De même, l'universel « aucun homme n'est blanc » implique le particulier « tous les hommes ne sont pas blancs ».

En résumé:

• Les affirmations universelles sont contraires : « tout homme est juste » et « aucun homme n'est juste » ne peuvent être vrais ensemble, bien que l'un puisse être vrai et l'autre faux, et aussi les deux puissent être faux (si au moins un homme est juste, et à au moins un homme n'est pas juste).
• Les déclarations particulières sont des sous-contraires. « Certains hommes sont justes » et « certains hommes ne sont pas justes » ne peuvent pas être faux ensemble.
• L'énoncé particulier d'une qualité est le subalterne de l'énoncé universel de cette même qualité, qui est le superalterne de l'énoncé particulier parce que dans la sémantique aristotélicienne « tout A est B » implique « un certain A est B » et « aucun A n'est B » implique 'certain A n'est pas B'. Notez que les interprétations formelles modernes des phrases anglaises interprètent « chaque A est B » comme « pour tout x, une déclaration indiquant que x est A implique une déclaration indiquant que x est B », ce qui n'implique pas « un certain x est A ». C'est une question d'interprétation sémantique, cependant, et ne signifie pas, comme on le prétend parfois, que la logique aristotélicienne est « fausse ».
• L'universel affirmatif ( A ) et le particulier négatif ( O ) sont contradictoires. Si un certain A n'est pas B, alors tout A n'est pas B. Inversement, bien que ce ne soit pas le cas en sémantique moderne, on pensait que si tout A n'est pas B, un certain A n'est pas B. Cette interprétation a causé des difficultés (voir au dessous de). Alors que le grec d'Aristote ne représente pas le négatif particulier comme « un certain A n'est pas B », mais comme « tous les A ne sont pas B », quelqu'un dans son commentaire sur le Peri hermaneias , rend le négatif particulier comme « quoddam A nōn est B », littéralement « un certain A n'est pas un B », et dans tous les écrits médiévaux sur la logique, il est d'usage de représenter la proposition particulière de cette manière.

Ces relations sont devenues la base d'un diagramme provenant de Boèce et utilisé par les logiciens médiévaux pour classer les relations logiques. Les propositions sont placées aux quatre coins d'un carré, et les relations représentées par des lignes tracées entre elles, d'où le nom de « Carré d'opposition ». On peut donc faire les cas suivants :

1. Si A est vrai, alors E est faux, I est vrai, O est faux ;
2. Si E est vrai, alors A est faux, I est faux, O est vrai ;
3. Si I est vrai, alors E est faux, A et O sont indéterminés ;
4. Si O est vrai, alors A est faux, E et I sont indéterminés ;
5. Si A est faux, alors O est vrai, E et I sont indéterminés ;
6. Si E est faux, alors I est vrai, A et O sont indéterminés ;
7. Si I est faux, alors A est faux, E est vrai, O est vrai ;
8. Si O est faux, alors A est vrai, E est faux, I est vrai.

Pour les mémoriser, les médiévaux inventèrent la rime latine suivante :

A adfirmat, negat E, sed universaliter ambae ;

I firmat, negat O, sed particulariter ambae.

Il affirme que A et E ne sont ni tous les deux vrais ni tous les deux faux dans chacun des cas ci-dessus. Il en va de même pour I et O . Alors que les deux premiers sont des énoncés universels, le couple I / O renvoie à des énoncés particuliers.

Le Carré des Oppositions a été utilisé pour les inférences catégoriques décrites par le philosophe grec Aristote : conversion , obversion et contraposition . Chacun de ces trois types d'inférence catégorique a été appliqué aux quatre formes logiques boéthiennes : A , E , I et O .

Le problème de l'importance existentielle

Les sous-contraires (I et O), que les logiciens médiévaux représentaient sous la forme « quoddam A est B » (un certain A particulier est B) et « quoddam A non est B » (un certain A particulier n'est pas B) ne peuvent pas être tous les deux faux, puisque leur les déclarations universelles contradictoires (aucun A n'est B / chaque A est B) ne peuvent pas être vraies toutes les deux. Cela conduit à une difficulté identifiée pour la première fois par Pierre Abélard (1079 – 21 avril 1142). « Un certain A est B » semble impliquer « quelque chose est A », en d'autres termes, il existe quelque chose qui est A. Par exemple, « un certain homme est blanc » semble impliquer qu'au moins une chose qui existe est un homme, à savoir l'homme qui doit être blanc, si 'quelqu'un est blanc' est vrai. Mais, « un homme n'est pas blanc » implique également que quelque chose en tant qu'homme existe, à savoir l'homme qui n'est pas blanc, si l'affirmation « un homme n'est pas blanc » est vraie. Mais la logique aristotélicienne exige que l'une de ces affirmations (plus généralement « un certain A particulier est B » et « un certain A particulier n'est pas B ») soit nécessairement vraie, c'est-à-dire que les deux ne peuvent pas être fausses. Par conséquent, puisque les deux déclarations impliquent la présence d'au moins une chose qui est un homme, la présence d'un homme ou d'hommes est suivie. Mais, comme Abélard le souligne dans la Dialectique, les hommes n'existeraient-ils sûrement pas ?

Car avec absolument aucun homme existant, ni la proposition « tout homme est un homme » n'est vraie ni « un homme n'est pas un homme ».

Abélard fait également remarquer que les sous-contraires contenant des termes sujets ne dénotant rien, comme « un homme qui est une pierre », sont tous deux faux.

Si « chaque homme-pierre est une pierre » est vrai, sa conversion per accidens est également vraie (« certaines pierres sont des hommes-pierre »). Mais aucune pierre n'est un homme-pierre, parce que ni cet homme ni cet homme etc. ne sont une pierre. Mais aussi ce « un certain homme-pierre n'est pas une pierre » est faux par nécessité, puisqu'il est impossible de supposer qu'il est vrai.

Terence Parsons (né en 1939) soutient que les philosophes anciens n'ont pas connu le problème de la portée existentielle car seules les formes A (affirmative universelle) et I (affirmative particulière) avaient une portée existentielle. (Si une déclaration comprend un terme tel que la déclaration est fausse si le terme n'a pas d'instances, c'est-à-dire qu'aucune chose associée au terme n'existe, alors la déclaration est dite avoir une importance existentielle par rapport à ce terme.)

Les affirmatifs ont une portée existentielle, et les négatifs n'en ont pas. Les anciens ne voyaient donc pas l'incohérence du carré telle que formulée par Aristote car il n'y avait pas d'incohérence à voir.

Il poursuit en citant un philosophe médiéval Guillaume de Moerbeke (1215-1235 - c. 1286),

Dans les propositions affirmatives, un terme est toujours affirmé pour supposer quelque chose. Ainsi, s'il suppose pour rien la proposition est fausse. Cependant, dans les propositions négatives, l'assertion est soit que le terme ne suppose pas quelque chose, soit qu'il suppose quelque chose dont le prédicat est vraiment nié. Ainsi une proposition négative a deux causes de vérité.

Et pointe vers la traduction de Boèce du travail d'Aristote comme donnant lieu à la notion erronée que la forme O a une portée existentielle.

Mais lorsque Boèce (477 - 524 après JC) commente ce texte, il illustre la doctrine d'Aristote avec le diagramme désormais célèbre, et il utilise la formulation « Certains hommes ne sont pas justes ». Cela doit donc lui avoir semblé être un équivalent naturel en latin. Cela nous semble étrange en anglais, mais cela ne l'a pas dérangé.

Carrés modernes d'opposition

Carré d'opposition de Frege
Le conträr ci-dessous est un erratum :
Il doit se lire subcontrarär

Au 19ème siècle, George Boole (novembre 1815 - 8 décembre 1864) a plaidé pour exiger l'importance existentielle sur les deux termes dans les revendications particulières (I et O), mais permettant à tous les termes des revendications universelles (A et E) de manquer d'importance existentielle. Cette décision a rendu les diagrammes de Venn particulièrement faciles à utiliser pour la logique des termes. Le carré d'opposition, sous cet ensemble booléen d'hypothèses, est souvent appelé le carré d'opposition moderne . Dans le carré moderne de l'opposition, les affirmations A et O sont contradictoires, tout comme E et I, mais toutes les autres formes d'opposition cessent de tenir ; il n'y a pas de contraires, de sous-contraires, de sous-alternances et de superalternances. Ainsi, d'un point de vue moderne, il est souvent logique de parler de « l' » opposition d'une affirmation, plutôt que d'insister, comme le faisaient les anciens logiciens, sur le fait qu'une affirmation a plusieurs opposés différents, qui sont en différents types d'opposition avec le Réclamer.

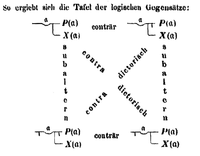
Le Begriffsschrift de Gottlob Frege (8 novembre 1848 - 26 juillet 1925) présente également un carré d'oppositions, organisé de manière presque identique au carré classique, montrant les contradictoires, subalternes et contraires entre quatre formules construites à partir de la quantification universelle, de la négation et de l'implication .

Le carré sémiotique d' Algirdas Julien Greimas (9 mars 1917 - 27 février 1992) est issu des travaux d'Aristote.

Le carré traditionnel de l'opposition est maintenant souvent comparé à des carrés basés sur la négation intérieure et extérieure.

Hexagones logiques et autres bi-simplexes

Le carré d'opposition a été étendu à un hexagone logique qui comprend les relations de six énoncés. Il a été découvert indépendamment par Augustin Sesmat (7 avril 1885 - 12 décembre 1957) et Robert Blanché (1898-1975). Il a été prouvé que le carré et l'hexagone, suivis d'un " cube logique ", appartiennent à une série régulière d'objets à n dimensions appelés " bi-simplexes logiques de dimension n ". Le modèle va même au-delà de cela.

Carré d'opposition (ou carré logique) et logique modale

Le carré logique, aussi appelé carré d'opposition ou carré d' Apulée a son origine dans les quatre phrases marquées à employer dans le raisonnement syllogistique : Tout homme est mauvais, l'universel affirmatif / et sa négation Pas tout homme est mauvais (ou Certains hommes sont pas mal), le particulier négatif d'une part / Certains hommes sont mauvais, le particulier affirmatif / et sa négation Aucun homme n'est mauvais, le négatif universel d'autre part. Robert Blanché a publié avec Vrin ses Structures intellectuelles en 1966 et depuis lors de nombreux savants pensent que le carré logique ou carré d'opposition représentant quatre valeurs devrait être remplacé par l' hexagone logique qui en représentant six valeurs est une figure plus puissante car elle a le pouvoir de expliquer plus de choses sur la logique et le langage naturel.

Interprétation ensembliste d'énoncés catégoriques

Dans la logique mathématique moderne , les énoncés contenant les mots « tous », « certains » et « non » peuvent être énoncés en termes de théorie des ensembles . Si l'ensemble de tous les A est étiqueté comme et l'ensemble de tous les B comme , alors : ${\style d'affichage s(A)}$${\style d'affichage s(B)}$

• « Tout A est B » (AaB) équivaut à « est un sous - ensemble de », ou .${\style d'affichage s(A)}$${\style d'affichage s(B)}$${\style d'affichage s(A)\subseteq s(B)}$
• "Aucun A n'est B" (AeB) équivaut à "L' intersection de et est vide ", ou .${\style d'affichage s(A)}$${\style d'affichage s(B)}$${\displaystyle s(A)\cap s(B)=\emptyset }$
• "Un certain A est B" (AiB) est équivalent à "L'intersection de et n'est pas vide", ou .${\style d'affichage s(A)}$${\style d'affichage s(B)}$${\displaystyle s(A)\cap s(B)\neq \emptyset }$
• « Certains A n'est pas B » (AoB) équivaut à « n'est pas un sous-ensemble de », ou .${\style d'affichage s(A)}$${\style d'affichage s(B)}$${\style d'affichage s(A)\nsous-ensemble s(B)}$

Par définition, l' ensemble vide est un sous-ensemble de tous les ensembles. De ce fait, il s'ensuit que, selon cette convention mathématique, s'il n'y a pas de A, alors les affirmations "Tout A est B" et "Aucun A n'est B" sont toujours vraies alors que les affirmations "Un certain A est B" et "Certains A n'est pas B" sont toujours faux. Cela implique également que AaB n'implique pas AiB, et certains des syllogismes mentionnés ci-dessus ne sont pas valides lorsqu'il n'y a pas de A ( ). ${\displaystyle \emptyset }$${\displaystyle s(A)=\emptyset }$

Voir également

• syllogistique de Boole
• Logique libre

Les références

Liens externes

• Parsons, Terence. "La Place Traditionnelle d'Opposition" . Dans Zalta, Edward N. (éd.). Encyclopédie de philosophie de Stanford .
• Congrès international sur la place de l'opposition
• Numéro spécial de Logica Universalis Vol. 2 N. 1 (2008) sur la Place de l'Opposition
• Catlogic : Un script informatique open source écrit en Ruby pour construire, étudier et calculer des propositions catégoriques et des syllogismes