Emission d'électrons de champ - Field electron emission
L'émission d'électrons de champ , également connue sous le nom d' émission de champ ( FE ) et d'émission de champ d'électrons , est une émission d' électrons induite par un champ électrostatique . Le contexte le plus courant est l'émission de champ d'une surface solide dans le vide . Cependant, l'émission de champ peut avoir lieu à partir de surfaces solides ou liquides , dans le vide, un fluide (par exemple l' air ), ou tout diélectrique non conducteur ou faiblement conducteur . La promotion induite par le champ des électrons de la bande de valence à la bande de conduction des semi - conducteurs (l' effet Zener ) peut également être considérée comme une forme d'émission de champ. La terminologie est historique car des phénomènes liés de photoeffet de surface, d' émission thermoionique (ou effet Richardson-Dushman ) et d'« émission électronique froide », c'est-à-dire l'émission d'électrons dans des champs électriques statiques (ou quasi-statiques) forts, ont été découverts et étudiés indépendamment de les années 1880 à 1930. Lorsque l'émission de champ est utilisée sans qualificatif, cela signifie généralement "émission froide".
L'émission de champ dans les métaux purs se produit dans des champs électriques élevés : les gradients sont généralement supérieurs à 1 gigavolt par mètre et dépendent fortement du travail de sortie . Alors que les sources d'électrons basées sur l'émission de champ ont un certain nombre d'applications, l'émission de champ est le plus souvent une source primaire indésirable de phénomènes de claquage du vide et de décharge électrique , que les ingénieurs s'efforcent d'empêcher. Des exemples d'applications pour l'émission de champ de surface comprennent la construction de sources d'électrons brillants pour les microscopes électroniques à haute résolution ou la décharge de charges induites par les engins spatiaux . Les dispositifs qui éliminent les charges induites sont appelés neutraliseurs de charges .
L'émission de champ a été expliquée par l'effet tunnel quantique des électrons à la fin des années 1920. Ce fut l'un des triomphes de la mécanique quantique naissante . La théorie de l'émission de champ des métaux en vrac a été proposée par Ralph H. Fowler et Lothar Wolfgang Nordheim . Une famille d'équations approchées, les équations de Fowler-Nordheim , porte leur nom. Strictement, les équations de Fowler-Nordheim s'appliquent uniquement à l'émission de champ des métaux en vrac et (avec une modification appropriée) à d'autres solides cristallins en vrac , mais elles sont souvent utilisées - comme une approximation grossière - pour décrire l'émission de champ d'autres matériaux.
Terminologie et conventions
Champ émission d'électrons , émission d'électrons induite par champ , émission de champ et émission de champ électronique sont des noms généraux de ce phénomène expérimental et sa théorie. Le prénom est utilisé ici.
L'effet tunnel de Fowler-Nordheim est l'effet tunnel mécanique des ondes d'électrons à travers une barrière triangulaire arrondie créée à la surface d'un conducteur d'électrons en appliquant un champ électrique très élevé. Des électrons individuels peuvent s'échapper par effet tunnel de Fowler-Nordheim à partir de nombreux matériaux dans diverses circonstances différentes.
L'émission d'électrons en champ froid (CFE) est le nom donné à un régime d'émission statistique particulier, dans lequel les électrons de l'émetteur sont initialement en équilibre thermodynamique interne, et dans lequel la plupart des électrons émis s'échappent par effet tunnel de Fowler-Nordheim à partir d'états électroniques proches du émetteur niveau de Fermi . (En revanche, dans lerégime d' émission de Schottky , la plupart des électrons s'échappent au-dessus d'une barrière à champ réduit, à partir d'états bien au-dessus du niveau de Fermi.) De nombreux matériaux solides et liquides peuvent émettre des électrons dans un régime CFE si un champ électrique d'un la taille appropriée est appliquée.
Les équations de type Fowler-Nordheim sont une famille d'équations approximatives dérivées pour décrire la CFE à partir des états électroniques internes dans les métaux en vrac. Les différents membres de la famille représentent différents degrés d'approximation à la réalité. Des équations approximatives sont nécessaires car, pour des modèles physiquement réalistes de la barrière tunnel, il est mathématiquement impossible en principe de résoudreexactement l' équation de Schrödinger d'une manière simple. Il n'y a aucune raison théorique de croire que les équations de type Fowler-Nordheim décrivent valablement l'émission de champ à partir de matériaux autres que les solides cristallins en vrac.
Pour les métaux, le régime CFE s'étend bien au-dessus de la température ambiante. Il existe d'autres régimes d'émission d'électrons (comme « l'émission thermique d'électrons » et « l' émission de Schottky ») qui nécessitent un échauffement externe important de l'émetteur. Il existe également des régimes d'émission où les électrons internes ne sont pas en équilibre thermodynamique et le courant d'émission est, en partie ou complètement, déterminé par l'apport d'électrons à la région émettrice. Un processus d'émission hors équilibre de ce type peut être appelé émission de champ (électron) si la plupart des électrons s'échappent par effet tunnel, mais il ne s'agit strictement pas d'un CFE et n'est pas décrit avec précision par une équation de type Fowler-Nordheim.
Des précautions sont nécessaires car dans certains contextes (par exemple, l'ingénierie des engins spatiaux), le nom « émission de champ » est appliqué à l'émission induite par le champ d'ions (émission d'ions de champ), plutôt que d'électrons, et parce que dans certains contextes théoriques, « l'émission de champ » est utilisé comme nom général couvrant à la fois l'émission d'électrons de champ et l'émission d'ions de champ.
Historiquement, le phénomène d'émission d'électrons de champ a été connu sous une variété de noms, y compris "l'effet aeona", "l'émission autoélectronique", "l'émission froide", "l'émission à cathode froide", "l'émission de champ", "l'émission d'électrons de champ". et "émission de champ d'électrons".
Les équations de cet article sont écrites à l'aide du Système international des quantités (ISQ). Il s'agit du système international moderne (après les années 1970), basé sur le système d'équations rationalisé mètre-kilogramme-seconde (rmks), qui est utilisé pour définir les unités SI. Littérature plus d'émissions sur le terrain (et des documents qui copient directement les équations de la littérature ancienne) écrivent souvent des équations en utilisant un système d'équations plus qui n'utilise pas la quantité ε 0 . Dans cet article, toutes ces équations ont été converties en forme internationale moderne. Pour plus de clarté, cela devrait toujours être fait.
Étant donné que la fonction de travail est normalement donnée en électronvolts (eV) et qu'il est souvent pratique de mesurer les champs en volts par nanomètre (V/nm), les valeurs de la plupart des constantes universelles sont données ici en unités impliquant les eV, V et nm. De plus en plus, c'est une pratique normale dans la recherche sur les émissions sur le terrain. Cependant, toutes les équations ici sont des équations compatibles ISQ et restent dimensionnellement cohérentes, comme l'exige le système international moderne. Pour indiquer leur statut, les valeurs numériques des constantes universelles sont attribuées à sept chiffres significatifs. Les valeurs sont dérivées des valeurs de 2006 des constantes fondamentales.
Début de l'histoire de l'émission d'électrons de champ
L'émission d'électrons de champ a une histoire longue, compliquée et désordonnée. Cette section couvre les débuts de l'histoire, jusqu'à la dérivation de l'équation originale de type Fowler-Nordheim en 1928.
Rétrospectivement, il semble probable que les décharges électriques rapportées par JH Winkler en 1744 aient été déclenchées par CFE à partir de son fil-électrode. Cependant, des recherches significatives ont dû attendre après l' identification de l'électron par JJ Thomson en 1897, et jusqu'à ce qu'il ait été compris - à partir des travaux d' émission thermique et de photo-émission - que les électrons pouvaient être émis à l'intérieur des métaux (plutôt qu'à partir de la surface). molécules de gaz adsorbées ), et que – en l'absence de champs appliqués – les électrons s'échappant des métaux devaient franchir une barrière de travail de sortie.
On soupçonnait au moins dès 1913 que l'émission induite par le champ était un effet physique distinct. Cependant, ce n'est qu'après que les techniques de nettoyage sous vide et de nettoyage des échantillons se sont considérablement améliorées que cela s'est bien établi. Lilienfeld (qui s'intéressait principalement aux sources d'électrons pour les applications médicales des rayons X ) publia en 1922 le premier compte rendu clair en anglais de la phénoménologie expérimentale de l'effet qu'il avait appelé « émission autoélectronique ». Il avait travaillé sur ce sujet, à Leipzig, depuis environ 1910. Kleint décrit ce travail et d'autres premiers.
Après 1922, l'intérêt expérimental s'est accru, notamment dans les groupes dirigés par Millikan au California Institute of Technology (Caltech) à Pasadena, Californie , et par Gossling à la General Electric Company à Londres. Les tentatives pour comprendre l'émission autoélectronique comprenaient le tracé de données expérimentales courant-tension ( i-V ) de différentes manières, pour rechercher une relation linéaire. Le courant augmentait avec la tension plus rapidement que linéairement, mais les tracés de type log( i ) en fonction de V n'étaient pas rectilignes. Walter H. Schottky a suggéré en 1923 que l'effet pourrait être dû à une émission induite thermiquement sur une barrière à champ réduit. Si c'est le cas, alors les tracés de log( i ) en fonction de √ V devraient être droits, mais ils ne l'étaient pas. L'explication de Schottky n'est pas non plus compatible avec l'observation expérimentale d'une très faible dépendance à la température dans le CFE – un point initialement négligé.
Une percée s'est produite lorsque CC Lauritsen (et J. Robert Oppenheimer indépendamment) a découvert que les tracés de log( i ) en fonction de 1/ V donnaient de bonnes lignes droites. Ce résultat, publié par Millikan et Lauritsen au début de 1928, était connu de Fowler et Nordheim .
Oppenheimer avait prédit que l'effet tunnel induit par le champ des électrons des atomes (l'effet maintenant appelé ionisation de champ) aurait cette dépendance i ( V ), avait trouvé cette dépendance dans les résultats expérimentaux publiés d'émission de champ de Millikan et Eyring, et a proposé que CFE était due à l' effet tunnel induit par le champ d'électrons provenant d'orbitales de type atomique dans les atomes métalliques de surface. Une théorie alternative de Fowler-Nordheim expliquait à la fois la découverte de Millikan-Lauritsen et la très faible dépendance du courant à la température. La théorie de Fowler-Nordheim a prédit que les deux seraient des conséquences si la CFE était due à un effet tunnel induit par le champ à partir d' états de type électron libre dans ce que nous appellerions maintenant une bande de conduction métallique , les états électroniques étant occupés conformément aux statistiques de Fermi-Dirac .
Oppenheimer avait des détails mathématiques de sa théorie sérieusement incorrects. Il y avait aussi une petite erreur numérique dans l'équation finale donnée par la théorie de Fowler-Nordheim pour la densité de courant CFE : cela a été corrigé dans l'article de 1929 de ( Stern, Gossling & Fowler 1929 ).
Strictement, si le champ barrière dans la théorie de Fowler-Nordheim 1928 est exactement proportionnel à la tension appliquée, et si la zone d'émission est indépendante de la tension, alors la théorie de Fowler-Nordheim 1928 prédit que les tracés de la forme (log( i / V 2 ) vs. 1/ V ) doivent être des droites exactes. Cependant, les techniques expérimentales contemporaines n'étaient pas assez bonnes pour faire la distinction entre le résultat théorique de Fowler-Nordheim et le résultat expérimental de Millikan-Lauritsen.
Ainsi, en 1928, une compréhension physique de base de l'origine du CFE à partir de métaux en vrac avait été obtenue et l'équation originale de type Fowler-Nordheim avait été dérivée.
La littérature présente souvent les travaux de Fowler-Nordheim comme une preuve de l'existence de l'effet tunnel électronique , comme prédit par la mécanique ondulatoire. Bien que cela soit correct, la validité de la mécanique ondulatoire a été largement acceptée en 1928. Le rôle le plus important de l'article de Fowler-Nordheim était qu'il s'agissait d'un argument convaincant de l'expérience que les statistiques de Fermi-Dirac s'appliquaient au comportement des électrons dans les métaux, comme suggéré par Sommerfeld en 1927. Le succès de la théorie de Fowler-Nordheim a fait beaucoup pour soutenir l'exactitude des idées de Sommerfeld et a grandement aidé à établir la théorie moderne des bandes d'électrons . En particulier, l'équation originale de type Fowler-Nordheim a été l'une des premières à incorporer les conséquences statistiques et mécaniques de l'existence du spin électronique dans la théorie d'un effet expérimental de matière condensée. L'article de Fowler-Nordheim a également établi la base physique d'un traitement unifié de l' émission d'électrons induite par champ et induite thermiquement . Avant 1928, on avait émis l'hypothèse que deux types d'électrons, les « thermions » et les « électrons de conduction », existaient dans les métaux, et que les courants d'électrons émis thermiquement étaient dus à l'émission de thermions, mais que les courants émis par le champ étaient dus à la émission d'électrons de conduction. Les travaux de Fowler-Nordheim 1928 ont suggéré que les thermions n'avaient pas besoin d'exister en tant que classe distincte d'électrons internes : les électrons pourraient provenir d'une seule bande occupée conformément aux statistiques de Fermi-Dirac, mais seraient émis de manière statistiquement différente dans différentes conditions de température et champ appliqué.
Les idées d' Oppenheimer , Fowler et Nordheim ont également été un stimulus important pour le développement, par George Gamow , et Ronald W. Gurney et Edward Condon , plus tard en 1928, de la théorie de la désintégration radioactive des noyaux (par effet tunnel de particules alpha ).
Applications pratiques : passé et présent
Comme déjà indiqué, les premiers travaux expérimentaux sur l'émission d'électrons de champ (1910-1920) ont été motivés par le désir de Lilienfeld de développer des tubes à rayons X miniaturisés pour des applications médicales. Cependant, il était trop tôt pour que cette technologie réussisse.
Après les travaux théoriques de Fowler-Nordheim en 1928, une avancée majeure est venue avec le développement en 1937 par Erwin W. Mueller du microscope électronique à champ (FEM) à géométrie sphérique (également appelé "microscope à émission de champ"). Dans cet instrument, l'émetteur d'électrons est un fil pointu, de rayon au sommet r . Celui-ci est placé, dans une enceinte sous vide, en face d'un détecteur d'images (à l'origine un écran phosphorescent), à une distance R de celui-ci. L'écran du microscope montre une image de projection de la distribution de la densité de courant J à travers le sommet de l'émetteur, avec un grossissement d'environ ( R / r ), typiquement 10 5 à 10 6 . Dans les études FEM, le rayon au sommet est généralement de 100 nm à 1 m. La pointe du fil pointu, lorsqu'elle est désignée comme un objet physique, a été appelée un « émetteur de champ », une « pointe » ou (récemment) un « émetteur Mueller ».
Lorsque la surface de l'émetteur est propre, cette image FEM est caractéristique de : (a) le matériau à partir duquel l'émetteur est fabriqué : (b) l'orientation du matériau par rapport à l'axe aiguille/fil ; et (c) dans une certaine mesure, la forme de la forme terminale de l'émetteur. Dans l'image FEM, les zones sombres correspondent à des régions où le travail de sortie local est relativement élevé et/ou le champ barrière local F est relativement faible, donc J est relativement faible ; les zones claires correspondent à des régions où φ est relativement faible et / ou F est relativement élevée, de sorte que J est relativement élevé. Ceci est tel que prédit par l'exposant des équations de type Fowler-Nordheim [voir éq. (30) ci-dessous].
L' adsorption de couches d'atomes de gaz (comme l'oxygène) sur la surface de l'émetteur, ou une partie de celle-ci, peut créer des dipôles électriques de surface qui modifient le travail de sortie local de cette partie de la surface. Cela affecte l'image FEM ; en outre, le changement de fonction de travail peut être mesuré à l'aide d'un tracé de Fowler-Nordheim (voir ci-dessous). Ainsi, le FEM est devenu un outil d'observation précoce de la science des surfaces . Par exemple, dans les années 1960, les résultats FEM ont contribué de manière significative aux discussions sur la catalyse hétérogène . FEM a également été utilisé pour des études de diffusion d'atomes de surface . Cependant, la FEM a maintenant été presque complètement remplacée par les nouvelles techniques de science des surfaces.
Une conséquence du développement FEM, et de l'expérimentation ultérieure, était qu'il est devenu possible d'identifier (à partir de l'inspection d'image FEM) quand un émetteur était « propre », et donc exhibant sa fonction de travail de surface propre telle qu'établie par d'autres techniques. Ceci était important dans les expériences conçues pour tester la validité de l'équation standard de type Fowler-Nordheim. Ces expériences ont déduit une valeur de tension à barrière de champ facteur de conversion β à partir d' un tracé Fowler-Nordheim (voir ci - dessous), en supposant que la surface propre φ -valeur de tungstène, et on les compare ceci avec des valeurs dérivées à partir de microscope électronique observations de forme de l'émetteur et modélisation électrostatique. Un accord à environ 10 % près a été obtenu. Ce n'est que très récemment qu'il a été possible de faire la comparaison dans l'autre sens, en amenant une sonde bien préparée si près d'une surface bien préparée qu'une géométrie approximative de plaques parallèles peut être supposée et que le facteur de conversion peut être considéré comme 1/ W , où W est la séparation sonde-émetteur mesurée. L'analyse du tracé de Fowler-Nordheim résultant donne une valeur de travail de sortie proche de la fonction de travail connue indépendamment de l'émetteur.
Spectroscopie électronique de champ (analyse d'énergie électronique)
Les mesures de distribution d'énergie des électrons émis par le champ ont été rapportées pour la première fois en 1939. En 1959, il a été réalisé théoriquement par Young et confirmé expérimentalement par Young et Mueller que la quantité mesurée en géométrie sphérique était la distribution de l'énergie totale de l'électron émis (son « répartition totale de l'énergie »). En effet, en géométrie sphérique, les électrons se déplacent de telle manière que le moment angulaire autour d'un point de l'émetteur est presque conservé. Par conséquent, toute énergie cinétique qui, à l'émission, est dans une direction parallèle à la surface de l'émetteur est convertie en énergie associée à la direction radiale du mouvement. Donc, ce qui est mesuré dans un analyseur d'énergie est l' énergie totale à l'émission.
Avec le développement d'analyseurs d'énergie électroniques sensibles dans les années 1960, il est devenu possible de mesurer les détails fins de la distribution d'énergie totale. Ceux-ci reflètent les détails fins de la physique des surfaces , et la technique de la spectroscopie électronique de champ a prospéré pendant un certain temps, avant d'être remplacée par de nouvelles techniques de science des surfaces.
Émetteurs d'électrons de champ comme sources de canons à électrons

Pour obtenir une haute résolution dans les microscopes électroniques et autres instruments à faisceau d'électrons (tels que ceux utilisés pour la lithographie par faisceau d'électrons ), il est utile de commencer avec une source d'électrons petite, optiquement brillante et stable. Les sources basées sur la géométrie d'un émetteur Mueller se qualifient bien sur les deux premiers critères. La première observation au microscope électronique (EM) d'un atome individuel a été réalisée par Crewe, Wall et Langmore en 1970, à l'aide d'un microscope électronique à balayage équipé d'un premier canon à émission de champ.
A partir des années 50, des efforts considérables ont été consacrés au développement de sources d'émission de champ à utiliser dans les canons à électrons . [par exemple, DD53] Des méthodes ont été développées pour générer des faisceaux sur l'axe, soit par accumulation d'émetteur induite par le champ, soit par dépôt sélectif d'un adsorbat à faible travail d' extraction (généralement de l' oxyde de zirconium - ZrO) dans l'apex plat de un émetteur en tungstène orienté (100) .
Les sources qui fonctionnent à température ambiante présentent l'inconvénient de se recouvrir rapidement de molécules d' adsorbat qui arrivent des parois du système de vide , et l'émetteur doit être nettoyé de temps en temps par « flash » à haute température. De nos jours, il est plus courant d'utiliser des sources à émetteur Mueller qui fonctionnent à des températures élevées, soit dans le régime d' émission de Schottky , soit dans ce que l'on appelle le régime intermédiaire de champ de température. De nombreux microscopes électroniques à haute résolution et instruments à faisceau d'électrons modernes utilisent une forme de source d'électrons basée sur un émetteur Mueller. Actuellement, des tentatives sont faites pour développer des nanotubes de carbone (CNT) comme sources d'émission de champ de canon à électrons.
L'utilisation de sources d'émission de champ dans les instruments d'optique électronique a impliqué le développement de théories appropriées de l'optique des particules chargées et le développement de la modélisation associée. Divers modèles de forme ont été essayés pour les émetteurs Mueller ; le meilleur semble être le modèle "Sphere on Orthogonal Cone" (SOC) introduit par Dyke, Trolan. Dolan et Barnes en 1953. Des simulations importantes, impliquant le traçage de trajectoire à l'aide du modèle d'émetteur SOC, ont été réalisées par Wiesener et Everhart. De nos jours, la possibilité de simuler l'émission de champ des émetteurs Mueller est souvent intégrée aux programmes commerciaux d'optique électronique utilisés pour concevoir des instruments à faisceau d'électrons. La conception de canons à électrons modernes et efficaces à émission de champ nécessite une expertise hautement spécialisée.
Émetteurs atomiquement pointus
De nos jours, il est possible de préparer des émetteurs très pointus, y compris des émetteurs qui se terminent par un seul atome. Dans ce cas, l'émission d'électrons provient d'une zone d'environ deux fois la taille cristallographique d'un seul atome. Cela a été démontré en comparant les images FEM et au microscope ionique de champ (FIM) de l'émetteur. Les émetteurs Mueller à un seul atome sont également pertinents pour la microscopie à sonde à balayage et la microscopie ionique à balayage à l'hélium (He SIM). Les techniques pour les préparer sont à l'étude depuis de nombreuses années. Une avancée récente importante connexe a été le développement (pour une utilisation dans le He SIM) d'une technique automatisée pour restaurer un sommet à trois atomes ("trimère") à son état d'origine, si le trimère se brise.
Sources d'émission de champ à grande surface : nanoélectronique sous vide
Aspects matériaux
Les sources d'émission de champ à grande surface suscitent l'intérêt depuis les années 1970. Dans ces dispositifs, une forte densité de sites d'émission de champ individuels est créée sur un substrat (à l'origine du silicium). Ce domaine de recherche est devenu connu, d'abord sous le nom de "microélectronique sous vide", maintenant sous le nom de "nanoélectronique sous vide".
L'un des deux types de dispositifs originaux, le « réseau de Spindt », utilisait des techniques de fabrication de circuits intégrés au silicium (CI) pour fabriquer des réseaux réguliers dans lesquels des cônes de molybdène étaient déposés dans de petits vides cylindriques dans un film d'oxyde, le vide étant recouvert d'un contre-électrode avec une ouverture circulaire centrale. Cette géométrie globale a également été utilisée avec des nanotubes de carbone cultivés dans le vide.
L'autre type d'appareil d'origine était le « émetteur Latham ». Il s'agissait de dispositifs MIMIV (métal-isolant-métal-isolant-vide) - ou, plus généralement, CDDCV (conducteur-diélectrique-conducteur-diélectrique-vide) - qui contenaient des particules conductrices dans un film diélectrique. L'appareil émet du champ parce que sa microstructure/nanostructure a des propriétés d'amélioration du champ. Ce matériau présentait un avantage potentiel de production, en ce sens qu'il pouvait être déposé sous forme d'« encre », de sorte que les techniques de fabrication de circuits intégrés n'étaient pas nécessaires. Cependant, dans la pratique, des dispositifs uniformément fiables se sont avérés difficiles à fabriquer.
La recherche a progressé pour rechercher d'autres matériaux qui pourraient être déposés/cultivés sous forme de films minces avec des propriétés d'amélioration de champ appropriées. Dans un arrangement à plaques parallèles, le champ "macroscopique" F M entre les plaques est donné par F M = V / W , où W est la séparation des plaques et V est la tension appliquée. Si un objet pointu est créé sur une plaque, alors le champ local F à son sommet est supérieur à F M et peut être lié à F M par
Le paramètre γ est appelé le « facteur d'accroissement de champ » et est essentiellement déterminée par la forme de l'objet. Étant donné que les caractéristiques d'émission de champ sont déterminés par le champ local F , puis plus le γ -valeur de l'objet, puis plus la valeur de F M au cours de laquelle se produit l' émission importante. Par conséquent, pour une valeur donnée de W , plus la tension appliquée V à laquelle une émission significative se produit est faible .
Pendant une période d'environ dix ans à partir du milieu des années 1990, il y avait un grand intérêt pour l'émission de champ à partir de films déposés par plasma de carbone amorphe et "diamant" . Cependant, l'intérêt a diminué par la suite, en partie en raison de l'arrivée d' émetteurs de NTC , et en partie parce que des preuves ont émergé que les sites d'émission pourraient être associés à des objets de carbone particulaire créés d'une manière inconnue au cours du processus de dépôt : cela a suggéré que le contrôle qualité d'un processus de production à grande échelle pourrait être problématique.
L'introduction d'émetteurs de champ CNT, à la fois sous forme de "mat" et sous forme de "matrice cultivée", a été un pas en avant significatif. Des recherches approfondies ont été entreprises à la fois sur leurs caractéristiques physiques et leurs applications technologiques possibles. Pour l'émission de champ, un avantage des NTC est que, en raison de leur forme, avec son rapport d'aspect élevé , ce sont des "objets naturels améliorant le champ".
Ces dernières années, il y a également eu une croissance massive de l'intérêt pour le développement d'autres formes d'émetteurs à couches minces, à la fois celles basées sur d'autres formes de carbone (telles que les « nanowalls de carbone ») et sur diverses formes de semi-conducteurs à large bande interdite. Un but particulier est de développer « haute gamma nanostructures » avec une densité suffisamment élevée de sites d'émission individuelles. Des films minces de nanotubes sous forme de nappes de nanotubes sont également utilisés pour le développement d'électrodes à émission de champ. Il est montré qu'en ajustant finement les paramètres de fabrication, ces nappes peuvent atteindre une densité optimale de sites d'émission individuels. allumer un champ électrique (champ électrique requis pour atteindre un courant d'émission de 10 A/cm 2 ) jusqu'à 0,3 V/μm et fournir une performance d'émission de champ stable.
Les problèmes communs à tous les dispositifs d'émission de champ, en particulier ceux qui fonctionnent dans des "conditions de vide industriel", sont que les performances d'émission peuvent être dégradées par l'adsorption d'atomes de gaz provenant d'ailleurs dans le système, et la forme de l'émetteur peut en principe être modifiée de manière délétère. par une variété de processus secondaires indésirables, tels que le bombardement par des ions créés par l'impact des électrons émis sur les atomes en phase gazeuse et/ou sur la surface des contre-électrodes. Ainsi, une exigence industrielle importante est la "robustesse dans de mauvaises conditions de vide" ; ceci doit être pris en compte dans les recherches sur les nouveaux matériaux émetteurs.
Au moment de la rédaction, les formes les plus prometteuses de source d'émission de champ à grande surface (certainement en termes de densité de courant d'émission moyenne atteinte) semblent être les réseaux de Spindt et les différentes formes de source basées sur les NTC.
Applications
Le développement de sources d'émission de champ à grande surface était à l'origine motivé par le souhait de créer de nouvelles formes plus efficaces d' affichage électronique de l'information . Ceux-ci sont appelés « écrans à émission de champ » ou « écrans nano-émissifs ». Bien que plusieurs prototypes aient été démontrés, le développement de tels écrans en produits commerciaux fiables a été entravé par une variété de problèmes de production industrielle non directement liés aux caractéristiques de la source [En08].
D'autres applications proposées de sources d'émission de champ à grande surface comprennent la génération de micro - ondes , la neutralisation de véhicules spatiaux, la génération de rayons X et (pour les sources matricielles) la lithographie à faisceaux électroniques multiples . Il existe également des tentatives récentes pour développer des émetteurs à grande surface sur des substrats flexibles, en ligne avec les tendances plus larges vers « l' électronique plastique ».
Le développement de telles applications est la mission de la nanoélectronique sous vide. Cependant, les émetteurs de champ fonctionnent mieux dans des conditions de bon ultravide. Leurs applications les plus réussies à ce jour (pistolets FEM, FES et EM) ont eu lieu dans ces conditions. Il n'en reste pas moins triste que les émetteurs de champ et les conditions de vide industriel ne font pas bon ménage, et les problèmes liés à assurer de manière fiable une bonne "robustesse au vide" des sources d'émission de champ utilisées dans de telles conditions attendent toujours de meilleures solutions (probablement des solutions de matériaux plus intelligentes) que celles que nous connaissons actuellement. ont.
Phénomènes de claquage du vide et de décharge électrique
Comme déjà indiqué, on pense maintenant que les premières manifestations de l'émission d'électrons de champ étaient les décharges électriques qu'elle provoquait. Après les travaux de Fowler-Nordheim, il a été compris que la CFE était l'une des principales causes sous-jacentes possibles des phénomènes de claquage du vide et de décharge électrique. (Les mécanismes détaillés et les voies impliquées peuvent être très compliqués, et il n'y a pas de cause universelle unique) Lorsque la rupture du vide est connue pour être causée par l'émission d'électrons d'une cathode, alors la pensée originale était que le mécanisme était CFE à partir d'une petite aiguille conductrice. comme des saillies de surface. Des procédures ont été (et sont) utilisées pour arrondir et lisser les surfaces des électrodes qui pourraient générer des courants d'émission d'électrons de champ indésirables. Cependant, les travaux de Latham et d'autres ont montré que l'émission pouvait également être associée à la présence d'inclusions semi-conductrices dans les surfaces lisses. La physique de la façon dont l'émission est générée n'est toujours pas entièrement comprise, mais on soupçonne que les soi-disant "effets de triple jonction" peuvent être impliqués. De plus amples informations peuvent être trouvées dans le livre de Latham et dans la bibliographie en ligne.
Transfert d'électrons interne dans les appareils électroniques
Dans certains appareils électroniques, le transfert d'électrons d'un matériau à un autre, ou (dans le cas de bandes inclinées) d'une bande à une autre (« Zener tunneling »), s'effectue par un processus d'effet tunnel induit par le champ qui peut être considéré comme une forme du tunnel Fowler-Nordheim. Par exemple, le livre de Rhoderick traite de la théorie relative aux contacts métal-semi-conducteur .
Tunnel Fowler–Nordheim
introduction
La partie suivante de cet article traite de la théorie de base de l'émission d'électrons en champ froid à partir de métaux en vrac. Ceci est mieux traité en quatre étapes principales, impliquant la théorie associée à : (1) la dérivation d'une formule pour la « probabilité d'échappement », en considérant l'effet tunnel d'électrons à travers une barrière triangulaire arrondie ; (2) une intégration sur les états électroniques internes pour obtenir la "distribution d'énergie totale" ; (3) une seconde intégration, pour obtenir la densité de courant d'émission en fonction du champ barrière local et du travail de sortie local ; (4) conversion de ceci en une formule pour le courant en fonction de la tension appliquée. Les équations modifiées nécessaires pour les émetteurs de grande surface et les problèmes d'analyse des données expérimentales sont traités séparément.
L'effet tunnel de Fowler-Nordheim est l' effet tunnel mécanique d'onde d'un électron à travers une barrière triangulaire exacte ou arrondie. Deux situations de base sont reconnues : (1) lorsque l'électron est initialement dans un état localisé ; (2) lorsque l'électron n'est initialement pas fortement localisé, et est mieux représenté par une onde progressive . L'émission d'une bande de conduction de métal massif est une situation du deuxième type, et la discussion ici se rapporte à ce cas. On suppose également que la barrière est unidimensionnelle (c'est-à-dire qu'elle n'a pas de structure latérale) et qu'elle n'a pas de structure à petite échelle qui provoque des effets de « diffusion » ou de « résonance ». Pour que cette explication de l'effet tunnel de Fowler-Nordheim reste relativement simple, ces hypothèses sont nécessaires ; mais la structure atomique de la matière est en effet négligée.
Énergie motrice
Pour un électron, l' équation de Schrödinger à une dimension peut être écrite sous la forme
-
( 1 )
où ( x ) est la fonction d'onde des électrons , exprimée en fonction de la distance x mesurée à partir de la surface électrique de l'émetteur, ħ est la constante de Planck réduite , m est la masse des électrons, U ( x ) est l' énergie potentielle des électrons , E n est l' énergie totale des électrons associée au mouvement dans la direction x , et M ( x ) = [ U ( x ) − E n ] est appelée l'énergie motrice des électrons. M ( x ) peut être interprété comme le négatif de l'énergie cinétique électronique associée au mouvement d'un hypothétique électron ponctuel classique dans la direction x , et est positif dans la barrière.
La forme d'une barrière tunnel est déterminée par la façon dont M ( x ) varie avec la position dans la région où M ( x ) > 0. Deux modèles ont un statut particulier dans la théorie de l'émission de champ : la barrière triangulaire exacte (ET) et la barrière Schottky-Nordheim barrière (SN) . Ceux-ci sont donnés par les équations (2) et (3), respectivement :
-
( 2 )
-
( 3 )
Ici h est la hauteur en champ nul (ou hauteur non réduite ) de la barrière, e est la charge positive élémentaire , F est le champ de barrière, et ε 0 est la constante électrique . Par convention, F est pris comme positif, même si le champ électrostatique classique serait négatif. L'équation SN utilise l'énergie potentielle d'image classique pour représenter l'effet physique « corrélation et échange ».
Probabilité de fuite
Pour un électron s'approchant de l'intérieur d'une barrière donnée, la probabilité de fuite (ou « coefficient de transmission » ou « coefficient de pénétration ») est fonction de h et F , et est notée D ( h , F ). L'objectif principal de la théorie de l'effet tunnel est de calculer D ( h , F ). Pour les modèles de barrières physiquement réalistes, tels que la barrière de Schottky-Nordheim, l' équation de Schrödinger ne peut pas être résolue exactement de manière simple. L'approche dite "semi-classique" suivante peut être utilisée. Un paramètre G ( h , F ) peut être défini par l' intégrale JWKB (Jeffreys-Wentzel-Kramers-Brillouin) :
-
( 4 )
où l'intégrale est prise à travers la barrière (c'est-à-dire à travers la région où M > 0), et le paramètre g est une constante universelle donnée par
-
( 5 )
Forbes a réarrangé un résultat prouvé par Fröman et Fröman, pour montrer que, formellement - dans un traitement unidimensionnel - la solution exacte pour D peut être écrite
-
( 6 )
où le préfacteur d'effet tunnel P peut en principe être évalué par des intégrations itératives compliquées le long d'un chemin dans un espace complexe . Dans le régime CFE nous avons (par définition) G 1. Aussi, pour les modèles simples P 1. Donc l'éq. (6) se réduit à la formule JWKB dite simple :
-
( 7 )
Pour la barrière triangulaire exacte, mettre l'éq. (2) dans l'éq. (4) donne G ET = bh 3/2 / F , où
-
( 8 )
Ce paramètre b est une constante universelle parfois appelée la deuxième constante de Fowler-Nordheim . Pour les barrières d'autres formes, nous écrivons
-
( 9 )
où ν ( h , F ) est un facteur de correction qui , en général doit être déterminée par intégration numérique , en utilisant l' équation. (4).
Facteur de correction pour la barrière Schottky-Nordheim
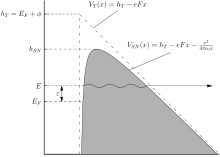
La barrière de Schottky-Nordheim, qui est le modèle de barrière utilisé pour dériver l'équation standard de type Fowler-Nordheim, est un cas particulier. Dans ce cas, on sait que le facteur de correction est fonction d'une seule variable f h , définie par f h = F / F h , où F h est le champ nécessaire pour réduire la hauteur d'une barrière Schottky-Nordheim de h à 0. Ce champ est donné par
-
( 10 )
Le paramètre f h va de 0 à 1, et peut être appelé champ de barrière mis à l' échelle , pour une barrière Schottky-Nordheim de hauteur de champ zéro h .
Pour la barrière Schottky-Nordheim, ν ( h , F ) est donné par la valeur particulière ν ( f h ) d'une fonction ν ( ℓ′ ). Cette dernière est une fonction de la physique mathématique à part entière et a été appelée la principale fonction barrière de Schottky-Nordheim . Un développement explicite en série pour ν ( ℓ′ ) est dérivé dans un article de 2008 de J. Deane. La bonne approximation simple suivante pour ν ( f h ) a été trouvée :
-
( 11 )
Largeur de pourriture
La largeur de décroissance (en énergie), d h , mesure la vitesse à laquelle la probabilité d'échappement D diminue à mesure que la hauteur de barrière h augmente; d h est défini par:
-
( 12 )
Lorsque h augmente de d h alors la probabilité d'évasion D diminue d'un facteur proche de e ( ≈ 2,718282). Pour un modèle élémentaire, basé sur la barrière triangulaire exacte, où l'on met ν = 1 et P ≈ 1, on obtient
La décroissance de largeur d h dérivé de l'expression plus générale (12) diffère de cela par un « facteur de correction décroissance de largeur » λ d , de sorte que :
-
( 13 )
Habituellement, le facteur de correction peut être approximé comme l'unité.
La largeur de décroissance d F pour une barrière avec h égal à la fonction de travail locale φ est particulièrement intéressante. Numériquement, cela est donné par :
-
( 14 )
Pour les métaux, la valeur de d F est typiquement de l'ordre de 0,2 eV, mais varie avec le champ barrière F .
commentaires
Une note historique s'impose. L'idée que la barrière Schottky-Nordheim avait besoin d'un facteur de correction, comme dans l'éq. (9), a été introduit par Nordheim en 1928, mais son analyse mathématique du facteur était incorrecte. Une nouvelle fonction (correcte) a été introduite par Burgess, Kroemer et Houston en 1953, et ses mathématiques ont été développées plus avant par Murphy et Good en 1956. Cette fonction corrigée, parfois connue sous le nom de "fonction elliptique à émission de champ spécial", a été exprimée sous la forme d'une fonction d'une variable mathématique y appelée « paramètre de Nordheim ». Ce n'est que récemment (2006 à 2008) qu'on s'est rendu compte que, mathématiquement, il est bien préférable d'utiliser la variable ℓ′ ( = y 2 ) . Et ce n'est que récemment qu'il a été possible de compléter la définition de ν ( ℓ′ ) en développant et en prouvant la validité d'un développement en série exact pour cette fonction (en partant de solutions de cas particuliers connues de l' équation différentielle hypergéométrique de Gauss ). De plus, l'approximation (11) n'a été trouvée que récemment. L'approximation (11) surpasse, et finira vraisemblablement par remplacer, toutes les anciennes approximations de complexité équivalente. Ces développements récents, et leurs implications, auront probablement un impact significatif sur la recherche sur les émissions sur le terrain en temps voulu.
Le résumé suivant rassemble ces résultats. Pour creuser un tunnel bien en dessous du sommet d'une barrière bien élevée de hauteur raisonnable, la probabilité de fuite D ( h , F ) est donnée formellement par :
-
( 15 )
où ν ( h , F ) est un facteur de correction qui , en général doit être trouvée par intégration numérique. Pour le cas particulier d'une barrière Schottky-Nordheim, un résultat analytique existe et ν ( h , F ) est donné par ν ( f h ), comme discuté ci-dessus ; l'approximation (11) pour ν ( f h ) est plus que suffisante pour tous les objectifs technologiques. Le préfacteur P est également en principe fonction de h et (peut-être) F , mais pour les modèles physiques simples discutés ici, il est généralement satisfaisant de faire l'approximation P = 1. La barrière triangulaire exacte est un cas particulier où le Schrödinger l'équation peut être résolue exactement, comme l'ont fait Fowler et Nordheim ; pour ce cas physiquement irréaliste, ν ( f h ) = 1, et une approximation analytique pour P existe.
L'approche décrite ici a été développée à l'origine pour décrire l'effet tunnel de Fowler-Nordheim à partir de surfaces d'émission planes, lisses et classiques. Il convient aux surfaces courbes lisses classiques de rayons allant jusqu'à environ 10 à 20 nm. Elle peut être adaptée à des surfaces de rayon plus aigu, mais des quantités telles que ν et D deviennent alors des fonctions significatives du ou des paramètres utilisés pour décrire la courbure de la surface. Lorsque l'émetteur est si précis que les détails au niveau atomique ne peuvent pas être négligés, et/ou que la barrière tunnel est plus épaisse que les dimensions du sommet de l'émetteur, une approche plus sophistiquée est alors souhaitable.
Comme indiqué au début, les effets de la structure atomique des matériaux ne sont pas pris en compte dans les traitements relativement simples de l'émission d'électrons de champ discutés ici. La prise en compte correcte de la structure atomique est un problème très difficile, et seuls des progrès limités ont été réalisés. Cependant, il semble probable que les principales influences sur la théorie de l' effet tunnel Fowler-Nordheim seront (en vigueur) est de modifier les valeurs de P et v dans l' équation. (15), par des montants qui ne peuvent être facilement estimés à l'heure actuelle.
Toutes ces remarques s'appliquent en principe à l'effet tunnel de Fowler Nordheim à partir de n'importe quel conducteur où (avant l'effet tunnel) les électrons peuvent être traités comme dans des états d'ondes progressives . L'approche peut être adaptée pour s'appliquer (approximativement) à des situations où les électrons sont initialement dans des états localisés à ou très près à l'intérieur de la surface émettrice, mais cela dépasse le cadre de cet article.
Distribution d'énergie totale
La distribution d'énergie des électrons émis est importante à la fois pour les expériences scientifiques qui utilisent la distribution d'énergie des électrons émis pour sonder les aspects de la physique de la surface de l'émetteur et pour les sources d'émission de champ utilisées dans les instruments à faisceau d'électrons tels que les microscopes électroniques . Dans ce dernier cas, la "largeur" (en énergie) de la distribution influence la finesse de focalisation du faisceau.
L'explication théorique suit ici l'approche de Forbes. Si ε désigne l' énergie électronique totale par rapport à l'émetteur de niveau de Fermi, et K p désigne l' énergie cinétique de la parallèle d'électrons à la surface d'émetteur, puis de l'électron d' énergie normale ε n (parfois appelé son « énergie vers l' avant ») est défini par
-
( 16 )
Deux types de distribution d'énergie théorique sont reconnus : la distribution d'énergie normale (NED), qui montre comment l'énergie ε n est distribuée immédiatement après l'émission (c'est-à-dire immédiatement à l'extérieur de la barrière tunnel) ; et la distribution totale d'énergie , ce qui montre comment l'énergie totale ε est distribuée. Lorsque le niveau de Fermi émetteur est utilisé comme le niveau zéro de référence, à la fois ε et ε n peuvent être soit positive ou négative.
Des expériences d'analyse énergétique sont réalisées sur des émetteurs de champ depuis les années 1930. Cependant, ce n'est qu'à la fin des années 1950 qu'on s'est rendu compte (par Young et Mueller [,YM58]) que ces expériences mesuraient toujours la distribution d'énergie totale, qui est maintenant généralement notée j ( ε ). Ceci est également vrai (ou presque vrai) lorsque l'émission provient d'une petite saillie améliorant le champ sur une surface par ailleurs plate.
Pour voir comment la distribution de l'énergie totale peut être calculée dans le cadre d'un modèle de type électrons libres de Sommerfeld , regardez le diagramme énergie-espace PT (PT="parallel-total").
Ceci montre la « parallèle énergie cinétique » K p sur l'axe horizontal et l' énergie totale e sur l'axe vertical. Un électron à l' intérieur du métal en vrac a généralement des valeurs de K p et e qui se trouvent dans la zone légèrement ombragée. On peut montrer que chaque élément d ε d K p de cet espace d'énergie apporte une contribution à la constatation de la densité de courant d'électrons à l'intérieur de la limite d'émetteur. Ici, z S est la constante universelle (appelée ici la densité d'offre de Sommerfeld ) :
-
( 17 )
et est la fonction de distribution de Fermi-Dirac :
-
( 18 )
où T est la température thermodynamique et k B est la constante de Boltzmann .
Cet élément de densité de courant incident voit une barrière de hauteur h donnée par :
-
( 19a )
La probabilité d'échappement correspondante est D ( h , F ) : elle peut être développée (approximativement) sous la forme
-
( 19b )
où D F est la probabilité d'échappement pour un obstacle de hauteur non réduite égale à la fonction de travail locale φ . Par conséquent, l'élément d ε d K p apporte une contribution à la densité de courant d' émission, et la contribution totale des électrons incidents avec des énergies dans la gamme de d élémentaire ε est donc
-
( 20 )
où l'intégrale est en principe prise le long de la bande représentée sur le schéma, mais peut en pratique être étendue à ∞ lorsque la largeur de décroissance d F est très inférieure à l' énergie de Fermi K F (ce qui est toujours le cas pour un métal) . Le résultat de l'intégration peut s'écrire :
-
( 21 )
où et sont des valeurs appropriées pour une barrière de hauteur non réduite h égale à la fonction de travail locale φ et est définie par l'équation.
Pour un émetteur donné, avec un champ donné qui lui est appliqué, est indépendant de F , donc l'éq. (21) montre que la forme de la distribution (à mesure que ε augmente à partir d'une valeur négative bien en dessous du niveau de Fermi) est une exponentielle croissante, multipliée par la fonction de distribution FD . Cela génère la forme de distribution familière d'abord prédite par Young. Aux basses températures, passe brusquement de 1 à 0 au voisinage du niveau de Fermi, et la FWHM de la distribution est donnée par :
-
( 22 )
Le fait que les distributions expérimentales d'énergie totale de CFE aient cette forme de base est une bonne confirmation expérimentale que les électrons dans les métaux obéissent à la statistique de Fermi-Dirac .
Emission d'électrons en champ froid
Équations de type Fowler-Nordheim
introduction
Les équations de type Fowler-Nordheim, sous la forme J - F , sont des équations théoriques (approximatives) dérivées pour décrire la densité de courant locale J émise par les états électroniques internes dans la bande de conduction d'un métal massif. La densité de courant d' émission (ECD) J pour une région de petit uniforme d'une surface d' émission est généralement exprimée en fonction J ( φ , F ) de la fonction de travail locale φ et le champ barrière locale F qui caractérise la petite région. Pour les surfaces fortement incurvées, J peut également dépendre du ou des paramètres utilisés pour décrire la courbure de la surface.
En raison des hypothèses physiques faites dans la dérivation originale, le terme équation de type Fowler-Nordheim a longtemps été utilisé uniquement pour les équations qui décrivent l'ECD à température zéro. Cependant, il est préférable d'autoriser ce nom à inclure les équations légèrement modifiées (discutées ci-dessous) qui sont valables pour des températures finies dans le régime d'émission CFE.
Forme à température nulle
La densité de courant est mieux mesurée en A/m 2 . La densité de courant totale émise à partir d' une petite région uniforme peut être obtenue en intégrant la distribution d'énergie totale j ( ε ) par rapport à l' énergie des électrons totale ε . A température nulle, la fonction de distribution de Fermi-Dirac f FD = 1 pour ε <0, et f FD = 0 pour ε > 0. Ainsi, l'ECD à 0 K, J 0 , est donné à partir de l'éq. (18) par
-
( 23 )
où est l' offre effective pour l'état F , et est définie par cette équation. Strictement, la limite inférieure de l'intégrale devrait être − K F , où K F est l' énergie de Fermi ; mais si d F est très inférieur à K F (ce qui est toujours le cas pour un métal) alors aucune contribution significative à l'intégrale ne vient des énergies inférieures à K F , et elle peut être formellement étendue à –∞.
Le résultat (23) peut recevoir une interprétation physique simple et utile en se référant à la figure 1. L'état électronique au point "F" sur le diagramme ("état F") est "l'état de déplacement vers l'avant au niveau de Fermi" (c'est-à-dire , il décrit un électron de niveau de Fermi se déplaçant normalement vers et vers la surface de l'émetteur). A 0 K, un électron dans cet état voit une barrière de hauteur non réduite φ , et a une probabilité de fuite D F qui est supérieure à celle de tout autre état électronique occupé. Il est donc pratique d'écrire J 0 sous la forme Z F D F , où "l'alimentation effective" Z F est la densité de courant qui devrait être transportée par l'état F à l'intérieur du métal si toute l'émission sortait de l'état F.
En pratique, la densité de courant provient principalement d'un groupe d'états proches en énergie de l'état F, dont la plupart se situent dans la zone fortement ombrée du diagramme énergie-espace. Puisque, pour un modèle d'électrons libres , la contribution à la densité de courant est directement proportionnelle à la surface dans l'espace énergétique (avec la densité d'alimentation de Sommerfeld z S comme constante de proportionnalité), il est utile de penser à l'ECD comme tiré de états électroniques dans une zone de taille d F 2 (mesurée en eV 2 ) dans le diagramme énergie-espace. C'est-à-dire qu'il est utile de considérer l'ECD comme tiré des états dans la zone fortement ombrée de la figure 1. (Cette approximation s'aggrave lentement à mesure que la température augmente.)
Z F peut aussi s'écrire sous la forme :
-
( 24 )
où la constante universelle a , parfois appelée la première constante de Fowler-Nordheim , est donnée par
-
( 25 )
Cela montre clairement que le facteur pré-exponentiel un φ -1 F 2 , qui apparaît dans les équations Fowler-Nordheim de type, se rapporte à la fourniture efficace d'électrons à la surface d'émetteur, dans un modèle à électrons libres.
Températures non nulles
Pour obtenir un résultat valable pour une température non nulle, on note à partir de l'éq. (23) que z S d F D F = J 0 / d F . Ainsi, lorsque l'éq. (21) est intégré à température non nulle, alors – en faisant cette substitution, et en insérant la forme explicite de la fonction de distribution de Fermi–Dirac – l'ECD J peut s'écrire sous la forme :
-
( 26 )
où λ T est un facteur de correction de température donnée par l'intégrale. L'intégrale peut être transformée, en écrivant et , puis , en le résultat standard :
-
( 27 )
Ceci est valable pour w > 1 (c'est-à-dire d F / k B T > 1). Donc – pour des températures telles que k B T < d F :
-
( 28 )
où le développement n'est valide que si (π k B T / d F ) 1. Un exemple de valeur (pour φ = 4,5 eV, F = 5 V/nm, T = 300 K) est λ T = 1,024. Pensée normale a été que, dans le régime de CFE, λ T est toujours faible par rapport à d' autres incertitudes, et qu'il est généralement nécessaire d'inclure explicitement dans les formules pour la densité de courant à la température ambiante.
Les régimes d'émission pour les métaux sont, en pratique, définis par les gammes de champ barrière F et de température T pour lesquelles une famille donnée d'équations d'émission est mathématiquement adéquate. Lorsque le champ barrière F est suffisamment élevé pour que le régime CFE fonctionne pour une émission de métal à 0 K, alors la condition k B T < d F fournit une limite supérieure formelle (en température) au régime d'émission CFE. Cependant, il a été avancé que (en raison d'approximations faites ailleurs dans la dérivation) la condition k B T <0,7 d F est une meilleure limite de travail : cela correspond à une valeur λ T d'environ 1,09, et (pour le cas d'exemple ) une limite supérieure de température sur le régime CFE d'environ 1770 K. Cette limite est fonction du champ barrière.
Notez que le résultat (28) s'applique ici à une barrière de n'importe quelle forme (bien que d F soit différent pour différentes barrières).
Équation de type Fowler-Nordheim physiquement complète
Le résultat (23) conduit également à une certaine compréhension de ce qui se passe lorsque les effets au niveau atomique sont pris en compte et que la structure de bande n'est plus semblable à celle des électrons libres. En raison de la présence des noyaux ioniques atomiques, la barrière de surface, ainsi que les fonctions d'onde des électrons à la surface, seront différentes. Ceci affectera les valeurs du facteur de correction , le préfacteur P , et (dans une moindre mesure) le facteur de correction de la d . Ces changements affecteront à leur tour les valeurs du paramètre D F et (dans une mesure limitée) du paramètre d F . Pour un métal réel, la densité d'alimentation variera avec la position dans l'espace énergétique, et la valeur au point "F" peut être différente de la densité d'alimentation de Sommerfeld. Nous pouvons prendre en compte cet effet en introduisant un facteur de correction de structure de bande électronique λ B dans l'éq. (23). Modinos a expliqué comment ce facteur pourrait être calculé : il estime qu'il se situe le plus probablement entre 0,1 et 1 ; il peut se situer en dehors de ces limites, mais il est très peu probable qu'il se situe en dehors de la plage 0,01< λ B <10.
En définissant un facteur global de correction de l'offre λ Z égal à λ T λ B λ d 2 , et en combinant les équations ci-dessus, on arrive à l'équation dite physiquement complète de type Fowler-Nordheim :
-
( 29 )
où [= ( φ , F )] est le facteur de correction d'exposant pour une barrière de hauteur non réduite φ . C'est l'équation la plus générale du type Fowler-Nordheim. D' autres équations dans la famille sont obtenues en remplaçant les expressions spécifiques pour les trois facteurs de correction , P F et λ Z contient. L'équation dite élémentaire de type Fowler-Nordheim, qui apparaît dans les discussions des manuels de premier cycle sur l'émission de champ, est obtenue en mettant λ Z →1, P F →1, →1; cela ne donne pas de bonnes prédictions quantitatives car cela rend la barrière plus solide qu'elle ne l'est dans la réalité physique. L'équation dite standard de type Fowler-Nordheim, développée à l'origine par Murphy et Good, et très utilisée dans la littérature passée, est obtenue en mettant λ Z → t F −2 , P F →1, → v F , où v F est v ( f ), où f est la valeur de f h obtenue en mettant h = φ , et t F est un paramètre lié (de valeur voisine de l' unité).
De plus théorie complète décrite ici, le facteur t F -2 est une partie composante du facteur de correction de la d 2 [voir, et notez que λ d 2 est désignée par λ D y]. Il n'y a aucune valeur significative à poursuivre l'identification séparée de t F -2 . Probablement, dans l'état actuel des connaissances, la meilleure approximation pour une modélisation simple basée sur des équations de type Fowler-Nordheim de CFE à partir de métaux est obtenue en mettant λ Z →1, P F → 1, → v ( f ). Cela régénère l'équation de type Fowler-Nordheim utilisée par Dyke et Dolan en 1956, et peut être appelée "l'équation standard simplifiée de type Fowler-Nordheim".
Forme recommandée pour les calculs simples de type Fowler-Nordheim
Explicitement, cette équation standard simplifiée de type Fowler-Nordheim recommandée , et les formules associées, sont :
-
( 30a )
-
( 30b )
-
( 30c )
-
( 30j )
où F & phiv ici est le champ nécessaire pour réduire à zéro une barrière Schottky-Nordheim de hauteur non réduite égale à la fonction de travail locale φ , et f est le champ barrière mise à l' échelle pour une barrière Schottky-Nordheim de hauteur non réduite φ . [Cette quantité f aurait pu être écrit plus exactement comme f φ SN , mais il rend cette équation Fowler-type Nordheim look moins si la convention encombraient est adoptée si simple f signifie la quantité notée f φ SN dans, éq. (2,16)] Dans le cas de l' exemple (. Φ = 4,5 eV, F = 5 V / nm), f ≈ 0,36 et v ( f ) ≈ 0,58; les plages pratiques pour ces paramètres sont discutées plus loin.
Notez que la variable f (le champ barrière mis à l'échelle) n'est pas la même que la variable y (le paramètre de Nordheim) largement utilisée dans la littérature sur les émissions de champ antérieures, et que " v ( f ) " n'a PAS la même signification mathématique et les mêmes valeurs que la quantité " v ( y ) " qui apparaît dans la littérature sur les émissions de champ. Dans le contexte de la théorie révisée décrite ici, les formules pour v ( y ) et les tableaux de valeurs pour v ( y ) doivent être ignorés ou traités comme des valeurs de v ( f 1/2 ). Si des valeurs plus exactes pour v ( f ) sont requises, alors fournit des formules qui donnent des valeurs pour v ( f ) avec une précision mathématique absolue meilleure que 8×10 -10 . Cependant, la formule d'approximation (30c) ci-dessus, qui donne des valeurs correctes avec une précision mathématique absolue supérieure à 0,0025, devrait donner des valeurs suffisamment précises pour tous les objectifs technologiques.
commentaires
Une note historique sur les méthodes de dérivation des équations de type Fowler-Nordheim est nécessaire. Il existe plusieurs approches possibles pour dériver ces équations, en utilisant la théorie des électrons libres . L'approche utilisée ici a été introduite par Forbes en 2004 et peut être décrite comme "l'intégration via la distribution d'énergie totale, en utilisant l'énergie cinétique parallèle K p comme première variable d'intégration". Fondamentalement, il s'agit d'un équivalent en électrons libres de la procédure de Modinos (dans un traitement de mécanique quantique plus avancé) d'« intégration sur la zone de Brillouin de surface ». En revanche, les traitements à électrons libres de CFE de Young en 1959, Gadzuk et Plummer en 1973 et Modinos en 1984, intègrent également par la distribution totale d'énergie, mais utilisent l'énergie normale ε n (ou une quantité correspondante) comme la première variable d'intégration.
Il existe également une approche plus ancienne, basée sur un article fondateur de Nordheim en 1928, qui formule le problème différemment et utilise ensuite d'abord K p puis ε n (ou une quantité apparentée) comme variables d'intégration : c'est ce qu'on appelle « l'intégration via la distribution d'énergie normale". Cette approche continue d'être utilisée par certains auteurs. Bien qu'il présente certains avantages, en particulier lorsqu'il s'agit de discuter des phénomènes de résonance, il nécessite l'intégration de la fonction de distribution de Fermi-Dirac dans la première étape d'intégration : pour les structures de bande électroniques de type non libre, cela peut conduire à des erreurs très complexes et mathématiques sujettes (comme dans les travaux de Stratton sur les semi-conducteurs ). De plus, l'intégration via la distribution d'énergie normale ne génère pas de distributions d'énergie électronique mesurées expérimentalement.
En général, l'approche utilisée ici semble plus facile à comprendre, et conduit à des mathématiques plus simples.
Il est également plus proche en principe des approches plus sophistiquées utilisées lorsqu'il s'agit de solides cristallins en vrac réels, où la première étape consiste soit à intégrer les contributions à l'ECD sur des surfaces à énergie constante dans un espace vectoriel d'onde ( espace k ), soit à intégrer les apports sur la zone Brillouin de surface pertinente. L'approche de Forbes équivaut soit à intégrer sur une surface sphérique dans l' espace k , en utilisant la variable K p pour définir un élément d'intégration en forme d'anneau qui a une symétrie cylindrique autour d'un axe dans une direction normale à la surface émettrice, soit à intégrer sur une zone Brillouin de surface (étendue) utilisant des éléments annulaires circulaires.
Equations théoriques CFE
La section précédente explique comment dériver des équations de type Fowler-Nordheim. Strictement, ces équations ne s'appliquent qu'aux CFE à partir de métaux en vrac. Les idées dans les sections suivantes s'appliquent à CFE plus généralement, mais l'éq. (30) servira à les illustrer.
Pour CFE, les traitements théoriques de base fournissent une relation entre la densité de courant d'émission locale J et le champ barrière local F , à une position locale sur la surface émettrice. Les expériences mesurent le courant d'émission i à partir d'une partie définie de la surface d'émission, en fonction de la tension V appliquée à une contre-électrode. Pour relier ces variables à J et F , des équations auxiliaires sont utilisées.
Le facteur de conversion tension-barrière à champ β est défini par:
-
( 31 )
La valeur de F varie d' une position à sur une surface d'émetteur, et la valeur de β varie de façon correspondante.
Pour un émetteur métallique, la valeur de β pour une position donnée sera constante (indépendamment de la tension) dans les conditions suivantes : (1) l'appareil est un arrangement de "diode", où les seules électrodes présentes sont l'émetteur et un ensemble de « environnement », dont toutes les parties sont à la même tension ; (2) aucune charge d'espace dans le vide émise par champ significatif (FEVSC) n'est présente (cela sera vrai sauf à des densités de courant d'émission très élevées, autour de 10 9 A/m 2 ou plus) ; (3) il n'existe pas de « champs de correction » significatifs, en raison de non-uniformités dans la fonction de travail locale (cela est normalement supposé être vrai, mais peut ne pas l'être dans certaines circonstances). Pour les non-métaux, les effets physiques appelés « pénétration de champ » et « flexion de bande » [M084] peuvent faire de β une fonction de la tension appliquée, bien que – étonnamment – il existe peu d'études sur cet effet.
La densité de courant d'émission J varie d'une position à l'autre sur la surface de l'émetteur. Le courant d'émission total i d'une partie définie de l'émetteur est obtenu en intégrant J à travers cette partie. Pour obtenir une équation simple pour i ( V ), la procédure suivante est utilisée. Un point de référence « R » est choisi à l'intérieur de cette partie de la surface d'émetteur (souvent le point auquel la densité de courant est la plus élevée), et la densité de courant à ce point de référence est désigné par J r . Un paramètre A r , appelé zone d'émission notionnelle (par rapport au point "r"), est alors défini par :
-
( 32 )
où l'intégrale est prise à travers la partie de l'émetteur d'intérêt.
Ce paramètre A r a été introduit dans la théorie CFE par Stern, Gossling et Fowler en 1929 (qui l'appelaient une "zone moyenne pondérée"). Pour les émetteurs pratiques, la densité de courant d'émission utilisée dans les équations de type Fowler-Nordheim est toujours la densité de courant à un point de référence (bien que cela ne soit généralement pas indiqué). Convention établie de longue date indique cette référence densité de courant par le simple symbole J , et le champ local et facteur de conversion correspondant par les symboles simples F et β , sans l'indice « r » utilisé ci - dessus; dans ce qui suit, cette convention est utilisée.
La zone d'émission théorique A r sera souvent fonction du champ local de référence (et donc de la tension) et, dans certaines circonstances, pourrait être une fonction significative de la température.
Parce que A r a une définition mathématique, il ne correspond pas nécessairement à la zone à partir de laquelle l'émission est observée à partir d'un émetteur ponctuel dans un microscope électronique de champ (émission) . Avec un émetteur de grande surface, qui contient de nombreux sites d'émission individuels, A r sera presque toujours très très inférieur à la surface géométrique « macroscopique » ( A M ) de l'émetteur telle qu'observée visuellement (voir ci-dessous).
L'incorporation de ces équations auxiliaires dans l'éq. (30a) donne
-
( 33 )
Ceci est la norme équation Fowler-Nordheim type simplifié, en i - V forme. L'équation "physiquement complète" correspondante est obtenue en multipliant par λ Z P F .
Équations modifiées pour les émetteurs à grande surface
Les équations de la section précédente s'appliquent à tous les émetteurs de champ fonctionnant en régime CFE. Cependant, d'autres développements sont utiles pour les émetteurs de grande surface qui contiennent de nombreux sites d'émission individuels.
Pour ces émetteurs, la zone d'émission fictive sera presque toujours très très beaucoup moins que la zone géométrique « macroscopique » apparente ( A M ) de l'émetteur physique observé visuellement. Un paramètre sans dimension de r , l'efficacité de la zone d'émission , peut être définie par
-
( 34 )
Aussi, une densité de courant d'émission « macroscopique » (ou « moyenne ») J M (moyenne sur l'aire géométrique A M de l'émetteur) peut être définie, et rapportée à la densité de courant de référence J r utilisée ci-dessus, par
-
( 35 )
Cela conduit aux "versions à grande surface" suivantes de l'équation standard simplifiée de type Fowler-Nordheim :
-
( 36 )
-
( 37 )
Ces deux équations contiennent l'efficacité de la zone d'émission de la r . Pour un émetteur donné, ce paramètre a une valeur qui n'est généralement pas bien connue. En général, α r varie considérablement entre les différents matériaux émetteurs, et entre les différents échantillons du même matériau préparé et traité de différentes manières. Des valeurs comprises entre 10 -10 et 10 -6 semblent probables, et des valeurs en dehors de cette plage peuvent être possibles.
La présence de α r dans l' équation. (36) explique la différence entre les densités de courant macroscopiques souvent citées dans la littérature (généralement 10 A/m 2 pour de nombreuses formes d'émetteurs à grande surface autres que les réseaux de Spindt ) et les densités de courant locales sur les sites d'émission réels, qui peuvent très variables mais que l'on pense être généralement de l'ordre de 10 9 A/m 2 , voire un peu moins.
Une partie importante de la littérature technique sur les émetteurs de grande surface ne parvient pas à faire une distinction claire entre les densités de courant locales et macroscopiques, ou entre la zone d'émission théorique A r et zone macroscopique A M , et / ou omet le paramètre de r à partir des équations citées. Des précautions sont nécessaires pour éviter les erreurs d'interprétation.
Il est également parfois commode de diviser le facteur de conversion de r dans une « partie macroscopique » qui se rapporte à la géométrie globale de l'émetteur et ses environs, et une « partie locale » qui se rapporte à la capacité de la structure à très locale de la surface de l'émetteur pour améliorer le champ électrique. Cela se fait généralement en définissant un « champ macroscopique » F M qui serait le champ qui serait présent au site émetteur en l'absence de la structure locale qui provoque le rehaussement. Ce champ F M est liée à la tension appliquée par une « tension-champ macroscopique facteur de conversion » β M définie par:
-
( 38 )
Dans le cas courant d'un système comportant deux plaques parallèles, séparées par une distance W , avec des nanostructures émettrices créées sur l'une d'elles, β M = 1/ W .
Un « facteur d'amplification de champ » γ est alors défini et en rapport avec les valeurs de β r et β M par
-
( 39 )
Avec éq. (31), cela génère les formules suivantes :
-
( 40 )
-
( 41 )
où, conformément à la convention habituelle, le suffixe "r" a maintenant été supprimé des paramètres relatifs au point de référence. Il existe des formules pour l'estimation de γ , en utilisant electrostatics classique , pour une variété de formes émetteur, en particulier le « hémisphère sur un poste ».
L'équation (40) implique que des versions des équations de type Fowler-Nordheim peuvent être écrites où F ou βV sont partout remplacés par . Cela se fait souvent dans des applications technologiques où l'intérêt principal est l'amélioration sur le terrain des propriétés de la nanostructure de l'émetteur local. Cependant, dans certains travaux antérieurs, le fait de ne pas faire une distinction claire entre le champ barrière F et le champ macroscopique F M a causé une confusion ou une erreur.
De manière plus générale, les objectifs en matière de développement technologique des émetteurs de champ de grande surface sont d'améliorer l'uniformité des émissions en augmentant la valeur de l'efficacité de la zone d'émission de r et de réduire la tension « apparition » à laquelle se produit l' émission importante, en augmentant la valeur de β . Éq. (41) montre que cela peut se faire de deux façons: soit en essayant de développer « haut gamma nanostructures », ou en modifiant la géométrie globale du système de telle sorte que β M augmente. Divers compromis et contraintes existent.
En pratique, bien que la définition de champ macroscopique utilisée ci-dessus soit la plus courante, d'autres types (définis différemment) de champ macroscopique et de facteur d'amélioration de champ sont utilisés dans la littérature, en particulier en relation avec l'utilisation de sondes pour étudier les caractéristiques i - V des émetteurs individuels.
Dans les contextes technologiques, les données d'émission sur le terrain sont souvent tracées en utilisant (une définition particulière de) F M ou 1/ F M comme coordonnée x . Cependant, pour l'analyse scientifique, il est généralement préférable de ne pas pré-manipuler les données expérimentales, mais de tracer directement les données i - V brutes mesurées . Les valeurs des paramètres technologiques tels que (les différentes formes de) γ peuvent ensuite être obtenues à partir des paramètres ajustés du graphique de données i - V (voir ci-dessous), en utilisant les définitions pertinentes.
Équations modifiées pour les émetteurs nanométriquement pointus
La plupart des dérivations théoriques de la théorie de l'émission de champ sont faites sous l'hypothèse que la barrière prend la forme de Schottky-Nordheim éq. (3). Cependant, cette forme de barrière n'est pas valable pour des émetteurs de rayons de courbure comparables à la longueur de la barrière tunnel. Cette dernière dépend du travail de sortie et du champ, mais dans les cas d'intérêt pratique, l'approximation de la barrière SN peut être considérée comme valable pour les émetteurs de rayons , comme expliqué dans le paragraphe suivant.
L'hypothèse principale de l'approximation de la barrière SN est que le terme de potentiel électrostatique prend la forme linéaire dans la région tunnel. Ce dernier n'a été prouvé que si . Par conséquent, si la région de tunnel a une longueur , pour tout ce qui détermine le processus de tunnel ; donc si éq. (1) est valable et l'approximation de la barrière SN est valide. Si la probabilité d'effet tunnel est suffisamment élevée pour produire une émission de champ mesurable, L ne dépasse pas 1 à 2 nm. Ainsi, la barrière SN est valable pour des émetteurs de rayons de l'ordre de quelques dizaines de nm.
Cependant, les émetteurs modernes sont beaucoup plus pointus que cela, avec des rayons de l'ordre de quelques nm. Par conséquent, l'équation FN standard, ou toute version de celle-ci qui suppose la barrière SN, conduit à des erreurs significatives pour des émetteurs aussi pointus. Cela a été démontré à la fois théoriquement et confirmé expérimentalement.
Le problème ci-dessus a été abordé dans la réf. La barrière SN a été généralisée en tenant compte de la courbure de l'émetteur. Il peut être prouvé que le potentiel électrostatique à proximité de toute surface métallique avec un rayon de courbure peut être asymptotiquement élargi comme
-
( 42 )
De plus, le potentiel image d'un émetteur pointu est mieux représenté par celui correspondant à une surface métallique sphérique plutôt que planaire. Après avoir négligé tous les termes, la barrière potentielle totale prend la forme trouvée par Kyritsakis et Xanthakis
-
( 43 )
Si l' approximation JWKB (4) est utilisée pour cette barrière, l'exposant de Gamow prend une forme qui généralise l'éq. (5)
-
( 44 )
où est défini par (30d), est donné par (30c) et est une nouvelle fonction qui peut être approchée de la même manière que (30c) (il y a des erreurs typographiques dans la référence, corrigées ici) :
-
( 45 )
Étant donné l'expression de l'exposant de Gamow en fonction de la hauteur de barrière sans champ , la densité de courant émis pour l'émission de champ froid peut être obtenue à partir de l'éq. (23). ça donne
-
( 46 )
où les fonctions et sont définies comme
-
( 47a )
et
-
( 47b )
Dans l'équation (46), à des fins d'exhaustivité, n'est pas approximée par l'unité comme dans (29) et (30a), bien que pour la plupart des cas pratiques, il s'agisse d'une très bonne approximation. En dehors de cela, les équations (43), (44) et (46) coïncident avec celles correspondantes de la théorie standard de Fowler-Nordheim (3), (9) et (30a), à la limite ; ceci est attendu puisque les premières équations généralisent les secondes.
Enfin, notez que l'analyse ci-dessus est asymptotique à la limite , de la même manière que la théorie standard de Fowler-Nordheim utilisant la barrière SN. Cependant, l'ajout des termes quadratiques le rend nettement plus précis pour les émetteurs avec des rayons de courbure compris entre ~5 et 20 nm. Pour les émetteurs plus pointus, il n'y a pas d'approximation générale pour la densité de courant. Afin d'obtenir la densité de courant, il faut calculer le potentiel électrostatique et évaluer numériquement l' intégrale JWKB . A cet effet, des bibliothèques de logiciels de calcul scientifique ont été développées.
Equation empirique CFE i – V
Au stade actuel du développement de la théorie CFE, il est important de faire une distinction entre les équations CFE théoriques et une équation CFE empirique. Les premiers sont dérivés de la physique de la matière condensée (bien que dans des contextes où leur développement détaillé est difficile). Une équation empirique CFE, d'autre part, tente simplement de représenter la forme expérimentale réelle de la dépendance du courant i sur la tension V .
Dans les années 1920, des équations empiriques ont été utilisées pour trouver la puissance de V qui apparaissait dans l'exposant d'une équation semi-logarithmique supposée décrire les résultats CFE expérimentaux. En 1928, théorie et expérience ont été réunies pour montrer que (sauf, peut-être, pour les émetteurs très pointus) cette puissance est V -1 . Il a récemment été suggéré que les expériences de CFE doivent maintenant être menées pour essayer de trouver la puissance ( κ ) de V dans la pré-exponentielle de l'équation CFE empirique suivante:
-
( 48 )
où B , C et κ sont traitées comme des constantes.
De l'éq. (42) il est facile de montrer que
-
( 49 )
Dans les années 1920, les techniques expérimentales ne pouvaient pas distinguer les résultats κ = 0 (supposés par Millikan et Laurtisen) et κ = 2 (prédit par l'équation originale de type Fowler-Nordheim). Cependant, il devrait être possible de faire raisonnablement des mesures précises de DLNI / d (1 / V) ( le cas échéant à l'aide d' amplificateur de verrouillage techniques de détection / sensible à la phase et de l' équipement commandé par ordinateur), et pour dériver κ à partir de la pente d'un graphique de données approprié.
Suite à la découverte de l'approximation (30b), il est maintenant très clair que – même pour le CFE à partir de métaux en vrac – la valeur κ =2 n'est pas attendue. Ceci peut être montré comme suit. En utilisant l'éq. (30c) ci-dessus, un paramètre sans dimension η peut être défini par
-
( 50 )
Pour φ = 4,50 eV, ce paramètre a la valeur η = 4,64. Etant donné que f = F / F φ et v ( f ) est donnée par l' équation (30b), l'exposant dans l'équation de Fowler-Nordheim de type standard simplifié (30) peut être écrite sous une autre forme et ensuite développée comme suit:
-
( 51 )
À condition que le facteur de conversion β est indépendant de la tension, le paramètre f a la définition alternative f = V / V φ , où V φ est la tension nécessaire, dans un système expérimental particulier, de réduire la hauteur d'une barrière Schottky-Nordheim à partir de φ à zéro. Ainsi, il est clair que le facteur v ( f ) dans l' exposant de l'équation théorique (30) donne lieu à une dépendance V supplémentaire dans la pré-exponentielle de l'équation empirique. Ainsi, (pour les effets dus à la barrière Schottky-Nordheim, et pour un émetteur avec φ = 4,5 eV) , on obtient la prédiction:
-
( 52 )
Puisqu'il peut également y avoir une dépendance de la tension dans d'autres facteurs dans une équation de type Fowler-Nordheim, en particulier dans la zone d'émission notionnelle A r et dans le travail de sortie local, on ne s'attend pas nécessairement à ce que κ pour CFE d'un métal de la fonction de travail 4,5 eV devrait avoir la valeur κ = 1,23, mais il n'y a certainement aucune raison de s'attendre à ce qu'elle ait la valeur originale de Fowler-Nordheim κ = 2.
Un premier test expérimental de cette proposition a été réalisé par Kirk, qui a utilisé une forme d'analyse de données légèrement plus complexe pour trouver une valeur de 1,36 pour son paramètre κ . Son paramètre κ est très similaire, mais pas tout à fait le même que le paramètre κ utilisé ici, mais néanmoins ses résultats ne semblent confirmer l'utilité potentielle de cette forme d'analyse.
L' utilisation de l'équation empirique de CFE (42), et la mesure de la κ , peut être particulièrement utile pour les non-métaux. Strictement, les équations de type Fowler-Nordheim s'appliquent uniquement à l'émission de la bande de conduction des solides cristallins en vrac . Cependant, les équations empiriques de forme (42) devraient s'appliquer à tous les matériaux (bien que, de manière concevable, une modification puisse être nécessaire pour les émetteurs très pointus). Il semble très probable qu'une manière dont les équations CFE pour les matériaux plus récents peuvent différer des équations de type Fowler-Nordheim est que ces équations CFE peuvent avoir une puissance différente de F (ou V ) dans leurs pré-exponentielles. Les mesures de κ pourraient fournir une indication expérimentale de cela.
Parcelles de Fowler-Nordheim et parcelles de Millikan-Lauritsen
L'équation théorique originale dérivée par Fowler et Nordheim a, au cours des 80 dernières années, influencé la façon dont les données expérimentales CFE ont été tracées et analysées. Dans le diagramme de Fowler-Nordheim très largement utilisé, tel qu'introduit par Stern et al. en 1929, la quantité ln{ i / V 2 } est reportée sur 1/ V . L'idée originale était que (comme prédit par l'équation originale ou élémentaire de type Fowler-Nordheim) cela générerait une droite exacte de pente S FN . S FN serait lié aux paramètres qui apparaissent dans l'exposant d'une équation de type Fowler-Nordheim de forme i - V par :
-
( 47 )
Par conséquent, la connaissance de φ permettrait de déterminer β , ou vice versa.
[En principe, dans des géométries du système où il y a présence d'nanostructure améliorant domaine local, et le facteur de conversion macroscopique β M peut être déterminée, la connaissance de β permet alors la valeur du facteur effectif d'amplification de champ de l'émetteur γ à déterminer à partir de la formule γ = β / β M . Dans le cas courant d'un émetteur à film généré sur une plaque d'un arrangement à deux plaques avec séparation de plaques W (donc β M = 1/ W ) alors
-
( 48 )
De nos jours, c'est l'une des applications les plus probables des parcelles de Fowler-Nordheim.]
Il est ensuite devenu clair que la pensée originale ci-dessus n'est strictement correcte que pour la situation physiquement irréaliste d'un émetteur plat et d'une barrière triangulaire exacte. Pour les émetteurs réels et les obstacles réels un « facteur de correction de pente » σ FN doit être introduit, ce qui donne la formule révisée
-
( 49 )
La valeur de σ FN sera, en principe, être influencé par un paramètre dans l'équation physique complet de type Fowler-Nordheim pour i ( V ) qui a une dépendance à la tension.
À l'heure actuelle, le seul paramètre considéré comme important est le facteur de correction lié à la forme de la barrière, et la seule barrière pour laquelle il existe une théorie détaillée bien établie est la barrière de Schottky-Nordheim. Dans ce cas, σ FN est donné par une fonction mathématique appelée s . Cette fonction s a été calculée pour la première fois correctement (en fonction du paramètre de Nordheim y ) par Burgess, Kroemer et Houston en 1953 ; et un traitement moderne qui donne s en fonction du champ de barrière mis à l'échelle f pour une barrière Schottky-Nordheim est donné. Cependant, il est clair depuis longtemps que, pour le fonctionnement pratique de l'émetteur, la valeur de s est comprise entre 0,9 et 1 .
En pratique, en raison de la complexité supplémentaire liée à la prise en compte détaillée du facteur de correction de pente, de nombreux auteurs placent (en effet) σ FN = 1 dans l'éq. (49), générant de ce fait une erreur systématique dans leurs valeurs estimées de β et / ou γ , généralement considéré comme environ 5%.
Cependant, l' équation empirique (42) - qui est en principe plus général que les équations Fowler-Nordheim de type - apporte avec lui d' éventuelles nouvelles façons d'analyser émission de champ i - V données. En général, on peut supposer que le paramètre B dans l'équation empirique est lié à la hauteur non réduite H d'une barrière caractéristique vue par les électrons tunnel par
-
( 50 )
(Dans la plupart des cas, mais pas nécessairement tous, H serait égal au travail de sortie local ; c'est certainement vrai pour les métaux.) La question est de savoir comment déterminer la valeur de B par l'expérience. Il y a deux manières évidentes. (1) Supposons que l'éq. (43) peut être utilisé pour déterminer une valeur expérimentale raisonnablement précise de κ , de la pente d'une courbe de la forme [-d ln { i } / d (1 / V ) par rapport à V ]. Dans ce cas, une seconde parcelle, de ln ( i ) / V κ par rapport à 1 / V , doit être une ligne droite de pente exacte - B . Cette approche devrait être la façon la plus précise de déterminer B .
(2) En variante, si la valeur de κ est pas exactement connue, et ne peut pas être mesurée avec précision, mais peut être estimée ou deviné, une valeur de B peut être dérivé à partir d' un tracé de la forme [ln { i } par rapport à 1 / V ]. C'est la forme d'intrigue utilisée par Millikan et Lauritsen en 1928. Réorganisation de l'éq. (43) donne
-
( 51 )
Ainsi, B peut être déterminé, à un bon degré d'approximation, en déterminant la pente moyenne d'un tracé de Millikan-Lauritsen sur une certaine plage de valeurs de 1/ V , et en appliquant une correction, en utilisant la valeur de 1/ V à la milieu de la plage et une valeur supposée de κ .
Les principaux avantages de l'utilisation d'un tracé de Millikan-Lauritsen et de cette forme de procédure de correction, plutôt qu'un tracé de Fowler-Nordheim et un facteur de correction de pente, sont les suivants. (1) La procédure de tracé est légèrement plus simple. (2) La correction fait intervenir un paramètre physique ( V ) qui est une grandeur mesurée, plutôt qu'un paramètre physique ( f ) qu'il faut calculer [afin de calculer ensuite une valeur de s ( f ) ou, plus généralement σ FN ( f )]. (3) Le paramètre κ lui-même et la procédure de correction sont plus transparents (et plus faciles à comprendre) que les équivalents du tracé de Fowler-Nordheim. (4) Cette procédure prend en compte tous les effets physiques qui influencent la valeur de κ , alors que la procédure de correction de tracé Fowler-Nordheim (sous la forme dans laquelle il a été réalisé au cours des 50 dernières années) prend en compte que les effets associée à une forme de barrière – en supposant, de plus, que cette forme est celle d'une barrière Schottky-Nordheim. (5) Il y a une séparation plus propre des préoccupations théoriques et technologiques: les théoriciens seront intéressés à établir quelles informations les valeurs mesurées de κ fournissent de la théorie CFE; mais expérimentateurs peuvent simplement utiliser les valeurs mesurées de κ pour faire des estimations plus précises ( le cas échéant) des facteurs d'amélioration sur le terrain.
Cette procédure de correction pour les tracés de Millikan-Lauritsen deviendra plus facile à appliquer lorsqu'un nombre suffisant de mesures de κ aura été effectué et qu'une meilleure idée sera disponible de ce que sont réellement les valeurs typiques. À l'heure actuelle, il semble probable que pour la plupart des matériaux κ se situera dans la plage -1< κ <3.
Plus d'informations théoriques
Développer la théorie approximative du CFE à partir des métaux ci-dessus est relativement facile, pour les raisons suivantes. (1) La théorie des électrons libres de Sommerfeld , avec ses hypothèses particulières sur la distribution des états électroniques internes en énergie, s'applique de manière adéquate à de nombreux métaux en première approximation. (2) La plupart du temps, les métaux n'ont pas d' états de surface et (dans de nombreux cas) les fonctions d'onde des métaux n'ont pas de " résonances de surface " significatives . (3) Les métaux ont une densité élevée d'états au niveau de Fermi, de sorte que la charge qui génère/écrans les champs électriques externes se trouve principalement à l'extérieur de la couche atomique supérieure, et aucune "pénétration de champ" significative ne se produit. (4) Les métaux ont une conductivité électrique élevée : aucune chute de tension significative ne se produit à l'intérieur des émetteurs métalliques : cela signifie qu'il n'y a pas de facteurs obstruant l'apport d'électrons à la surface émettrice, et que les électrons dans cette région peuvent être à la fois en équilibre thermodynamique local effectif et en équilibre thermodynamique effectif avec les électrons dans la structure de support métallique sur laquelle l'émetteur est monté. (5) Les effets au niveau atomique ne sont pas pris en compte.
Le développement de théories "simples" de l'émission d'électrons de champ, et en particulier le développement d'équations de type Fowler-Nordheim, repose sur la véracité des cinq facteurs ci-dessus. Pour les matériaux autres que les métaux (et pour les émetteurs métalliques atomiquement tranchants), un ou plusieurs des facteurs ci-dessus seront faux. Par exemple, les semi - conducteurs cristallins n'ont pas de structure de bande de type électron libre, ont des états de surface, sont sujets à une pénétration de champ et à une courbure de bande , et peuvent présenter à la fois des chutes de tension internes et un découplage statistique de la distribution des électrons de l'état de surface à partir de la distribution des électrons dans la région de surface de la structure de bande massive (ce découplage est connu sous le nom de "l'effet Modinos").
En pratique, la théorie du processus de creusement d'un tunnel de Fowler-Nordheim est à peu près la même pour tous les matériaux (bien que les détails de la forme de la barrière puissent varier, et une théorie modifiée doit être développée pour les états initiaux qui sont localisés plutôt que des ondes progressives. ). Cependant, malgré de telles différences, on s'attend (pour les situations d' équilibre thermodynamique ) à ce que toutes les équations CFE aient des exposants qui se comportent de manière généralement similaire. C'est pourquoi l'application d'équations de type Fowler-Nordheim à des matériaux hors du cadre des dérivations données ici fonctionne souvent. Si l'intérêt porte uniquement sur les paramètres (tels que le facteur d'amélioration du champ) qui se rapportent à la pente des tracés de Fowler-Nordheim ou de Millikan-Lauritsen et à l'exposant de l'équation CFE, alors la théorie de type Fowler-Nordheim donnera souvent des estimations raisonnables. Cependant, les tentatives pour dériver des valeurs de densité de courant significatives échoueront généralement ou toujours.
Notez qu'une ligne droite dans un tracé de Fowler-Nordheim ou de Millikan-Lauritsen n'indique pas que l'émission du matériau correspondant obéit à une équation de type Fowler-Nordheim : elle indique seulement que le mécanisme d'émission pour les électrons individuels est probablement un effet tunnel de Fowler-Nordheim.
Différents matériaux peuvent avoir des distributions d'énergie radicalement différentes de leurs états électroniques internes, de sorte que le processus d'intégration des contributions de densité de courant sur les états électroniques internes peut donner lieu à des expressions significativement différentes pour les pré-exponentielles de densité de courant, pour différentes classes de matériaux . En particulier, la puissance du champ barrière apparaissant dans la pré-exponentielle peut être différente de la valeur originale de Fowler-Nordheim "2". L'étude des effets de ce type est un sujet de recherche actif. Les effets de « résonance » et de « diffusion » au niveau atomique , s'ils se produisent, modifieront également la théorie.
Lorsque les matériaux sont soumis à une pénétration de champ et à une flexion de bande, un préalable nécessaire est d'avoir de bonnes théories de ces effets (pour chaque classe différente de matériau) avant que des théories détaillées de la CFE puissent être développées. Lorsque des effets de chute de tension se produisent, la théorie du courant d'émission peut, dans une plus ou moins grande mesure, devenir une théorie qui implique des effets de transport interne, et peut devenir très complexe.
Voir également
- Microscope à émission de champ
- Sondes à émission de champ
- Réseau d'émetteurs de champ
- Affichage d'émission de champ
- Effet Franz-Keldysh
Les références
Lectures complémentaires
informations générales
- W. Zhu, éd. (2001). Microélectronique sous vide . Wiley, New York.
- GN Fursey (2005). Emission de champ en microélectronique sous vide . Kluwer Academic, New York. ISBN 0-306-47450-6.
Pénétration de champ et flexion de bande (semi-conducteurs)
- Seiwatz, Ruth ; Vert, Mino (1958). "Calculs de charge d'espace pour les semi-conducteurs". Journal de physique appliquée . 29 (7): 1034. bibcode : 1958JAP .... 29.1034S . doi : 10.1063/1.1723358 .
- A. Many, Y. Goldstein et NB Grover, Semiconductor Surfaces (North Holland, Amsterdam, 1965).
- W. Mönsch, Semiconductor Surfaces and Interfaces (Springer, Berlin, 1995).
- Peng, Jie ; Li, Zhibing ; Lui, Chunshan ; Chen, Guihua ; Wang, Weiliang ; Deng, Shaozhi ; Xu, Ningsheng ; Zheng, Xiao; Chen, GuanHua; Edgcombe, Chris J.; Forbes, Richard G. (2008). « Les rôles des dipôles d'apex et de la pénétration du champ dans la physique des nanotubes de carbone à paroi unique chargés, émetteurs de champ ». Journal de physique appliquée . Éditions AIP. 104 (1) : 014310–014310–12. arXiv : cond-mat/0612600 . Bibcode : 2008JAP ... 104a4310P . doi : 10.1063/1.2946449 . ISSN 0021-8979 . S2CID 53453404 .
Charge d'espace sous vide émise par le champ
- Barbour, juge de paix ; Dolan, WW ; Trolan, JK ; Martin, EE ; Dyke, WP (1953). "Effets de charge d'espace dans l'émission de champ". Examen physique . 92 (1) : 45-51. Bibcode : 1953PhRv ... 92 ... 45B . doi : 10.1103/PhysRev.92.45 .
Emission de champ à haute température et émission de champ photo
- Jensen, Kévin (2007). Physique d'émission d'électrons . Avancées dans l'imagerie et la physique des électrons. 149 . San Diego : Presse académique. ISBN 978-0-12-374207-0. OCLC 647688316 .
Émission d'électrons explosive induite par le champ
- GA Mesyats, Explosive Electron Emission (URO Press, Ekaterinbourg, 1998),


![{\displaystyle {\frac {\hbar ^{2}}{2m}}{\frac {\mathrm {d} ^{2}\Psi (x)}{\mathrm {d} x^{2}}} =\gauche[U(x)-E_{\mathrm {n} }\droit]\Psi (x)=M(x)\Psi (x),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7058b8c28ac908f2d76c49148eb63c3776c14db7)















![{\displaystyle D(h,F)\approx P\exp \left[-{\frac {\nu (h,F)bh^{3/2}}{F}}\right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d30f534f18041d34f07faf49fbde58fafb0469a8)

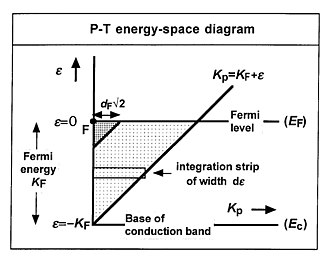



![{\displaystyle \,f_{\mathrm {FD} }(\epsilon )=1/[1+\exp(\epsilon /k_{\mathrm {B} }T)],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/660073ac9b1e45fd059fa35ceefae7ad8231b715)



![{\displaystyle j(\epsilon )\mathrm {d} \epsilon =z_{\mathrm {S} }f_{\mathrm {FD} }\left[\int D\mathrm {d} K_{\mathrm {p} }\right]\mathrm {d} \epsilon =z_{\mathrm {S} }f_{\mathrm {FD} }D_{\mathrm {F} }\exp(\epsilon /d_{\mathrm {F} } )\left[\int _{0}^{\infty }\exp(-K_{\mathrm {p} }/d_{\mathrm {F} })\;\mathrm {d} K_{\mathrm {p } }\right]\mathrm {d} \epsilon ,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8da05680c864fea717f4d0b595de9e68176cc179)



![j_{{{\mathrm {F}}}}[\,=z_{{{\mathrm {S}}}}d_{{{\mathrm {F}}}}D_{{{\mathrm {F}} }}]](https://wikimedia.org/api/rest_v1/media/math/render/svg/de3027bd63c37a2b4cd18c7e5012f8b2b41ada7d)




![Z_{{{\mathrm {F}}}}\;[=z_{{{\mathrm {S}}}}{d_{{{\mathrm {F}}}}}^{2}]](https://wikimedia.org/api/rest_v1/media/math/render/svg/bfb68413338808e05643c49192e35aec75fe3a1b)


![{\displaystyle J=J_{0}\int _{-\infty }^{\infty }{\frac {\exp(\epsilon /d_{\mathrm {F} })}{1+\exp[(\ epsilon /d_{\mathrm {F} })(d_{\mathrm {F} }/k_{\mathrm {B} }T)]}}\mathrm {d} (\epsilon /d_{\mathrm {F} })=\lambda _{T}J_{0},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/10785b91c0dd2ea0d955498481a575bde22d7a25)






![{\displaystyle J\;=\lambda _{Z}a\phi ^{-1}F^{2}P_{\mathrm {F} }\exp[-\nu _{\mathrm {F} }b\ phi ^{3/2}/F],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/900452af376888508ef76737604e223af9e44b0f)

![{\displaystyle J=\;a{\phi ^{-1}}F^{2}\exp[-v(f)\;b\phi ^{3/2}/F],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c4595aa0fd980342356c053a5b6bb79409fb980f)





![{\displaystyle i=\;A_{\mathrm {r} }a{\phi ^{-1}}{\beta }^{2}V^{2}\exp[-v(f)\;b\ phi ^{3/2}/\beta V],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f3a056bb4c941e9fa59328da443f9ae0a40aede0)


![{\displaystyle J_{\mathrm {M} }=\alpha _{\mathrm {r} }a{\phi ^{-1}}F^{2}\exp[-v(f)\;b\phi ^{3/2}/F],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0dc6cc234bb48474d4aa6cc7409dc8336d99a130)
![{\displaystyle i=\;\alpha _{\mathrm {r} }A_{\mathrm {M} }a{\phi ^{-1}}{\beta }^{2}V^{2}\exp [-v(f)\;b\phi ^{3/2}/\beta V],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/49bd575e7625f9c30236416f06fef2bffa50d3e0)













![{\displaystyle \Phi (x)=Fx\left[1-{\frac {x}{R}}+O\left({\frac {x}{R}}\right)^{2}\right] {\text{, pour }}x\ll R.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/660a832825987696fe625e26a8c96436e390d725)








![{\displaystyle J=a{\frac {F^{2}}{\phi }}\left({\frac {1}{\lambda _{d}(f)}}+{\frac {\phi } {eFR}}\psi (f)\right)^{-2}\exp \left[-{\frac {b\phi ^{3/2}}{F}}\left(v(f)+\ oméga (f){\frac {\phi }{eFR}}\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a0ac43807880de73c5230d12b7ea0812d6c26d9c)






![{\displaystyle i=\;CV^{\kappa }\exp[-B/V],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/35935a7f777a488f830fc6fdff558b38f5a61e3d)


![{\displaystyle \exp[-v(f)\;b{\phi }^{3/2}/F]\;=\;\exp[-v(f)\;\eta /f]\;\ approx \;{\mathrm {e} }^{\eta }f^{-\eta /6}\exp[-\eta /f]\;=\;{\mathrm {e} }^{\eta } f^{-\eta /6}\exp[-b{\phi }^{3/2}/F].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5432c37c43c2816b5d69d8c1acfd99d38c03aec4)






