Numéro surréaliste - Surreal number

En mathématiques , le système de nombres surréalistes est une classe propre totalement ordonnée contenant les nombres réels ainsi que des nombres infinis et infinitésimaux , respectivement plus grands ou plus petits en valeur absolue que tout nombre réel positif. Les surréalistes partagent de nombreuses propriétés avec les réels, y compris les opérations arithmétiques habituelles (addition, soustraction, multiplication et division) ; en tant que tels, ils forment un champ ordonné . S'ils sont formulés dans la théorie des ensembles de von Neumann-Bernays-Gödel , les nombres surréalistes sont un champ ordonné universel au sens où tous les autres champs ordonnés, tels que les rationnels, les réels, les fonctions rationnelles , le champ de Levi-Civita , les nombres surréels , et les nombres hyperréels , peuvent être réalisés comme des sous-champs des surréalistes. Les surréalistes contiennent aussi tous les nombres ordinaux transfinis ; l'arithmétique sur eux est donnée par les opérations naturelles . Il a également été montré (dans la théorie des ensembles de von Neumann-Bernays-Gödel) que le champ hyperréal de classe maximale est isomorphe au champ surréaliste de classe maximale.

Histoire du concept

Les recherches sur la phase finale de Go par John Horton Conway ont conduit à la définition et à la construction originales des nombres surréalistes. La construction de Conway a été introduite dans le livre de 1974 de Donald Knuth , Surreal Numbers: How Two Ex-Students Turned On to Pure Mathematics and Found Total Happiness . Dans son livre, qui prend la forme d'un dialogue, Knuth a inventé le terme nombres surréalistes pour ce que Conway avait appelé simplement nombres . Conway a ensuite adopté le terme de Knuth et a utilisé des surréalistes pour analyser les jeux dans son livre de 1976 sur les nombres et les jeux .

Une voie distincte pour définir les surréalistes a commencé en 1907, lorsque Hans Hahn a présenté les séries de Hahn comme une généralisation des séries de puissance formelles , et Hausdorff a introduit certains ensembles ordonnés appelés η _α -ensembles pour les ordinaux α et a demandé s'il était possible de trouver un ensemble ordonné compatible. structure de groupe ou de terrain. En 1962, Alling a utilisé une forme modifiée de série de Hahn pour construire de tels champs ordonnés associés à certains ordinaux , et en 1987 il a montré que prendre pour être la classe de tous les ordinaux dans sa construction donne une classe qui est un champ ordonné isomorphe au nombres surréalistes.

Si les surréalistes sont considérés comme « juste » un champ réel fermé de la taille d'une classe appropriée, l'article d'Alling de 1962 traite le cas des cardinaux fortement inaccessibles qui peuvent naturellement être considérés comme des classes appropriées en coupant la hiérarchie cumulative de l'univers un étage au-dessus du cardinal, et Alling mérite donc beaucoup de crédit pour la découverte/invention des surréalistes dans ce sens. Il y a une structure de champ supplémentaire importante sur les surréalistes qui n'est pas visible à travers cette lentille cependant, à savoir la notion d'"anniversaire" et la description naturelle correspondante des surréalistes comme résultat d'un processus de remplissage le long de leurs anniversaires donné par Conway. Cette structure supplémentaire est devenue fondamentale pour une compréhension moderne des nombres surréalistes, et Conway se voit ainsi attribuer le mérite d'avoir découvert les surréalistes tels que nous les connaissons aujourd'hui.

Aperçu

Dans la construction Conway, les nombres surréels sont construits en plusieurs étapes, avec un ordre ≤ telle que pour deux nombres surréels a et b , a ≤ b ou b ≤ a . (Les deux peuvent être vérifiés, auquel cas a et b sont équivalents et désignent le même nombre.) Chaque nombre est formé d'une paire ordonnée de sous-ensembles de nombres déjà construits : des sous-ensembles donnés L et R de nombres tels que tous les membres de L sont strictement inférieur à tous les membres de R , alors le couple { L | R } représente un nombre intermédiaire en valeur entre tous les membres de L et tous les membres de R .

Différents sous-ensembles peuvent finir par définir le même nombre : { L | R } et { L′ | R ' } peut définir le même nombre , même si L ≠ L' et R ≠ R ' . (Un phénomène similaire se produit lorsque les nombres rationnels sont définis comme des quotients d'entiers : 1/2 et 2/4 sont des représentations différentes du même nombre rationnel.) Donc à proprement parler, les nombres surréalistes sont des classes d'équivalence de représentations de la forme { L | R } qui désignent le même nombre.

Dans la première étape de la construction, il n'y a pas de nombres existants, la seule représentation doit donc utiliser l'ensemble vide : { | } . Cette représentation, où L et R sont tous deux vides, est appelée 0. Les étapes suivantes donnent des formes comme

{ 0 | } = 1

{ 1 | } = 2

{ 2 | } = 3

et

{ | 0 } = -1

{ | -1 } = -2

{ | -2 } = -3

Les nombres entiers sont donc contenus dans les nombres surréalistes. (Les identités ci-dessus sont des définitions, dans le sens où le côté droit est un nom pour le côté gauche. Que les noms soient réellement appropriés sera évident lorsque les opérations arithmétiques sur les nombres surréalistes seront définies, comme dans la section ci-dessous ). De même, des représentations telles que

{ 0 | 1 } = 1/2

{ 0 | 1/2} = 1/4

{ 1/2 | 1 } = 3/4

surviennent, de sorte que les rationnels dyadiques (nombres rationnels dont les dénominateurs sont des puissances de 2) sont contenus dans les nombres surréalistes.

Après un nombre infini d'étapes, des sous-ensembles infinis deviennent disponibles, de sorte que tout nombre réel a peut être représenté par { L _a | R _a }, où L _a est l'ensemble de tous les rationnels dyadiques inférieurs à a et R _a est l'ensemble de tous les rationnels dyadiques supérieurs à a (rappelant une coupe de Dedekind ). Ainsi, les nombres réels sont également intégrés dans les surréalistes.

Il y a aussi des représentations comme

{ 0, 1, 2, 3, ... | } = ω

{ 0 | 1, 1/2, 1/4, 1/8, ... } =

où ω est un nombre transfini supérieur à tous les entiers et ε est un nombre infinitésimal supérieur à 0 mais inférieur à tout nombre réel positif. De plus, les opérations arithmétiques standard (addition, soustraction, multiplication et division) peuvent être étendues à ces nombres non réels d'une manière qui transforme la collection de nombres surréalistes en un champ ordonné, de sorte que l'on peut parler de 2ω ou ω − 1 et ainsi de suite.

Construction

Les nombres surréalistes sont construits inductivement en tant que classes d'équivalence de paires d'ensembles de nombres surréalistes, limités par la condition que chaque élément du premier ensemble soit plus petit que chaque élément du second ensemble. La construction se compose de trois parties interdépendantes : la règle de construction, la règle de comparaison et la règle d'équivalence.

Formes

Une forme est une paire d'ensembles de nombres surréalistes, appelés son ensemble de gauche et son ensemble de droite . Une forme avec l'ensemble gauche L et l'ensemble droit R s'écrit { L | R } . Lorsque L et R sont donnés sous forme de listes d'éléments, les accolades qui les entourent sont omises.

L'un ou les deux ensembles gauche et droit d'un formulaire peuvent être l'ensemble vide. La forme { { } | { } } avec les deux ensembles gauche et droit vides est également écrit { | } .

Formes numériques et leurs classes d'équivalence

Règle de construction

Un formulaire { L | R } est numérique si l'intersection de L et R est l'ensemble vide et que chaque élément de R est supérieur à chaque élément de L , selon la relation d'ordre ≤ donnée par la règle de comparaison ci-dessous.

Les formes numériques sont placées dans des classes d'équivalence ; chacune de ces classes d'équivalence est un nombre surréaliste . Les éléments de l'ensemble gauche et droit d'une forme sont tirés de l'univers des nombres surréalistes (non pas des formes , mais de leurs classes d'équivalence ).

Règle d'équivalence

Deux formes numériques x et y sont des formes du même nombre (appartenant à la même classe d'équivalence) si et seulement si à la fois x ≤ y et y ≤ x .

Une relation d'ordre doit être antisymétrique , c'est-à-dire qu'elle doit avoir la propriété que x = y (c'est-à-dire que x ≤ y et y ≤ x sont tous les deux vrais) uniquement lorsque x et y sont le même objet. Ce n'est pas le cas pour les formes de nombres surréalistes , mais c'est vrai par construction pour les nombres surréalistes (classes d'équivalence).

La classe d'équivalence contenant { | } est étiqueté 0 ; en d'autres termes, { | } est une forme du nombre surréaliste 0.

Commander

La définition récursive des nombres surréalistes est complétée par la définition de la comparaison :

Étant donné les formes numériques x = { X _L | X _R } et y = { Y _L | Y _R }, x ≤ y si et seulement si :

• Il n'y a pas x _L ∈ X _L de telle sorte que y ≤ x _L (tous les éléments dans la partie gauche de x est inférieur à y ), et
• Il n'y a pas y _R ∈ Y _R tel que y _R ≤ x (chaque élément dans la partie droite de y est supérieur à x ).

Une comparaison y ≤ c entre une forme y et un nombre surréaliste c est effectuée en choisissant une forme z de la classe d'équivalence c et en évaluant y ≤ z ; et de même pour c ≤ x et pour la comparaison b ≤ c entre deux nombres surréalistes.

Induction

Ce groupe de définitions est récursif et nécessite une certaine forme d' induction mathématique pour définir l'univers des objets (formes et nombres) qui s'y trouvent. Les seuls nombres surréalistes accessibles par induction finie sont les fractions dyadiques ; un univers plus large est accessible étant donné une certaine forme d' induction transfinie .

Règle d'induction

• Il existe une génération S ₀ = { 0 }, dans laquelle 0 se compose de la forme unique { | }.
• Étant donné un nombre ordinal n , la génération S _n est l'ensemble de tous les nombres surréalistes générés par la règle de construction à partir de sous-ensembles de .${\displaystyle \cup _{i<n}S_{i}}$

Le cas de base est en fait un cas particulier de la règle d'induction, avec 0 pris comme étiquette pour le "plus petit ordinal". Puisqu'il n'existe pas de S _i avec i < 0, l'expression est l'ensemble vide ; le seul sous-ensemble de l'ensemble vide est l'ensemble vide, et donc S ₀ consiste en une seule forme surréaliste { | } se trouvant dans une seule classe d'équivalence 0. ${\displaystyle \cup _{i<0}S_{i}}$

Pour tout nombre ordinal fini n , S _n est bien ordonné par l'ordre induit par la règle de comparaison sur les nombres surréalistes.

La première itération de la règle d'induction produit les trois formes numériques { | 0 } < { | } < { 0 | } (la forme { 0 | 0 } n'est pas numérique car 0≤0). La classe d'équivalence contenant { 0 | } est étiqueté 1 et la classe d'équivalence contenant { | 0 } est étiqueté -1. Ces trois étiquettes ont une signification particulière dans les axiomes qui définissent un anneau ; ce sont l'identité additive (0), l'identité multiplicative (1) et l'inverse additif de 1 (−1). Les opérations arithmétiques définies ci-dessous sont cohérentes avec ces étiquettes.

Pour tout i < n , puisque toute forme valide dans S _i est aussi une forme valide dans S _n , tous les nombres dans S _i apparaissent également dans S _n (en tant que sur-ensembles de leur représentation dans S _i ). (L'expression d'union d'ensemble apparaît dans notre règle de construction, plutôt que la forme plus simple S _{n -1} , de sorte que la définition a également un sens lorsque n est un ordinal limite .) Nombres dans S _n qui sont un sur-ensemble d'un certain nombre dans S _i sont dits avoir été hérités de la génération i . La plus petite valeur de α pour laquelle un nombre surréaliste donné apparaît dans S _α est appelé son anniversaire . Par exemple, l'anniversaire de 0 est 0 et l'anniversaire de -1 est 1.

Une deuxième itération de la règle de construction donne l'ordre suivant des classes d'équivalence :

{ | -1 } = { | -1, 0 } = { | -1, 1 } = { | -1, 0, 1 }

< { | 0 } = { | 0, 1 }

< { -1 | 0 } = { -1 | 0, 1 }

< { | } = { -1 | } = { | 1 } = { -1 | 1 }

< { 0 | 1 } = { -1, 0 | 1 }

< { 0 | } = { -1, 0 | }

< { 1 | } = { 0, 1 | } = { -1, 1 | } = { -1, 0, 1 | }

La comparaison de ces classes d'équivalence est cohérente, quel que soit le choix de la forme. Trois constats s'ensuivent :

1. S ₂ contient quatre nouveaux nombres surréalistes. Deux contiennent des formes extrêmes : { | −1, 0, 1 } contient tous les nombres des générations précédentes dans son ensemble de droite, et { −1, 0, 1 | } contient tous les nombres des générations précédentes dans son ensemble de gauche. Les autres ont une forme qui divise tous les nombres des générations précédentes en deux ensembles non vides.
2. Chaque nombre surréaliste x qui existait dans la "génération" précédente existe également dans cette génération, et comprend au moins une nouvelle forme : une partition de tous les nombres autres que x des générations précédentes en un ensemble de gauche (tous les nombres inférieurs à x ) et un ensemble à droite (tous les nombres supérieurs à x ).
3. La classe d'équivalence d'un nombre ne dépend que de l'élément maximal de son ensemble de gauche et de l'élément minimal de l'ensemble de droite.

Les interprétations informelles de { 1 | } et { | -1 } sont respectivement "le nombre juste après 1" et "le nombre juste avant -1" ; leurs classes d'équivalence sont étiquetées 2 et -2. Les interprétations informelles de { 0 | 1 } et { -1 | 0 } sont respectivement "le nombre à mi-chemin entre 0 et 1" et "le nombre à mi-chemin entre -1 et 0" ; leurs classes d'équivalence sont notées ¹ / ₂ et − ¹ / ₂ . Ces étiquettes seront également justifiées par les règles d'addition et de multiplication surréalistes ci-dessous.

Les classes d'équivalence à chaque étape n de l'induction peuvent être caractérisées par leurs n - formes complètes (chacune contenant autant d'éléments que possible des générations précédentes dans ses ensembles gauche et droit). Soit ce formulaire complet contient tous les nombres des générations précédentes dans son ensemble gauche ou droit, auquel cas c'est la première génération dans laquelle ce nombre apparaît ; ou il contient tous les nombres des générations précédentes sauf un, auquel cas il s'agit d'une nouvelle forme de ce nombre. Nous conservons les étiquettes de la génération précédente pour ces "anciens" numéros, et écrivons l'ordre ci-dessus en utilisant les anciennes et les nouvelles étiquettes :

−2 < −1 < − ¹ / ₂ < 0 < ¹ / ₂ < 1 < 2.

La troisième observation s'étend à tous les nombres surréalistes avec des ensembles finis à gauche et à droite. (Pour les ensembles infinis à gauche ou à droite, ceci est valide sous une forme modifiée, car les ensembles infinis peuvent ne pas contenir d'élément maximal ou minimal.) Le nombre { 1, 2 | 5, 8 } est donc équivalent à { 2 | 5} ; on peut établir qu'il s'agit de formes de 3 en utilisant la propriété birthday , qui est une conséquence des règles ci-dessus.

Propriété d'anniversaire

Une forme x = { L | R } apparaissant dans la génération n représente un nombre hérité d'une génération précédente i < n si et seulement s'il y a un certain nombre dans S _i qui est supérieur à tous les éléments de L et inférieur à tous les éléments de R . (En d'autres termes, si L et R sont déjà séparés par un nombre créé à un stade antérieur, alors x ne représente pas un nouveau nombre mais un déjà construit.) Si x représente un nombre de toute génération antérieure à n , il existe un nombre moins une telle génération i , et exactement un nombre c avec ce moins i comme anniversaire se situe entre L et R ; x est une forme de ce c . En d'autres termes, il appartient à la classe d'équivalence dans S _n qui est un sur-ensemble de la représentation de c dans la génération i .

Arithmétique

L'addition, la négation (inverse additif) et la multiplication de nombres surréalistes forment x = { X _L | X _R } et y = { Y _L | Y _R } sont définis par trois formules récursives.

Négation

Négation d'un nombre donné x = { X _L | X _R } est défini par

${\displaystyle -x=-\{X_{L}|X_{R}\}=\{-X_{R}|-X_{L}\}}$,

où la négation d'un ensemble S de nombres est donnée par l'ensemble des éléments niés de S :

${\displaystyle -S=\{-s:s\in S\}}$.

Cette formule implique la négation des nombres surréalistes apparaissant dans les ensembles gauche et droit de x , ce qui doit être compris comme le résultat du choix d'une forme du nombre, de l'évaluation de la négation de cette forme et de la classe d'équivalence du résultat former. Cela n'a de sens que si le résultat est le même, quel que soit le choix de la forme de l'opérande. Cela peut être prouvé inductivement en utilisant le fait que les nombres apparaissant dans X _L et X _R sont tirés de générations antérieures à celle dans laquelle la forme x apparaît pour la première fois, et en observant le cas particulier :

${\displaystyle -0=-\{|\}=\{|\}=0}$.

Une addition

La définition de l'addition est aussi une formule récursive :

${\displaystyle x+y=\{X_{L}|X_{R}\}+\{Y_{L}|Y_{R}\}=\{X_{L}+y,x+Y_{L} |X_{R}+y,x+Y_{R}\}}$,

où

${\displaystyle X+y=\{x+y:x\in X\},x+Y=\{x+y:y\in Y\}}$.

Cette formule implique des sommes d'un des opérandes originaux et un nombre surréaliste tiré de l'ensemble gauche ou droit de l'autre. Ceux-ci doivent être compris comme le résultat du choix d'une forme de l'opérande numérique, de la somme des deux formes et de la classe d'équivalence de la forme résultante. Cela n'a de sens que si le résultat est le même, quel que soit le choix de forme de l'opérande numérique. Ceci peut également être prouvé inductivement avec les cas particuliers :

0 + 0 = { | } + { | } = { | } = 0

x + 0 = x + { | } = { X _L + 0 | X _R + 0 } = { X _L | X _R } = x

0 + y = { | } + y = { 0 + Y _L | 0 + Y _R } = { Y _L | Y _R } = y

Les deux derniers cas sont eux-mêmes prouvés par induction.

Multiplication

La formule récursive de multiplication contient des expressions arithmétiques impliquant les opérandes et leurs ensembles gauche et droit, comme l'expression qui apparaît dans l'ensemble gauche du produit de x et y . Cela doit être compris comme l'ensemble des nombres surréalistes résultant du choix d'un nombre dans chaque ensemble qui apparaît dans l'expression et de l'évaluation de l'expression sur ces nombres. (Dans chaque évaluation individuelle de l'expression, un seul nombre est choisi dans chaque ensemble et est substitué à chaque endroit où cet ensemble apparaît dans l'expression.) ${\style d'affichage X_{R}y+xY_{R}-X_{R}Y_{R}}$

Cela dépend, à son tour, de la capacité à (a) multiplier des paires de nombres surréalistes tirés des ensembles gauche et droit de x et y pour obtenir un nombre surréaliste, et annuler le résultat ; (b) multiplier la forme de nombre surréaliste x ou y et un nombre surréaliste tiré de l'ensemble gauche ou droit de l'autre opérande pour obtenir un nombre surréaliste ; et (c) additionner les nombres surréalistes résultants. Cela implique à nouveau des cas particuliers, contenant cette fois 0 = { | }, l'identité multiplicative 1 = { 0 | }, et son inverse additif -1 = { | 0}.

${\displaystyle {\begin{aligned}xy&=\{X_{L}|X_{R}\}\{Y_{L}|Y_{R}\}\\&=\left\{X_{L}y +xY_{L}-X_{L}Y_{L},X_{R}y+xY_{R}-X_{R}Y_{R}|X_{L}y+xY_{R}-X_{L} Y_{R},xY_{L}+X_{R}y-X_{R}Y_{L}\right\}\\\end{aligned}}}$

Division

La définition de la division se fait en termes de réciproque et de multiplication :

${\displaystyle {\frac {x}{y}}=x\left({\frac {1}{y}}\right)}$

où

${\displaystyle {\frac {1}{y}}={\Bigg \{}0,{\frac {1+(y_{R}-y)({\frac {1}{y}})_{ L}}{y_{R}}},{\frac {1+(y_{L}-y)({\frac {1}{y}})_{R}}{y_{L}}}{ \Bigg |}{\frac {1+(y_{L}-y)({\frac {1}{y}})_{L}}{y_{L}}},{\frac {1+( y_{R}-y)({\frac {1}{y}})_{R}}{y_{R}}}{\Bigg \}}}$

pour positif . Seuls les positifs sont autorisés dans la formule, tous les termes non positifs étant ignorés (et sont toujours positifs). Cette formule implique non seulement la récursivité en termes de pouvoir diviser par des nombres à partir des ensembles gauche et droit de , mais également la récursivité en ce que les membres des ensembles gauche et droit de lui - même. est toujours un membre de l'ensemble de gauche de , et cela peut être utilisé pour trouver plus de termes de manière récursive. Par exemple, si , alors nous savons qu'un terme gauche de sera . Cela signifie à son tour est un terme juste. Cela signifie est un terme de gauche. Ce moyen sera un terme juste. En continuant, cela donne . ${\textstyle y}$${\textstyle y_{L}}$${\textstyle y_{R}}$${\textstyle y}$${\textstyle {\frac {1}{y}}}$${\styletexte 0}$${\textstyle {\frac {1}{y}}}$${\textstyle y=3=\{2|\}}$${\textstyle {\frac {1}{3}}}$${\styletexte 0}$${\textstyle {\frac {1+(2-3)0}{2}}=1/2}$${\textstyle {\frac {1+(2-3)\left({\frac {1}{2}}\right)}{2}}={\frac {1}{4}}}$${\textstyle {\frac {1+(2-3)\left({\frac {1}{4}}\right)}{2}}={\frac {3}{8}}}$${\textstyle {\frac {1}{3}}=\{0,{\frac {1}{4}},{\frac {5}{16}},\ldots |{\frac {1}{ 2}},{\frac {3}{8}},\ldots \}}$

Pour négatif , est donné par . Si , alors n'est pas défini. ${\textstyle y}$${\textstyle {\frac {1}{y}}}$${\textstyle {\frac {1}{y}}=-\left({\frac {1}{-y}}\right)}$${\style d'affichage y=0}$${\displaystyle {\frac {1}{y}}}$

Cohérence

On peut montrer que les définitions de négation, d'addition et de multiplication sont cohérentes, en ce sens que :

• L'addition et la négation sont définies récursivement en termes d'étapes d'addition et de négation « plus simples », de sorte que les opérations sur les nombres de date de naissance n seront finalement entièrement exprimées en termes d'opérations sur les nombres de date de naissance inférieure à n ;
• La multiplication est définie de manière récursive en termes d'additions, de négations et d'étapes de multiplication "plus simples", de sorte que le produit de nombres avec anniversaire n sera finalement exprimé entièrement en termes de sommes et de différences de produits de nombres avec anniversaires inférieurs à n ;
• Tant que les opérandes sont des formes de nombres surréalistes bien définies (chaque élément de l'ensemble de gauche est inférieur à chaque élément de l'ensemble de droite), les résultats sont à nouveau des formes de nombres surréalistes bien définies ;
• Les opérations peuvent être étendues aux nombres (classes d'équivalence de formes) : le résultat de la négation de x ou de l'addition ou de la multiplication de x et y représentera le même nombre quel que soit le choix de forme de x et y ; et
• Ces opérations obéissent aux axiomes d'associativité, de commutativité, d'inverse additif et de distributivité dans la définition d'un corps , d'identité additive 0 = { | } et identité multiplicative 1 = { 0 | }.

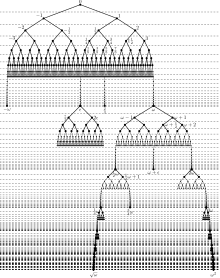
Avec ces règles, on peut maintenant vérifier que les nombres trouvés dans les premières générations ont été correctement étiquetés. La règle de construction est répétée pour obtenir plus de générations de surréalistes :

S ₀ = { 0 }

S ₁ = { -1 < 0 < 1 }

S ₂ = { −2 < −1 < − ¹ / ₂ < 0 < ¹ / ₂ < 1 < 2}

S ₃ = { −3 < −2 < − ³ / ₂ < −1 < − ³ / ₄ < − ¹ / ₂ < − ¹ / ₄ < 0 < ¹ / ₄ < ¹ / ₂ < ³ / ₄ < 1 < ³ / ₂ < 2 < 3 }

S ₄ = { -4 < -3 < ... < − ¹ / ₈ < 0 < ¹ / ₈ < ¹ / ₄ < ³ / ₈ < ¹ / ₂ < ⁵ / ₈ < ³ / ₄ < ⁷ / ₈ < 1 < ⁵ / ₄ < ³ / ₂ < ⁷ / ₄ < 2 < ⁵ / ₂ < 3 < 4 }

Fermeture arithmétique

Pour chaque nombre naturel (ordinal fini) n , tous les nombres générés dans S _n sont des fractions dyadiques , c'est-à-dire qu'ils peuvent être écrits comme une fraction irréductible où a et b sont des nombres entiers et 0 ≤ b < n . ${\displaystyle {\frac {a}{2^{b}}}}$

L'ensemble de tous les nombres surréalistes générés dans certains S _n pour n fini peut être noté S _* = . On peut former les trois classes S ₀ = { 0 }, S ₊ = , et S ₋ = , dont S _* est l'union. Aucun individu S _n n'est fermé par addition et multiplication (sauf S ₀ ), mais S _{* l'} est ; c'est le sous-anneau des rationnels constitué de toutes les fractions dyadiques. ${\displaystyle \cup _{n\in N}S_{n}}$${\displaystyle \{x\in S_{*}:x>0\}}$${\displaystyle \{x\in S_{*}:x<0\}}$

Il existe une infinité de nombres ordinaux pour lesquels l'ensemble des nombres surréalistes dont l'anniversaire est inférieur à est fermé sous les différentes opérations arithmétiques. Pour tout ordinal α, l'ensemble des nombres surréalistes dont la date de naissance est inférieure à β = ω ^α (en utilisant les puissances de ω ) est fermé par addition et forme un groupe ; pour anniversaire inférieur à ω ^{ω α} il est fermé par multiplication et forme un anneau; et pour anniversaire inférieur à un nombre epsilon (ordinal) ε _α il est fermé par inverse multiplicatif et forme un champ. Ces derniers ensembles sont également fermés sous la fonction exponentielle telle que définie par Kruskal et Gonshor.

Cependant, il est toujours possible de construire un nombre surréaliste supérieur à n'importe quel membre d'un ensemble de surréalistes (en incluant l'ensemble sur le côté gauche du constructeur) et donc la collection de nombres surréalistes est une classe appropriée . Avec leur ordre et leurs opérations algébriques, ils constituent un champ ordonné , avec la mise en garde qu'ils ne forment pas un ensemble . En fait, c'est un champ ordonné très spécial : le plus grand. Tout autre champ ordonné peut être intégré dans les surréalistes. La classe de tous les nombres surréalistes est désignée par le symbole . ${\displaystyle \mathbf {Non} }$

Infini

Définir S _ω comme étant l'ensemble de tous les nombres surréels générés par la règle de construction de sous - ensembles de S _* . (C'est la même étape inductive qu'auparavant, puisque le nombre ordinal est le plus petit ordinal qui est plus grand que tous les nombres naturels ; cependant, l'union d'ensembles apparaissant dans l'étape inductive est maintenant une union infinie d'ensembles finis, et donc cette étape ne peut être réalisée que dans une théorie des ensembles qui permet une telle union.) Un unique nombre positif infiniment grand apparaît dans S _ω :

${\displaystyle \omega =\{S_{*}|\}=\{1,2,3,4,...|\}.}$

S _w contient également des objets qui peuvent être identifiés comme les nombres rationnels . Par exemple, la forme ω-complète de la fraction ^une / _trois est donnée par:

${\displaystyle {\tfrac {1}{3}}=\{y\in S_{*}:3y<1|y\in S_{*}:3y>1\}}$.

Le produit de cette forme de ¹ / ₃ avec toute forme de trois est une forme dont l' ensemble de gauche contient uniquement des chiffres inférieur à 1 et dont l' ensemble de droite ne contient que des nombres supérieurs à 1; la propriété d'anniversaire implique que ce produit est une forme de 1.

Non seulement tous les autres nombres rationnels apparaissent dans S _ω ; les nombres réels finis restants aussi. Par exemple,

${\displaystyle \pi =\{3,{\frac {25}{8}},{\frac {201}{64}},...|4,{\frac {7}{2}},{ \frac {13}{4}},{\frac {51}{16}},...\}}$.

Les seuls infinis en S _ω sont ω et -ω; mais il y a d' autres chiffres non réels en S _ω parmi les nombres réels. Tenez compte le plus petit nombre positif S _ω :

${\displaystyle \varepsilon =\{S_{-}\cup S_{0}|S_{+}\}=\{0|1,{\tfrac {1}{2}},{\tfrac {1}{ 4}},{\tfrac {1}{8}},...\}=\{0|y\in S_{*}:y>0\}}$.

Ce nombre est supérieur à zéro mais inférieur à toutes les fractions dyadiques positives. C'est donc un nombre infinitésimal , souvent noté . La forme -complète de ε (respectivement -ε) est la même que la forme ω-complète de 0, sauf que 0 est inclus dans l'ensemble de gauche (respectivement de droite). Les seuls « purs » infinitesimals en S _ω sont ε et -ε son additif inverse; les ajouter à n'importe quelle fraction dyadique y produit les nombres y ±ε, qui se trouvent également dans S _ω .

On peut déterminer la relation entre ω et en en multipliant des formes particulières pour obtenir :

· ε = { · S ₊ | · S ₊ + S _* + · S _* }.

Cette expression n'est bien définie que dans une théorie des ensembles qui permet l'induction transfinie jusqu'à . Dans un tel système, on peut démontrer que tous les éléments de l'ensemble de gauche de ω · sont des infinitésimaux positifs et que tous les éléments de l'ensemble de droite sont des infinités positives, et donc ω · ε est le plus ancien nombre fini positif, c'est-à-dire 1 . Par conséquent, ${\displaystyle S_{\omega ^{2}}}$

¹ / _ε = ω.

Certains auteurs utilisent systématiquement ω ⁻¹ à la place du symbole ε.

Contenu de S _ω

Étant donné x = { L | R } dans S _ω , exactement l'une des conditions suivantes est vraie :

• L et R sont tous les deux vides, auquel cas x = 0 ;
• R est vide et un entier n ≥0 est supérieur à chaque élément de L , auquel cas x est égal au plus petit de ces entiers n ;
• R est vide et aucun entier n n'est supérieur à chaque élément de L , auquel cas x est égal à +ω ;
• L est vide et un entier n ≤0 est inférieur à chaque élément de R , auquel cas x est égal au plus grand de ces entiers n ;
• L est vide et aucun entier n n'est inférieur à chaque élément de R , auquel cas x est égal à -ω ;
• L et R sont tous deux non vides, et :
  • Une fraction dyadique y est « strictement entre » L et R (supérieure à tous les éléments de L et inférieure à tous les éléments de R ), auquel cas x est égal à la plus ancienne fraction dyadique y ;
  • Aucune fraction dyadique y n'est strictement comprise entre L et R , mais une fraction dyadique est supérieure ou égale à tous les éléments de L et inférieure à tous les éléments de R , auquel cas x est égal à y +ε ;${\displaystyle y\in L}$
  • Aucune fraction dyadique y n'est strictement comprise entre L et R , mais une fraction dyadique est supérieure à tous les éléments de L et inférieure ou égale à tous les éléments de R , auquel cas x est égal à y -ε ;${\displaystyle y\in R}$
  • Chaque fraction dyadique est soit supérieure à un élément de R, soit inférieure à un élément de L , auquel cas x est un nombre réel qui n'a pas de représentation en tant que fraction dyadique.

S _ω est pas un champ algébrique, car il n'a pas été fermée par des opérations arithmétiques; considérons ω+1, dont la forme ne se trouve dans aucun nombre de S _ω . Le sous - ensemble maximal de S _ω qui est fermé sous (série finie de) des opérations arithmétiques est le champ de nombres réels, obtenus en laissant de côté les infinis de l'ω, l'ε de infinitésimales, et les voisins de infinitésimales y ± e de chaque valeur non nulle fraction dyadique oui . ${\displaystyle \{1,2,3,4,...|\}+\{0|\}=\{1,2,3,4,...,\omega |\}}$

Cette construction des nombres réels diffère des coupes Dedekind d' analyse standard en ce qu'elle commence à partir de fractions dyadiques plutôt que rationals général et identifie naturellement chaque fraction dyadique en S _ω avec ses formes dans les générations précédentes. (Les formes de co-complet d'éléments réels de S _ω sont dans une correspondance univoque avec les réels obtenus par des coupes de Dedekind, sous réserve que Dedekind réels correspondant aux nombres rationnels sont représentés par la forme dans laquelle le point de coupure est omis des ensembles gauche et droit.) Les rationnels ne sont pas une étape identifiable dans la construction surréaliste ; elles ne sont que le sous - ensemble Q de S _ω contenant tous les éléments x tels que x b = un pour certains un et certains non nul b , tous deux établis à partir de S _* . En démontrant que Q est clos sous des répétitions individuelles des opérations arithmétiques surréalistes, on peut montrer que c'est un corps ; et en montrant que chaque élément de Q est accessible à partir de S _* par une série finie (pas plus de deux, en fait) des opérations arithmétiques , y compris l' inversion multiplicatif , on peut montrer que Q est strictement plus petit que le sous - ensemble de S _w identifié avec les nombres réels .

L'ensemble S _ω a la même cardinalité que les nombres réels R . Ceci peut être démontré en exposant les mappages surjectifs de S _ω à l'unité de fermeture intervalle I de R et vice versa. Mapping S _w sur I est la routine; mapper les nombres inférieurs ou égaux à ε (y compris -ω) à 0, les nombres supérieurs ou égaux à 1-ε (y compris ω) à 1, et les nombres entre ε et 1-ε à leur équivalent dans I (mappage des voisins infinitésimaux y ±ε de chaque fraction dyadique y , avec y lui-même, à y ). Pour mapper I sur S _ω , mapper le tiers central (ouvert) (1/3, 2/3) de I sur { | } = 0; le tiers central (7/9, 8/9) du tiers supérieur à { 0 | } = 1 ; et ainsi de suite. Cela mappe un intervalle ouvert non vide de I sur chaque élément de S _* , de manière monotone. Le résidu de I consiste en l' ensemble de Cantor 2 ^ω , chaque point qui est identifié de manière unique par une cloison des intervalles central tiers en ensembles gauche et droit, ce qui correspond précisément à une forme { L | R } dans S _ω . Cela place l'ensemble de Cantor en correspondance un à un avec l'ensemble de nombres surréalistes avec l'anniversaire ω.

Induction transfinie

Continuer à effectuer une induction transfinie au-delà de S _ω produit plus de nombres ordinaux α, chacun étant représenté comme le plus grand nombre surréaliste ayant anniversaire α. (Il s'agit essentiellement d'une définition des nombres ordinaux résultant de l'induction transfinie.) Le premier de ces nombres ordinaux est ω+1 = { ω | }. Il existe un autre nombre infini positif dans la génération +1 :

−1 = { 1, 2, 3, 4, ... | }.

Le nombre surréaliste ω−1 n'est pas un ordinal ; l'ordinal n'est le successeur d'aucun ordinal. Il s'agit d'un nombre surréaliste d'anniversaire ω+1, qui est étiqueté ω−1 sur la base qu'il coïncide avec la somme de ω = { 1, 2, 3, 4, ... | } et -1 = { | 0}. De même, il y a deux nouveaux nombres infinitésimaux dans la génération ω+1 :

2ε = + ε = { ε | 1+ε, ¹ / ₂ +ε, ¹ / ₄ +ε, ¹ / ₈ +ε, ... } et

/2 = · ¹ / ₂ = { 0 | }.

À un stade ultérieur de l'induction transfinie, il existe un nombre supérieur à ω+ k pour tous les entiers naturels k :

2ω = ω + ω = { ω+1, ω+2, ω+3, ω+4, ... | }

Ce nombre peut être étiqueté ω + ω à la fois parce que son anniversaire est ω + ω (le premier nombre ordinal non accessible à partir de ω par l'opération successeur) et parce qu'il coïncide avec la somme surréaliste de ω et ω ; il peut aussi être étiqueté 2ω car il coïncide avec le produit de ω = { 1, 2, 3, 4, ... | } et 2 = { 1 | }. C'est le deuxième ordinal limite ; l'atteindre à partir de ω via l'étape de construction nécessite une induction transfinie sur . Cela implique une union infinie d'ensembles infinis, ce qui est une opération théorique des ensembles « plus forte » que l'induction transfinie précédente requise. ${\displaystyle \bigcup _{k<\omega }S_{\omega +k}}$

Notez que l' addition et la multiplication conventionnelles des ordinaux ne coïncident pas toujours avec ces opérations sur leurs représentations surréalistes. La somme des ordinaux 1 + est égale à ω, mais la somme surréaliste est commutative et produit 1 + ω = ω + 1 > ω. L'addition et la multiplication des nombres surréalistes associés aux ordinaux coïncident avec la somme naturelle et le produit naturel des ordinaux.

Tout comme 2ω est plus grand que ω + n pour tout entier naturel n , il existe un nombre surréaliste ω/2 qui est infini mais plus petit que ω − n pour tout entier naturel n . Autrement dit, /2 est défini par

/2 = { S _* | − S _* }

où à droite la notation x − Y est utilisée pour signifier { x − y  : y dans Y }. Il peut être identifié comme le produit de ω et de la forme { 0 | 1 } de ¹ / ₂ . L'anniversaire de ^ω / ₂ est l'ordinal limite ω2.

Puissances de et forme normale de Conway

Pour classer les "ordres" des nombres surréalistes infinis et infinitésimaux, également appelés classes archimédiennes , Conway associe à chaque nombre surréaliste x le nombre surréaliste

• ω ^x = {0, r ω ^{x _L} | s ω ^{x _R} },

où r et s s'étendent sur les nombres réels positifs. Si x < y alors ω ^y est « infiniment supérieur » à ω ^x , en ce sens qu'il est supérieur à r ω ^x pour tous les nombres réels r . Les puissances de satisfont également aux conditions

• ω ^x ω ^y = ω ^{x + y} ,
• ω ^{- x} = 1 / ω ^x ,

ils se comportent donc comme on s'attendrait à ce que les pouvoirs se comportent.

Chaque puissance de ω a également la caractéristique rédemptrice d'être le nombre surréaliste le plus simple de sa classe archimédienne ; à l'inverse, chaque classe archimédienne dans les nombres surréalistes contient un membre unique le plus simple. Ainsi, pour chaque nombre surréaliste positif x, il existera toujours un nombre réel positif r et un nombre surréaliste y de sorte que x − r ω ^y soit « infiniment plus petit » que x . L'exposant y est la « base ω logarithme » de x , défini sur les surréalistes positifs ; il peut être démontré que log _ω mappe les surréalistes positifs sur les surréalistes et que log _ω ( xy ) = log _ω ( x ) + log _ω ( y ).

Ceci est étendu par induction transfinie de sorte que chaque nombre surréaliste a une « forme normale » analogue à la forme normale de Cantor pour les nombres ordinaux. C'est la forme normale de Conway : chaque nombre surréaliste x peut être écrit de manière unique sous la forme

• x = r ₀ ω ^{y ₀} + r ₁ ω ^{y ₁} + ...,

où chaque r _α est un nombre réel non nul et les y _α s forment une séquence strictement décroissante de nombres surréalistes. Cette "somme", cependant, peut avoir une infinité de termes, et a en général la longueur d'un nombre ordinal arbitraire. (Zéro correspond bien sûr au cas d'une séquence vide, et est le seul nombre surréaliste sans exposant de tête.)

Vus de cette manière, les nombres surréalistes ressemblent à un champ de séries entières , sauf que les séquences décroissantes d'exposants doivent être limitées en longueur par un ordinal et ne peuvent pas être aussi longues que la classe des ordinaux. C'est la base de la formulation des nombres surréalistes comme une série de Hahn .

Lacunes et continuité

Contrairement aux nombres réels, un sous-ensemble (correct) des nombres surréalistes n'a pas de limite supérieure (ou inférieure) à moins qu'il n'ait un élément maximal (minimal). Conway définit un écart comme { L | R }, L < R , L ∪ R = 𝐍𝐨; ce n'est pas un nombre car au moins un des côtés est une classe appropriée. Bien que similaires, les écarts ne sont pas tout à fait les mêmes que les sections de Dedekind , mais nous pouvons toujours parler d'un achèvement 𝐍𝐨 ^𝕯 des nombres surréalistes avec l'ordre naturel qui est un continuum linéaire (de la taille appropriée de la classe) .

Par exemple, il n'y a pas de surréaliste infini le moins positif, mais l'écart ∞ = { x : ∃ n ∈ : x < n | x : ∀ n ∈ : x > n } est supérieur à tous les nombres réels et inférieur à tous les surréalistes infinis positifs, et est donc la plus petite borne supérieure des réels dans 𝐍𝐨 ^𝕯 . De même l'écart 𝐎𝐧 = { 𝐍𝐨 | } est plus grand que tous les nombres surréalistes. (Ceci est un jeu de mots ésotérique : Dans la construction générale des ordinaux, α "est" l'ensemble des ordinaux plus petit que α et nous pouvons utiliser cette équivalence pour écrire α = { α | } dans les surréalistes ; 𝐎𝐧 désigne la classe des nombres ordinaux , et parce que 𝐎𝐧 est cofinal dans 𝐍𝐨 nous avons {𝐍𝐨 |} = {𝐎𝐧 |} = 𝐎𝐧 par extension). ${\displaystyle \mathbb {N} }$${\displaystyle \mathbb {N} }$

Avec un peu de soin en théorie des ensembles, 𝐍𝐨 peut être équipé d'une topologie où les ensembles ouverts sont des unions d'intervalles ouverts (indexés par des ensembles appropriés) et des fonctions continues peuvent être définies. Un équivalent des séquences de Cauchy peut également être défini bien qu'elles doivent être indexées par la classe des ordinaux ; ceux - ci convergent toujours, mais la limite peut être soit un nombre ou un intervalle qui peut être exprimée sous la forme Σ _{α∈𝐍𝐨} r _α co ^{un _α} avec une _α décroissante et possédant pas inférieur lié à 𝐍𝐨. (Tous ces espaces peuvent être compris comme des séquences de Cauchy elles-mêmes, mais il existe d'autres types d'espaces qui ne sont pas des limites, tels que ∞ et 𝐎𝐧).

Fonction exponentielle

Sur la base des travaux inédits de Kruskal , une construction (par induction transfinie) qui étend la fonction exponentielle réelle exp( x ) (de base e ) aux surréalistes a été réalisée par Gonshor.

Autres exponentielles

La fonction puissances de est également une fonction exponentielle, mais n'a pas les propriétés souhaitées pour une extension de la fonction sur les réels. Elle sera cependant nécessaire dans le développement de l' exponentielle de base e , et c'est cette fonction qui est visée chaque fois que la notation ω ^x est utilisée dans la suite.

Lorsque y est une fraction dyadique, la fonction puissance x ∈ No , x ↦ x ^y peut être composée d'une multiplication, d'un inverse multiplicatif et d'une racine carrée, qui peuvent tous être définis de manière inductive. Ses valeurs sont complètement déterminées par la relation de base x ^y+z = x ^y ·x ^z , et lorsqu'elle est définie, elle s'accorde nécessairement avec toute autre exponentiation qui peut exister.

Induction de base

Les étapes d'induction pour l'exponentielle surréaliste sont basées sur le développement en série pour l'exponentielle réelle, exp x = Σ _{n 0} x ⁿ /n!, plus précisément ces sommes partielles qui peuvent être montrées par l'algèbre de base comme étant positives mais inférieures à toutes plus tard. Pour x positif, ceux-ci sont notés [ x ] _n et incluent toutes les sommes partielles ; pour x négatif mais fini, [ x ] _{2 n +1} désigne les pas impairs de la série à partir du premier avec une partie réelle positive (qui existe toujours). Pour x négatif infini, les sommes partielles impaires sont strictement décroissantes et la notation [ x ] _{2 n +1} dénote l'ensemble vide, mais il s'avère que les éléments correspondants ne sont pas nécessaires dans l'induction.

Les relations qui tiennent pour réel x < y sont alors exp x · [ y–x ] _n < exp y et exp y · [ x–y ] _{2 n +1} < exp x , et cela peut être étendu aux surréalistes avec le définition exp z = { 0, exp z _L · [ z–z _L ] _n , exp z _R · [ z–z _R ] _{2 n +1} | exp z _R / [ z _R –z ] _n , exp z _L / [ z _L –z ] _{2 n +1} }. Ceci est bien défini pour tous les arguments surréalistes (la valeur existe et ne dépend pas du choix de z _L et z _R ).

Résultats

En utilisant cette définition, ce qui suit est valable :

• exp est une fonction positive strictement croissante, x < y ⇒ 0 < exp x < exp y
• exp satisfait exp( x + y ) = exp x · exp y
• exp est une surjection (sur No ₊ ) et a un inverse bien défini, log = exp ^–1
• exp coïncide avec la fonction exponentielle habituelle sur les réels (et donc exp 0 = 1, exp 1 = e )
• Pour x infinitésimal, la valeur de la série formelle formelle Σ _{n ≥0} x ⁿ / n ! est bien défini et coïncide avec la définition inductive
  • Lorsque x est donné sous forme normale de Conway, l'ensemble des exposants du résultat est bien ordonné et les coefficients sont des sommes finies, donnant directement la forme normale du résultat (qui a un premier 1)
  • De même, pour x infiniment proche de 1, log x est donné par le développement en séries entières de x –1
• Pour x infini positif , exp x est également infini
  • Si x a la forme ω ^α (α > 0), exp x a la forme ω ^{ω β} où β est une fonction strictement croissante de α. En fait il existe une bijection définie inductivement g : No ₊ → No : α ↦ β dont l'inverse peut aussi être défini inductivement
  • Si x est "pur infini" de forme normale x = Σ _α<β r _α ω ^{a _α} où tout a _α > 0 , alors exp x = ω ^{Σ _α<β r _α ω g ( a _α )}
  • De même, pour x = ω ^{Σ _α<β r _α ω b _α} , l'inverse est donné par log x = Σ _α<β r _α ω ^{g –1 (b _α )}
• Tout nombre surréaliste peut être écrit comme la somme d'un infini pur, d'un réel et d'une partie infinitésimale, et l'exponentielle est le produit des résultats partiels donnés ci-dessus
  • La forme normale peut être écrite en multipliant la partie infinie (une seule puissance de ) et l'exponentielle réelle dans la série de puissances résultant de l'infinitésimal
  • A l' inverse, en divisant le premier terme de la forme normale apportera un nombre irréel dans la forme (co ^{Σ _{γ <δ} t _γ co b _γ} ) · r · (1 + Σ _{α <β} s _α co ^{un _α} ) , pour une _α <0 , où chaque facteur a une forme pour laquelle un moyen de calcul du logarithme a été donnée ci - dessus; la somme est alors le logarithme général
    • Bien qu'il n'y ait pas de définition inductive générale de log (contrairement à exp), les résultats partiels sont donnés en termes de telles définitions. De cette façon, le logarithme peut être calculé explicitement, sans référence au fait que c'est l'inverse de l'exponentielle.
• La fonction exponentielle est beaucoup plus grande que toute puissance finie
  • Pour tout x infini positif et tout fini n , exp( x )/ x ⁿ est infini
  • Pour tout entier n et surréaliste x > n ² , exp( x ) > x ⁿ . Cette contrainte plus forte est l'un des axiomes de Ressayre pour le champ exponentiel réel
• exp satisfait tous les axiomes de Ressayre pour le champ exponentiel réel
  • Les surréalistes à exponentielle est une extension élémentaire du champ exponentiel réel
  • Pour ε _β un nombre ordinal epsilon, l'ensemble des nombres surréalistes dont l'anniversaire est inférieur à ε _β constitue un corps fermé sous les exponentielles, et est également une extension élémentaire du vrai champ exponentiel

Exemples

L'exponentielle surréaliste est essentiellement donnée par son comportement sur les puissances positives de , c'est-à-dire la fonction g(a) , combinée à un comportement bien connu sur les nombres finis. Seuls des exemples de la première seront donnés. De plus, g(a) = a est valable pour une grande partie de son intervalle, par exemple pour tout nombre fini avec une partie réelle positive et tout nombre infini inférieur à une puissance itérée de ω ( ω ^{ω · · ω} pour un certain nombre de niveaux).

• exp = ω ^ω
• exp ^1/ω = ω et log ω = ω ^1/ω
• exp (ω · log ω) = exp (ω · ω ^1/ω ) = ω ^{ω (1 + 1/ω)}
  • Cela montre que la fonction "puissance de " n'est pas compatible avec exp, car la compatibilité exigerait une valeur de ω ^ω ici
• exp ε ₀ = ω ^{ω ε ₀ + 1}
• log ε ₀ = ε ₀ / ω

Exponentiation

Une exponentiation générale peut être définie comme x ^y = exp( y · log x ) , donnant une interprétation à des expressions comme 2 ^ω = exp(ω · log 2) = ω ^{log 2 · ω} . Encore une fois, il est essentiel de distinguer cette définition de la fonction "puissances de ", surtout si ω peut apparaître comme base.

Nombres surcomplexes

Un nombre surcomplexe est un nombre de la forme a + b i , où a et b sont des nombres surréalistes et i est la racine carrée de −1 . Les numéros surcomplex forment un algébriquement clos champ (sauf pour être une classe appropriée), isomorphe à la clôture algébrique du champ généré par l' extension des nombres rationnels par une classe appropriée de algébriquement indépendants transcendantales éléments. Jusqu'à l' isomorphisme de champ , ce fait caractérise le champ des nombres surcomplexes au sein de toute théorie des ensembles fixes.

Jeux

La définition des nombres surréalistes contenait une restriction : chaque élément de L doit être strictement inférieur à chaque élément de R. Si cette restriction est supprimée, nous pouvons générer une classe plus générale connue sous le nom de jeux . Tous les jeux sont construits selon cette règle :

Règle de construction
Si L et R sont deux ensembles de jeux alors { L | R } est un jeu.

L'addition, la négation et la comparaison sont toutes définies de la même manière pour les nombres surréalistes et les jeux.

Chaque nombre surréaliste est un jeu, mais tous les jeux ne sont pas des nombres surréalistes, par exemple le jeu { 0 | 0 } n'est pas un nombre surréaliste. La classe de jeux est plus générale que les surréalistes et a une définition plus simple, mais il lui manque certaines des propriétés les plus agréables des nombres surréalistes. La classe des nombres surréalistes forme un champ , mais pas la classe des jeux. Les surréalistes ont un ordre total : étant donné deux surréalistes, ils sont soit égaux, soit l'un est plus grand que l'autre. Les jeux n'ont qu'un ordre partiel : il existe des paires de jeux qui ne sont ni égaux, ni supérieurs, ni inférieurs les uns aux autres. Chaque nombre surréaliste est soit positif, négatif ou nul. Chaque jeu est soit positif, négatif, nul ou flou (incomparable à zéro, comme {1|−1}).

Un coup dans un jeu implique le joueur dont le coup est de choisir un jeu parmi ceux disponibles en L (pour le joueur de gauche) ou R (pour le joueur de droite) puis de passer ce jeu choisi à l'autre joueur. Un joueur qui ne peut pas se déplacer parce que le choix est dans l'ensemble vide a perdu. Un jeu positif représente une victoire pour le joueur gauche, un jeu négatif pour le joueur droit, un jeu zéro pour le deuxième joueur à déplacer et un jeu flou pour le premier joueur à déplacer.

Si x , y et z sont surréalistes et x = y , alors x z = y z . Cependant, si x , y et z sont des jeux, et x = y , alors il n'est pas toujours vrai que x z = y z . Notez que "=" signifie ici égalité, pas identité.

Application à la théorie combinatoire des jeux

Les nombres surréalistes ont été à l'origine motivés par des études sur le jeu Go , et il existe de nombreux liens entre les jeux populaires et les surréalistes. Dans cette section, nous utiliserons un jeu en majuscules pour l'objet mathématique {L|R}, et le jeu en minuscules pour les jeux récréatifs comme les échecs ou le go .

On considère des jeux avec ces propriétés :

• Deux joueurs (nommés Gauche et Droite )
• Déterministe (le jeu à chaque étape dépendra entièrement des choix des joueurs, plutôt que d'un facteur aléatoire)
• Aucune information cachée (comme des cartes ou des tuiles qu'un joueur cache)
• Les joueurs se relaient à tour de rôle (le jeu peut autoriser ou non plusieurs mouvements dans un tour)
• Chaque partie doit se terminer en un nombre fini de coups
• Dès qu'il ne reste plus de coups légaux pour un joueur, le jeu se termine et ce joueur perd

Pour la plupart des jeux, la position initiale du plateau ne donne aucun grand avantage à l'un ou l'autre des joueurs. Au fur et à mesure que le jeu progresse et qu'un joueur commence à gagner, des positions sur le plateau se produiront dans lesquelles ce joueur a un net avantage. Pour analyser les jeux, il est utile d'associer un jeu à chaque position du plateau. La valeur d'une position donnée sera le Jeu {L|R}, où L est l'ensemble des valeurs de toutes les positions qui peuvent être atteintes en un seul coup par Gauche. De même, R est l'ensemble des valeurs de toutes les positions qui peuvent être atteintes en un seul coup par Droite.

Le jeu zéro (appelé 0) est le jeu où L et R sont tous les deux vides, de sorte que le joueur suivant (L ou R) perd immédiatement. La somme de deux jeux G = { L1 | R1 } et H = { L2 | R2 } est défini comme le Jeu G + H = { L1 + H, G + L2 | R1 + H, G + R2 } où le joueur à déplacer choisit dans lequel des jeux jouer à chaque étape, et le perdant est toujours le joueur qui se retrouve sans mouvement légal. On peut imaginer deux échiquiers entre deux joueurs, les joueurs jouant alternativement, mais en toute liberté quant à l'échiquier sur lequel jouer. Si G est le Jeu {L | R}, -G est le Jeu {-R | -L}, c'est-à-dire avec le rôle des deux joueurs inversé. Il est facile de montrer G - G = 0 pour tous les jeux G (où G - H est défini comme G + (-H)).

Cette façon simple d'associer des jeux à des jeux donne un résultat très intéressant. Supposons que deux joueurs parfaits jouent un jeu commençant par une position donnée dont le jeu associé est x . Nous pouvons classer tous les jeux en quatre classes comme suit :

• Si x > 0, Left gagnera, quel que soit le joueur qui joue en premier.
• Si x < 0, alors Right gagnera, quel que soit le joueur qui joue en premier.
• Si x = 0 alors le joueur qui va en second gagnera.
• Si x || 0 alors le joueur qui joue le premier gagnera.

Plus généralement, nous pouvons définir G > H comme G - H > 0, et de même pour <, = et ||.

La notation G || H signifie que G et H sont incomparables. G || H est équivalent à G−H || 0, c'est-à-dire que G > H, G < H et G = H sont tous faux. On dit parfois que des jeux incomparables se confondent entre eux, car l'un ou l'autre peut être préféré par un joueur en fonction de ce qu'on y ajoute. Un jeu confondu avec zéro est dit flou , par opposition à positif, négatif ou zéro . Un exemple de jeu flou est l' étoile (*) .

Parfois, lorsqu'une partie touche à sa fin, elle se décomposera en plusieurs parties plus petites qui n'interagissent pas, sauf que le tour de chaque joueur ne permet de se déplacer que dans l'une d'entre elles. Par exemple, au Go, le plateau se remplira lentement de pièces jusqu'à ce qu'il n'y ait plus que quelques petites îles d'espace vide où un joueur peut se déplacer. Chaque île est comme un jeu de go séparé, joué sur un très petit plateau. Il serait utile que chaque sous-jeu puisse être analysé séparément, puis les résultats combinés pour donner une analyse de l'ensemble du jeu. Cela ne semble pas facile à faire. Par exemple, il peut y avoir deux sous-jeux où celui qui bouge en premier gagne, mais lorsqu'ils sont combinés en un seul gros jeu, ce n'est plus le premier joueur qui gagne. Heureusement, il existe un moyen de faire cette analyse. Le théorème suivant peut être appliqué :

Si un grand jeu se décompose en deux jeux plus petits et que les petits jeux ont des jeux associés de x et y , alors le grand jeu aura un jeu associé de x + y .

Un jeu composé de jeux plus petits est appelé la somme disjonctive de ces jeux plus petits, et le théorème stipule que la méthode d'addition que nous avons définie équivaut à prendre la somme disjonctive des addendes.

Historiquement, Conway a développé la théorie des nombres surréalistes dans l'ordre inverse de la façon dont elle a été présentée ici. Il analysait les phases finales de Go et s'est rendu compte qu'il serait utile d'avoir un moyen de combiner les analyses des sous-jeux sans interaction dans une analyse de leur somme disjonctive . De là, il a inventé le concept d'un jeu et l'opérateur d'addition pour celui-ci. De là, il est passé à l'élaboration d'une définition de la négation et de la comparaison. Puis il remarqua qu'une certaine classe de Jeux avait des propriétés intéressantes ; cette classe est devenue les nombres surréalistes. Enfin, il a développé l'opérateur de multiplication et a prouvé que les surréalistes sont en fait un champ, et qu'il comprend à la fois les réels et les ordinaux.

Réalisations alternatives

Des approches alternatives aux nombres surréalistes complètent l'exposition de Conway en termes de jeux.

Extension de signe

Définitions

Dans ce qu'on appelle maintenant le développement de signe ou la suite de signes d'un nombre surréaliste, un nombre surréaliste est une fonction dont le domaine est un ordinal et dont le codomaine est { -1, +1 }. Ceci est équivalent aux séquences LR de Conway.

Définir le prédicat binaire "plus simple que" sur les nombres par x est plus simple que y si x est un sous - ensemble propre de y , c'est -à- dire si dom( x ) < dom( y ) et x (α) = y (α) pour tout α < dom( x ).

Pour les nombres surréalistes, définissez la relation binaire < comme un ordre lexicographique (avec la convention que les "valeurs non définies" sont supérieures à -1 et inférieures à 1). Donc x < y si l'une des conditions suivantes est vérifiée :

• x est plus simple que y et y (dom( x )) = + 1;
• y est plus simple que x et x (dom( y )) = − 1;
• il existe un nombre z tel que z est plus simple que x , z est plus simple que y , x (dom( z )) = − 1 et y (dom( z )) = + 1.

De manière équivalente, soit δ( x , y ) = min({ dom( x ), dom( y )} ∪ { α : α < dom( x ) ∧ α < dom( y ) ∧ x (α) ≠ y (α) }), de sorte que x = y si et seulement si δ( x , y ) = dom( x ) = dom( y ). Alors, pour les nombres x et y , x < y si et seulement si l'une des conditions suivantes est vérifiée :

• ( x , y ) = dom( x ) ∧ δ( x , y ) < dom( y ) ∧ y (δ( x , y )) = + 1;
• ( x , y ) < dom( x ) ∧ ( x , y ) = dom( y ) ∧ x (δ( x , y )) = − 1;
• δ( x , y ) < dom( x ) ∧ δ( x , y ) < dom( y ) ∧ x (δ( x , y )) = − 1 ∧ y (δ( x , y )) = + 1.

Pour les nombres x et y , x ≤ y si et seulement si x < y ∨ x = y , et x > y si et seulement si y < x . Aussi x ≥ y , si et seulement si y ≤ x .

La relation < est transitive , et pour tous les nombres x et y , exactement l'un des x < y , x = y , x > y , est vrai (loi de la trichotomie ). Cela signifie que < est un ordre linéaire (sauf que < est une classe appropriée).

Pour des ensembles de nombres, L et R tels que ∀ x ∈ L ∀ y ∈ R ( x < y ), il existe un nombre unique z tel que

• ∀ x ∈ L ( x < z ) ∧ ∀ y ∈ R ( z < y ),
• Pour tout nombre w tel que ∀ x ∈ L ( x < w ) ∧ ∀ y ∈ R ( w < y ), w = z ou z est plus simple que w .

De plus, z est constructible à partir de L et R par induction transfinie. z est le nombre le plus simple entre L et R . Soit le nombre unique z noté σ( L , R ).

Pour un nombre x , définissez son ensemble gauche L ( x ) et son ensemble droit R ( x ) par

• L ( x ) = { x | _α  : α <dom ( x ) ∧ x (α) = + 1};
• R ( x ) = { x | _α  : α <dom ( x ) ∧ x (α) = - 1},

alors σ( L ( x ), R ( x )) = x .

Un avantage de cette réalisation alternative est que l'égalité est l'identité, pas une relation définie par induction. Contrairement à la réalisation de Conway des nombres surréalistes, cependant, l'expansion de signe nécessite une construction préalable des ordinaux, tandis que dans la réalisation de Conway, les ordinaux sont construits comme des cas particuliers de surréalistes.

Cependant, des définitions similaires peuvent être faites qui éliminent le besoin de construction préalable des ordinaux. Par exemple, nous pourrions laisser les surréalistes être la classe (définie récursivement) de fonctions dont le domaine est un sous-ensemble des surréalistes satisfaisant la règle de transitivité ∀ g ∈ dom f (∀ h ∈ dom g ( h ∈ dom f )) et dont la plage est { −, + }. "Plus simple que" est défini très simplement maintenant — x est plus simple que y si x dom y . L'ordre total est défini en considérant x et y comme des ensembles de paires ordonnées (comme une fonction est normalement définie) : Soit x = y , soit le nombre surréaliste z = x ∩ y est dans le domaine de x ou dans le domaine de y (ou les deux, mais dans ce cas les signes doivent être en désaccord). On a alors x < y si x ( z ) = − ou y ( z ) = + (ou les deux). La conversion de ces fonctions en séquences de signes est une tâche simple ; ranger les éléments de dom f par ordre de simplicité (c'est-à-dire d'inclusion), puis noter les signes que f attribue à chacun de ces éléments dans l'ordre. Les ordinaux apparaissent alors naturellement comme ces nombres surréalistes dont la plage est { + }.

Addition et multiplication

La somme x + y de deux nombres, x et y , est définie par induction sur dom( x ) et dom( y ) par x + y = ( L , R ), où

• L = { u + y  : u ∈ L ( x )} ∪ { x + v  : v ∈ L ( y )},
• R = { u + y  : u ∈ R ( x )} ∪ { x + v  : v ∈ R ( y )}.

L'identité additive est donnée par le nombre 0 = { }, c'est-à - dire que le nombre 0 est l'unique fonction dont le domaine est l'ordinal 0, et l'inverse additif du nombre x est le nombre − x , donné par dom(− x ) = dom( x ), et, pour α < dom( x ), (− x )(α) = − 1 si x (α) = + 1, et (− x )(α) = + 1 si x (α) = − 1.

Il s'ensuit qu'un nombre x est positif si et seulement si 0 < dom( x ) et x (0) = + 1, et x est négatif si et seulement si 0 < dom( x ) et x (0) = − 1.

Le produit xy de deux nombres, x et y , est défini par induction sur dom( x ) et dom( y ) par xy = ( L , R ), où

• L = { uy + xv - uv  : u ∈ L ( x ), v ∈ L ( y )} ∪ { uy + xv - uv  : u ∈ R ( x ), v ∈ R ( y )},
• R = { uy + xv - uv  : u ∈ L ( x ), v ∈ R ( y )} ∪ { uy + xv - uv  : u ∈ R ( x ), v ∈ L ( y )}.

L'identité multiplicative est donnée par le nombre 1 = { (0,+1) }, c'est -à- dire que le nombre 1 a un domaine égal à l'ordinal 1, et 1(0) = + 1.

Correspondance avec la réalisation de Conway

L'application de la réalisation de Conway aux développements de signe est donnée par f ({ L | R }) = σ( M , S ), où M = { f ( x ) : x ∈ L } et S = { f ( x ) : x ∈ R }.

L'application inverse de la réalisation alternative à la réalisation de Conway est donnée par g ( x ) = { L | R }, où L = { g ( y ): y ∈ L ( x )} et R = { g ( y ): y ∈ R ( x )}.

Approche axiomatique

Dans une autre approche des surréalistes, donnée par Alling, la construction explicite est complètement contournée. Au lieu de cela, un ensemble d'axiomes est donné que toute approche particulière des surréalistes doit satisfaire. Tout comme l' approche axiomatique des réels, ces axiomes garantissent l'unicité jusqu'à l'isomorphisme.

Un triple est un système de nombres surréaliste si et seulement si ce qui suit est vrai : ${\displaystyle \langle \mathbf {Non} ,\mathrm {<} ,b\rangle }$

• < est une commande totale supérieure à Non
• b est une fonction de No sur la classe de tous les ordinaux ( b est appelée la "fonction d'anniversaire" sur No ).
• Soient A et B des sous-ensembles de No tels que pour tout x ∈ A et y ∈ B , x < y (en utilisant la terminologie d'Alling, 〈A , B〉 est une "coupe de Conway" de No ). Alors il existe un unique z ∈ No tel que b(z) est minimal et pour tout x ∈ A et tout y ∈ B , x < z < y . (Cet axiome est souvent appelé « théorème de simplicité de Conway ».)
• De plus, si un ordinal α est supérieur à b(x) pour tout x ∈ A , B , alors b(z) ≤ α . (Alling appelle un système qui satisfait cet axiome un "système de nombres surréaliste complet".)

La construction originale de Conway et la construction de signes d'expansion des surréalistes satisfont à ces axiomes.

Compte tenu de ces axiomes, Alling tire la définition originale de Conway de et développe une arithmétique surréaliste.

Hiérarchie de simplicité

Une construction des nombres surréalistes en tant que pseudo-arbre binaire maximal avec simplicité (ancêtre) et relations d'ordre est due à Philip Ehrlich, La différence avec la définition habituelle d'un arbre est que l'ensemble des ancêtres d'un sommet est bien ordonné, mais peut ne pas avoir d'élément maximal (prédécesseur immédiat) ; en d'autres termes, le type d'ordre de cet ensemble est un nombre ordinal général, pas seulement un nombre naturel. Cette construction remplit également les axiomes d'Alling et peut facilement être mappée à la représentation de la séquence de signes.

série Hahn

Alling prouve également que le champ des nombres surréalistes est isomorphe (en tant que champ ordonné) au champ des séries de Hahn avec des coefficients réels sur le groupe de valeurs des nombres surréalistes eux-mêmes (la représentation en série correspondant à la forme normale d'un nombre surréaliste, tel que défini dessus). Cela établit un lien entre les nombres surréalistes et les approches mathématiques plus conventionnelles de la théorie des champs ordonnés.

Cet isomorphisme transforme les nombres surréalistes en un champ valorisé où l'évaluation est l'inverse additif de l'exposant du terme dominant dans la forme normale de Conway, par exemple, (ω) = -1. L'anneau d'évaluation est alors constitué des nombres surréalistes finis (nombres avec une partie réelle et/ou infinitésimale). La raison de l'inversion de signe est que les exposants de la forme normale de Conway constituent un ensemble inversé bien ordonné, alors que les séries de Hahn sont formulées en termes de sous-ensembles (non inversés) bien ordonnés du groupe de valeurs.

Relation avec les hyperréels

Philip Ehrlich a construit un isomorphisme entre le champ de nombres surréaliste maximal de Conway et les hyperréels maximaux dans la théorie des ensembles de von Neumann-Bernays-Gödel .

Voir également

• Nombre hyperréel
• Analyse non standard

Remarques

Les références

Lectures complémentaires

• Exposition originale de Donald Knuth : Surreal Numbers: How Two Ex-Students Turned on Pure Mathematics and Found Total Happiness , 1974, ISBN  0-201-03812-9 . Plus d'informations peuvent être trouvées sur la page d'accueil officielle du livre .
• Une mise à jour du livre classique de 1976 définissant les nombres surréalistes et explorant leurs liens avec les jeux : John Conway, On Numbers And Games , 2e éd., 2001, ISBN  1-56881-127-6 .
• Une mise à jour de la première partie du livre de 1981 qui présentait les nombres surréalistes et l'analyse des jeux à un public plus large : Berlekamp, ​​Conway et Guy, Winning Ways for Your Mathematical Plays , vol. 1, 2e éd., 2001, ISBN  1-56881-130-6 .
• Martin Gardner , Penrose Tiles to Trapdoor Ciphers, WH Freeman & Co., 1989, ISBN  0-7167-1987-8 , chapitre 4. Un aperçu non technique; réimpression de l' article de 1976 du Scientific American .
• Polly Shulman, "Infinity Plus One, and Other Surreal Numbers" , Discover , décembre 1995.
• Un traitement détaillé des nombres surréalistes : Norman L. Alling, Foundations of Analysis over Surreal Number Fields , 1987, ISBN  0-444-70226-1 .
• Un traitement des surréalistes basé sur la réalisation de l'expansion du signe : Harry Gonshor, An Introduction to the Theory of Surreal Numbers , 1986, ISBN  0-521-31205-1 .
• Un développement philosophique détaillé du concept de nombres surréalistes en tant que concept de nombre le plus général : Alain Badiou , Number and Numbers , New York : Polity Press, 2008, ISBN  0-7456-3879-1 (broché), ISBN  0-7456- 3878-3 (couverture rigide).
• Le programme des fondations univalentes (2013). Théorie des types d'homotopie : fondements univalents des mathématiques . Princeton, NJ : Institut d'études avancées . MR  3204653 .Les nombres surréalistes sont étudiés dans le contexte de la théorie des types d'homotopie dans la section 11.6.

Liens externes

• Hackenstrings, et le 0.999... ?= 1 FAQ, par AN Walker , une archive de l'original disparu
• Une introduction douce mais complète par Claus Tøndering
• Good Math, Bad Math: Surreal Numbers , une série d'articles sur les nombres surréalistes et leurs variations