Solide d'Archimède - Archimedean solid

Tétraèdre tronqué , cuboctaèdre et icosidodécaèdre tronqué . Le premier et le dernier peuvent être décrits comme le plus petit et le plus grand solide d'Archimède, respectivement.
Rhombicuboctaèdre et pseudo-rhombicuboctaèdre

En géométrie , un solide d'Archimède est l'un des 13 solides énumérés pour la première fois par Archimède . Ce sont les polyèdres uniformes convexes composés de polygones réguliers se rencontrant en des sommets identiques , excluant les cinq solides platoniciens (qui ne sont composés que d'un seul type de polygone) et excluant les prismes et les antiprismes . Ils diffèrent des solides de Johnson , dont les faces polygonales régulières ne se rencontrent pas en des sommets identiques.

"Sommets identiques" signifie que chacun des deux sommets est symétrique l'un de l'autre : Une isométrie globale de l'ensemble du solide prend un sommet à l'autre tout en posant le solide directement sur sa position initiale. Branko Grünbaum  ( 2009 ) a observé qu'un 14e polyèdre, la gyrobicupole carrée allongée (ou pseudo-rhombicuboctaèdre), répond à une définition plus faible d'un solide d'Archimède, dans lequel « sommets identiques » signifie simplement que les faces entourant chaque sommet sont du même type (c'est-à-dire que chaque sommet se ressemble de près), donc seule une isométrie locale est requise. Grünbaum a signalé une erreur fréquente dans laquelle les auteurs définissent les solides d'Archimède en utilisant cette définition locale mais omettent le 14e polyèdre. Si seulement 13 polyèdres doivent être répertoriés, la définition doit utiliser les symétries globales du polyèdre plutôt que les voisinages locaux.

Les prismes et antiprismes , dont les groupes de symétrie sont les groupes dièdres , ne sont généralement pas considérés comme des solides d'Archimède, même si leurs faces sont des polygones réguliers et que leurs groupes de symétrie agissent transitivement sur leurs sommets. En excluant ces deux familles infinies, il existe 13 solides d'Archimède. Tous les solides d'Archimède (mais pas la gyrobicupole carrée allongée) peuvent être réalisés via des constructions de Wythoff à partir des solides platoniciens à symétrie tétraédrique , octaédrique et icosaédrique .

Origine du nom

Les solides d'Archimède tirent leur nom d' Archimède , qui en a parlé dans un ouvrage aujourd'hui perdu. Pappus y fait référence, déclarant qu'Archimède a répertorié 13 polyèdres. Au cours de la Renaissance , les artistes et les mathématiciens valorisaient les formes pures à haute symétrie et, vers 1620, Johannes Kepler avait achevé la redécouverte des 13 polyèdres, ainsi que la définition des prismes , des antiprismes et des solides non convexes connus sous le nom de polyèdres de Kepler-Poinsot. . (Voir Schreiber, Fischer & Sternath 2008 pour plus d'informations sur la redécouverte des solides d'Archimède pendant la renaissance.)

Kepler a peut-être également trouvé la gyrobicupole carrée allongée (pseudorhombicuboctaèdre) : au moins, il a déclaré une fois qu'il y avait 14 solides d'Archimède. Cependant, son énumération publiée ne comprend que les 13 polyèdres uniformes, et la première déclaration claire de l'existence du pseudorhombicuboctaèdre a été faite en 1905, par Duncan Sommerville .

Classification

Il y a 13 solides d'Archimède (sans compter la gyrobicupole carrée allongée ; 15 si les images miroir de deux énantiomorphes , le cube snub et le dodécaèdre snub, sont comptées séparément).

Ici, la configuration des sommets fait référence au type de polygones réguliers qui se rencontrent à un sommet donné. Par exemple, une configuration de sommet de (4,6,8) signifie qu'un carré , un hexagone et un octogone se rencontrent à un sommet (l'ordre étant pris dans le sens des aiguilles d'une montre autour du sommet).

Nom/
(autre nom) 		Schläfli
Coxeter 		Transparent Solide Rapporter Vertex
conf. / fig. 		Visages Bords Vert. Volume
(arêtes de l'unité)
Groupe de points 		Sphéricité
tétraèdre tronqué t{3,3}
Nœud CDel 1.pngCDel 3.pngNœud CDel 1.pngCDel 3.pngCDel node.png 		Tétraèdre tronqué   Cog-scripted-svg-blue.svg Polyèdre tronqué 4a max.png Polyèdre tronqué 4a net.svg 3.6.6
Polyèdre tronqué 4a vertfig.png 		8 4 triangles
4 hexagones 		18 12 2.710 576 T d 0,775 4132
cuboctaèdre
(rhombitetratetraèdre, gyrobicupole triangulaire)		 r{4,3} ou rr{3,3}
CDel node.pngCDel 4.pngNœud CDel 1.pngCDel 3.pngCDel node.png ou Nœud CDel 1.pngCDel 3.pngCDel node.pngCDel 3.pngNœud CDel 1.png 		Cuboctaèdre   Cog-scripted-svg-blue.svg Polyèdre 6-8 max.png Polyèdre 6-8 net.svg 3.4.3.4
Polyèdre 6-8 vertfig.png 		14 8 triangles
6 carrés 		24 12 2.357 023 O h 0,904 9972
cube tronqué t{4,3}
Nœud CDel 1.pngCDel 4.pngNœud CDel 1.pngCDel 3.pngCDel node.png 		Hexaèdre tronqué   Cog-scripted-svg-blue.svg Polyèdre tronqué 6 max.png Polyèdre tronqué 6 net.svg 3.8.8
Polyèdre tronqué 6 vertfig.png 		14 8 triangles
6 octogones 		36 24 13,599 663 O h 0,849 4937
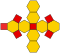
octaèdre tronqué
(tétratétraèdre tronqué)		 t{3,4} ou tr{3,3}
Nœud CDel 1.pngCDel 3.pngNœud CDel 1.pngCDel 4.pngCDel node.png ou Nœud CDel 1.pngCDel 3.pngNœud CDel 1.pngCDel 3.pngNœud CDel 1.png 		Octaèdre tronqué   Cog-scripted-svg-blue.svg Polyèdre tronqué 8 max.png Polyèdre tronqué 8 net.svg 4.6.6
Polyèdre tronqué 8 vertfig.png 		14 6 carrés
8 hexagones 		36 24 11.313 709 O h 0,909 9178
rhombicuboctaèdre
(petit rhombicuboctaèdre, orthobicupole carrée allongée)		 rr{4,3}
Nœud CDel 1.pngCDel 4.pngCDel node.pngCDel 3.pngNœud CDel 1.png 		Rhombicuboctaèdre   Cog-scripted-svg-blue.svg Polyèdre petit losange 6-8 max.png Polyèdre petit losange 6-8 net.svg 3.4.4.4
Polyèdre petit losange 6-8 vertfig.png 		26 8 triangles
18 carrés 		48 24 8.714 045 O h 0,954 0796
cuboctaèdre tronqué
(grand rhombicuboctaèdre)		 tr{4,3}
Nœud CDel 1.pngCDel 4.pngNœud CDel 1.pngCDel 3.pngNœud CDel 1.png 		Cuboctaèdre tronqué   Cog-scripted-svg-blue.svg Polyèdre grand losange 6-8 max.png Polyèdre grand losange 6-8 net.svg 4.6.8
Polyèdre grand losange 6-8 vertfig light.png 		26 12 carrés
8 hexagones
6 octogones 		72 48 41.798 990 O h 0,943 1657
cube snub
(snub cuboctaèdre)		 sr{4,3}
Nœud CDel h.pngCDel 4.pngNœud CDel h.pngCDel 3.pngNœud CDel h.png 		Snub hexaèdre (Ccw)   Cog-scripted-svg-blue.svg Polyèdre snub 6-8 gauche max.png Polyèdre snob 6-8 gauche net.svg 3.3.3.3.4
Polyèdre snub 6-8 gauche vertfig.png 		38 32 triangles
6 carrés 		60 24 7.889 295 O 0,965 1814
icosidodécaèdre
(gyrobirotunda pentagonale)		 r{5,3}
CDel node.pngCDel 5.pngNœud CDel 1.pngCDel 3.pngCDel node.png 		Icosidodécaèdre   Cog-scripted-svg-blue.svg Polyèdre 12-20 max.png Polyèdre 12-20 net.svg 3.5.3.5
Polyèdre 12-20 vertfig.png 		32 20 triangles
12 pentagones 		60 30 13.835 526 je h 0,951 0243
dodécaèdre tronqué t{5,3}
Nœud CDel 1.pngCDel 5.pngNœud CDel 1.pngCDel 3.pngCDel node.png 		Dodécaèdre tronqué   Cog-scripted-svg-blue.svg Polyèdre tronqué 12 max.png Polyèdre tronqué 12 net.svg 3.10.10
Polyèdre tronqué 12 vertfig.png 		32 20 triangles
12 décagones 		90 60 85,039 665 je h 0,926 0125
icosaèdre tronqué t{3,5}
Nœud CDel 1.pngCDel 3.pngNœud CDel 1.pngCDel 5.pngCDel node.png 		Icosaèdre tronqué   Cog-scripted-svg-blue.svg Polyèdre tronqué 20 max.png Polyèdre tronqué 20 net.svg 5.6.6
Polyèdre tronqué 20 vertfig.png 		32 12 pentagones
20 hexagones 		90 60 55,287 731 je h 0,966 6219
rhombicosidodécaèdre
(petit rhombicosidodécaèdre)		 rr{5,3}
Nœud CDel 1.pngCDel 5.pngCDel node.pngCDel 3.pngNœud CDel 1.png 		Rhombicosidodécaèdre   Cog-scripted-svg-blue.svg Polyèdre petit losange 12-20 max.png Polyèdre petit losange 12-20 net.svg 3.4.5.4
Polyèdre petit losange 12-20 vertfig.png 		62 20 triangles
30 carrés
12 pentagones 		120 60 41,615 324 je h 0,979 2370
icosidodécaèdre tronqué
(grand rhombicosidodécaèdre)		 tr{5,3}
Nœud CDel 1.pngCDel 5.pngNœud CDel 1.pngCDel 3.pngNœud CDel 1.png 		Icosidodécaèdre tronqué   Cog-scripted-svg-blue.svg Polyèdre grand losange 12-20 max.png Polyèdre grand losange 12-20 net.svg 4.6.10
Polyèdre grand losange 12-20 vertfig light.png 		62 30 carrés
20 hexagones
12 décagones 		180 120 206.803 399 je h 0,970 3127
snub dodécaèdre
(snub icosidodécaèdre)		 sr{5,3}
Nœud CDel h.pngCDel 5.pngNœud CDel h.pngCDel 3.pngNœud CDel h.png 		Dodécaèdre snobé (Cw)   Cog-scripted-svg-blue.svg Polyèdre snub 12-20 gauche max.png Polyèdre snub 12-20 gauche net.svg 3.3.3.3.5
Polyèdre snub 12-20 gauche vertfig.png 		92 80 triangles
12 pentagones 		150 60 37.616 650 je 0,982 0114

Certaines définitions du polyèdre semi-régulier incluent une autre figure, la gyrobicupole carrée allongée ou "pseudo-rhombicuboctaèdre".

Propriétés

Le nombre de sommets est de 720° divisé par le défaut d'angle au sommet .

Le cuboctaèdre et l'icosidodécaèdre sont à bord uniforme et sont appelés quasi-réguliers .

Les duals des solides d'Archimède sont appelés les solides de Catalan . Avec les bipyramides et les trapézoèdres , ce sont les solides à faces uniformes avec des sommets réguliers.

Chiralité

Le cube snub et le dodécaèdre snub sont appelés chiraux , car ils se présentent sous une forme gaucher (latin : levomorph ou laevomorph) et droitier (latin : dextromorph). Quand quelque chose se présente sous plusieurs formes qui sont l' image miroir tridimensionnelle de l'autre , ces formes peuvent être appelées énantiomorphes. (Cette nomenclature est également utilisée pour les formes de certains composés chimiques .)

Construction des solides d'Archimède

Informations complémentaires : polyèdre uniforme et notation de polyèdre de Conway
Les solides d'Archimède peuvent être construits comme des positions génératrices dans un kaléidoscope .

Les différents solides d'Archimède et de Platon peuvent être liés les uns aux autres en utilisant une poignée de constructions générales. À partir d'un solide platonicien, la troncature consiste à couper des coins. Pour préserver la symétrie, la coupe est dans un plan perpendiculaire à la ligne joignant un coin au centre du polyèdre et est la même pour tous les coins. En fonction de la quantité tronquée (voir tableau ci-dessous), différents solides platoniciens et archimédiens (et autres) peuvent être créés. Si la troncature est suffisamment profonde pour que chaque paire de faces de sommets adjacents partage exactement un point, on parle de rectification. Une expansion , ou cantellation , consiste à éloigner chaque face du centre (de la même distance de manière à conserver la symétrie du solide platonicien) et à prendre l'enveloppe convexe. L'expansion avec torsion consiste également à faire pivoter les faces, divisant ainsi chaque rectangle correspondant à une arête en deux triangles par l'une des diagonales du rectangle. La dernière construction que nous utilisons ici est la troncature des coins et des bords. Ignorant la mise à l'échelle, l'expansion peut également être considérée comme la rectification de la rectification. De même, la cantitroncation peut être considérée comme la troncature de la rectification.

Construction des solides d'Archimède
Symétrie tétraédrique
Domaines de réflexion tétraédrique.png 		octaédrique
Domaines de réflexion octaédrique.png 		Icosaédrique
Domaines de réflexion icosaédriques.png
Démarrage solide
Opération		 Symbole
{p,q}
Nœud CDel 1.pngCDel p.pngCDel node.pngCDel q.pngCDel node.png 		Tétraèdre
{3,3}
Polyèdre uniforme-33-t0.png 		Cube
{4,3}
Polyèdre uniforme-43-t0.svg 		Octaèdre
{3,4}
Polyèdre uniforme-43-t2.svg 		dodécaèdre
{5,3}
Polyèdre uniforme-53-t0.svg 		Icosaèdre
{3,5}
Polyèdre uniforme-53-t2.svg
Troncation (t) t{p,q}
Nœud CDel 1.pngCDel p.pngNœud CDel 1.pngCDel q.pngCDel node.png 		tétraèdre tronqué
Polyèdre uniforme-33-t01.png 		cube tronqué
Polyèdre uniforme-43-t01.svg 		octaèdre tronqué
Polyèdre uniforme-43-t12.svg 		dodécaèdre tronqué
Polyèdre uniforme-53-t01.svg 		icosaèdre tronqué
Polyèdre uniforme-53-t12.svg
Rectification (r)
Ambo (a)		 r{p,q}
CDel node.pngCDel p.pngNœud CDel 1.pngCDel q.pngCDel node.png 		tétratétraèdre
(octaèdre)
Polyèdre uniforme-33-t1.png 		cuboctaèdre
Polyèdre uniforme-43-t1.svg 		icosidodécaèdre
Polyèdre uniforme-53-t1.svg
Bitruncation (2t)
Double kis (dk)		 2t{p,q}
CDel node.pngCDel p.pngNœud CDel 1.pngCDel q.pngNœud CDel 1.png 		tétraèdre tronqué
Polyèdre uniforme-33-t12.png 		octaèdre tronqué
Polyèdre uniforme-43-t12.png 		cube tronqué
Polyèdre uniforme-43-t01.svg 		icosaèdre tronqué
Polyèdre uniforme-53-t12.svg 		dodécaèdre tronqué
Polyèdre uniforme-53-t01.svg
Biectification (2r)
Double (d)		 2r{p,q}
CDel node.pngCDel p.pngCDel node.pngCDel q.pngNœud CDel 1.png 		tétraèdre
Polyèdre uniforme-33-t2.png 		octaèdre
Polyèdre uniforme-43-t2.svg 		cube
Polyèdre uniforme-43-t0.svg 		icosaèdre
Polyèdre uniforme-53-t2.svg 		dodécaèdre
Polyèdre uniforme-53-t0.svg
cantellation (rr)
Expansion (e)		 rr{p,q}
Nœud CDel 1.pngCDel p.pngCDel node.pngCDel q.pngNœud CDel 1.png 		rhombitetratétraèdre
(cuboctaèdre)
Polyèdre uniforme-33-t02.png 		rhombicuboctaèdre
Polyèdre uniforme-43-t02.png 		rhombicosidodécaèdre
Polyèdre uniforme-53-t02.png
Snub rectifié (sr)
Snub (s)		 sr{p,q}
Nœud CDel h.pngCDel p.pngNœud CDel h.pngCDel q.pngNœud CDel h.png 		snob tétratétraèdre
(icosaèdre)
Polyèdre uniforme-33-s012.svg 		snober le cuboctaèdre
Polyèdre uniforme-43-s012.png 		camoufler l'icosidodécaèdre
Polyèdre uniforme-53-s012.png
Cantitroncation (tr)
Biseau (b)		 tr{p,q}
Nœud CDel 1.pngCDel p.pngNœud CDel 1.pngCDel q.pngNœud CDel 1.png 		tétratétraèdre tronqué
(octaèdre tronqué)
Polyèdre uniforme-33-t012.png 		cuboctaèdre tronqué
Polyèdre uniforme-43-t012.png 		icosidodécaèdre tronqué
Polyèdre uniforme-53-t012.png

Notez la dualité entre le cube et l'octaèdre, et entre le dodécaèdre et l'icosaèdre. De plus, en partie parce que le tétraèdre est auto-duel, un seul solide d'Archimède a au plus une symétrie tétraédrique. (Tous les solides platoniciens ont au moins une symétrie tétraédrique, car la symétrie tétraédrique est une opération de symétrie des (c. être utilisé comme un tétraèdre amorti.)

Projection stéréographique

tétraèdre tronqué cube tronqué octaèdre tronqué dodécaèdre tronqué icosaèdre tronqué
Triangle de projection stéréographique en tétraèdre tronqué.png
triangle centré 		Projection stéréographique en tétraèdre tronqué hexagon.png
hexagone centré 		Projection stéréographique en cube tronqué octogone.png
octogone centré 		Triangle de projection stéréographique en cube tronqué.png
triangle centré 		Projection stéréographique octaèdre tronqué square.png
carré centré 		Projection stéréographique octaèdre tronqué hexagon.png
hexagone centré 		Projection stéréographique de dodécaèdre tronqué decagon.png
Décagone centré 		Triangle de projection stéréographique de dodécaèdre tronqué.png
Triangle centré 		Projection stéréographique d'icosaèdre tronqué pentagon.png
pentagone -centré 		Projection stéréographique d'icosaèdre tronqué hexagon.png
hexagone centré
cuboctaèdre icosidodécaèdre rhombicuboctaèdre rhombicosidodécaèdre
Cuboctaèdre projection stéréographique square.png
carré centré 		Triangle de projection stéréographique du cuboctaèdre.png
triangle centré 		Projection stéréographique du cuboctaèdre vertex.png
sommet -centré 		Icosidodécaèdre projection stéréographique pentagone.png
pentagone -centré 		Triangle de projection stéréographique icosidodécaèdre.png
triangle centré 		Place de projection stéréographique de rhombicuboctaèdre.png
carré centré 		Projection stéréographique rhombicuboctaèdre square2.png
carré centré 		Triangle de projection stéréographique du rhombicuboctaèdre.png
triangle centré 		Rhombicosidodécaèdre projection stéréographique pentagone'.png
Pentagone -centré 		Triangle de projection stéréographique rhombicosidodécaèdre.png
Triangle centré 		Place de projection stéréographique rhombicosidodécaèdre.png
Carré centré
cuboctaèdre tronqué icosidodécaèdre tronqué cube retroussé
Projection stéréographique cuboctaèdre tronqué square.png
carré centré 		Projection stéréographique cuboctaèdre tronqué hexagon.png
hexagone centré 		Projection stéréographique cuboctaèdre tronqué octagon.png
octogone centré 		Projection stéréographique d'icosidodécaèdre tronqué decagon.png Projection stéréographique d'icosidodécaèdre tronqué hexagon.png Projection stéréographique d'icosidodécaèdre tronqué square.png Snub cube projection stéréographique.png
carré centré

Voir également

Citations

Références générales

  • Grünbaum, Branko (2009), "Une erreur persistante", Elemente der Mathematik , 64 (3) : 89-101, doi : 10.4171/EM/120 , MR  2520469. Réimprimé dans Pitici, Mircea, éd. (2011), The Best Writing on Mathematics 2010 , Princeton University Press, pp. 18-31.
  • Jayatilake, Udaya (mars 2005). "Calculs sur les polyèdres réguliers de face et de sommet". Gazette mathématique . 89 (514) : 76-81. doi : 10.1017/S0025557200176818 . S2CID  125675814 ..
  • Malkevitch, Joseph (1988), « Jalons de l'histoire des polyèdres », in Senechal, M. ; Fleck, G. (eds.), Shaping Space: A Polyhedral Approach , Boston: Birkhäuser, pp. 80-92.
  • Pugh, Anthony (1976). Polyèdres : Une approche visuelle . Californie : University of California Press Berkeley. ISBN 0-520-03056-7. Chapitre 2
  • Williams, Robert (1979). La Fondation Géométrique de la Structure Naturelle : Un Livre Source de Conception . Dover Publications, Inc. ISBN 0-486-23729-X. (Section 3-9)
  • Schreiber, Pierre ; Fischer, Gisèle ; Sternath, Maria Louise (2008). « Nouvel éclairage sur la redécouverte des solides d'Archimède pendant la renaissance ». Archive pour l'histoire des sciences exactes . 62 (4) : 457-467. Bibcode : 2008AHES ... 62..457S . doi : 10.1007/s00407-008-0024-z . ISSN  0003-9519 . S2CID  122216140 ..

Liens externes