Polyèdre uniforme - Uniform polyhedron

Polyèdre en étoile uniforme : Dodécadodécaèdre Snub

Un polyèdre uniforme a des polygones réguliers comme faces et est vertex-transitif (c'est -à- dire qu'il existe une isométrie mappant n'importe quel sommet sur n'importe quel autre). Il s'ensuit que tous les sommets sont congrus .

Les polyèdres uniformes peuvent être réguliers (si aussi face et arête transitifs), quasi-réguliers (si aussi arête transitive mais pas face transitive), ou semi-réguliers (si ni arête ni face transitive). Les faces et les sommets n'ont pas besoin d'être convexes , donc beaucoup de polyèdres uniformes sont aussi des polyèdres en étoile .

Il existe deux classes infinies de polyèdres uniformes, ainsi que 75 autres polyèdres :

Classes infinies :
- prismes ,
- antiprismes .
Convexe exceptionnel :
- 5 Solides platoniciens : polyèdres convexes réguliers,
- 13 solides d'Archimède : 2 polyèdres quasi - réguliers et 11 semi-réguliers convexes.
Etoile (non convexe) exceptionnelle :
- 4 Polyèdres de Kepler–Poinsot : polyèdres réguliers non convexes,
- 53 polyèdres étoilés uniformes : 5 quasiréguliers et 48 semiréguliers.

D'où 5 + 13 + 4 + 53 = 75.

Il existe également de nombreux polyèdres uniformes dégénérés avec des paires d'arêtes qui coïncident, dont l'un trouvé par John Skilling appelé le grand dirhombidodecaèdre disnub (figure de Skilling).

Les polyèdres doubles aux polyèdres uniformes sont face-transitifs (isoédriques) et ont des figures de sommet régulières , et sont généralement classés en parallèle avec leur polyèdre double (uniforme). Le dual d'un polyèdre régulier est régulier, tandis que le dual d'un solide d'Archimède est un solide de Catalan .

Le concept de polyèdre uniforme est un cas particulier du concept de polytope uniforme , qui s'applique également aux formes dans l'espace de dimension supérieure (ou de dimension inférieure).

Définition

Le Péché Originel dans la théorie des polyèdres remonte à Euclide, et à travers Kepler, Poinsot, Cauchy et bien d'autres continue d'affliger tous les travaux sur ce sujet (y compris celui du présent auteur). Elle vient du fait que l'usage traditionnel du terme « polyèdres réguliers » était, et est, contraire à la syntaxe et à la logique : les mots semblent impliquer qu'il s'agit, parmi les objets que nous appelons « polyèdres », de ces objets spéciaux. celles qui méritent d'être qualifiées de « régulières ». Mais à chaque étape — Euclide, Kepler, Poinsot, Hess, Brückner,…— les auteurs n'ont pas réussi à définir quels sont les « polyèdres » parmi lesquels ils trouvent les « réguliers ».

(Branko Grünbaum 1994 )

Coxeter, Longuet-Higgins & Miller (1954) définissent les polyèdres uniformes comme étant des polyèdres vertex-transitifs à faces régulières. Ils définissent un polyèdre comme un ensemble fini de polygones tel que chaque côté d'un polygone est un côté d'un seul autre polygone, de sorte qu'aucun sous-ensemble propre non vide des polygones n'a la même propriété. Par polygone, ils désignent implicitement un polygone dans l'espace euclidien à trois dimensions ; ceux-ci sont autorisés à être non convexes et à se croiser.

Il existe quelques généralisations du concept de polyèdre uniforme. Si l'hypothèse de connexité est abandonnée, nous obtenons des composés uniformes, qui peuvent être divisés en une union de polyèdres, tels que le composé de 5 cubes. Si l'on laisse tomber la condition que la réalisation du polyèdre soit non dégénérée, alors on obtient ce que l'on appelle les polyèdres uniformes dégénérés. Ceux-ci nécessitent une définition plus générale des polyèdres. Grünbaum (1994) a donné une définition assez compliquée d'un polyèdre, tandis que McMullen & Schulte (2002) ont donné une définition plus simple et plus générale d'un polyèdre : dans leur terminologie, un polyèdre est un polytope abstrait à 2 dimensions avec un 3 non dégénéré. -réalisation dimensionnelle. Ici, un polytope abstrait est un ensemble de ses "faces" satisfaisant diverses conditions, une réalisation est une fonction de ses sommets à un certain espace, et la réalisation est dite non dégénérée si deux faces distinctes du polytope abstrait ont des réalisations distinctes. Certaines des façons dont ils peuvent être dégénérés sont les suivantes:

Visages cachés. Certains polyèdres ont des faces cachées, en ce sens qu'aucun point de leur intérieur n'est visible de l'extérieur. Ceux-ci ne sont généralement pas comptés comme des polyèdres uniformes.
Composés dégénérés. Certains polyèdres ont plusieurs arêtes et leurs faces sont les faces de deux ou plusieurs polyèdres, bien que ce ne soient pas des composés au sens précédent puisque les polyèdres partagent des arêtes.
Doubles couvertures. Il existe des polyèdres non orientables qui ont des doubles couvertures satisfaisant la définition d'un polyèdre uniforme. Là, les doubles couvertures ont des faces, des arêtes et des sommets doublés. Ils ne sont généralement pas comptés comme des polyèdres uniformes.
Doubles visages. Il existe plusieurs polyèdres à faces doublées produits par la construction de Wythoff. La plupart des auteurs n'autorisent pas les faces doublées et les suppriment dans le cadre de la construction.
Bords doubles. La figure de Skilling a la propriété d'avoir des arêtes doubles (comme dans les polyèdres uniformes dégénérés) mais ses faces ne peuvent pas être écrites comme une union de deux polyèdres uniformes.

Histoire

Polyèdres convexes réguliers

Les solides platoniciens retour date aux Grecs classiques et ont été étudiés par les pythagoriciens , Platon (c 424 -. 348 BC), Théétète (c 417 BC -. 369 BC), Timée de Locri (vers 420-380 avant JC) et Euclide (fl. 300 av. J.-C.). Les Étrusques ont découvert le dodécaèdre régulier avant 500 av.

Polyèdres convexes uniformes non réguliers

Le cuboctaèdre était connu de Platon .
Archimède (287 av. J.-C. - 212 av. J.-C.) a découvert l'ensemble des 13 solides d'Archimède . Son livre original sur le sujet a été perdu, mais Pappus d'Alexandrie (c. 290 - c. 350 après JC) a mentionné qu'Archimède a répertorié 13 polyèdres.
Piero della Francesca (1415 – 1492) a redécouvert les cinq troncatures des solides platoniciens : tétraèdre tronqué, octaèdre tronqué, cube tronqué, dodécaèdre tronqué et icosaèdre tronqué, et a inclus des illustrations et des calculs de leurs propriétés métriques dans son livre De quinquebus corporibus . Il a également discuté du cuboctaèdre dans un autre livre.
Luca Pacioli a plagié le travail de Francesca dans De divina proportione en 1509, ajoutant le rhombicuboctaèdre , l'appelant un icosihexaèdre pour ses 26 faces, qui a été dessiné par Léonard de Vinci .
Johannes Kepler (1571-1630) fut le premier à publier la liste complète des solides d'Archimède , en 1619, ainsi qu'à identifier les familles infinies de prismes et antiprismes uniformes .

Polyèdres étoilés réguliers

Kepler (1619) a découvert deux des polyèdres réguliers de Kepler-Poinsot et Louis Poinsot (1809) a découvert les deux autres. L'ensemble de quatre a été prouvé complet par Augustin Cauchy (1789 - 1857) et nommé par Arthur Cayley (1821 - 1895).

Autres 53 polyèdres étoilés non réguliers

Sur les 53 restants, Edmund Hess (1878) en a découvert deux, Albert Badoureau (1881) en a découvert 36 autres et Pitsch (1881) en a découvert indépendamment 18, dont 3 n'avaient pas été découverts auparavant. Ensemble, ils ont donné 41 polyèdres.
Le géomètre HSM Coxeter a découvert les douze autres en collaboration avec JCP Miller (1930-1932) mais n'a pas publié. MS Longuet-Higgins et HC Longuet-Higgins en ont indépendamment découvert onze. Lesavre et Mercier en ont redécouvert cinq en 1947.
Coxeter, Longuet-Higgins & Miller (1954) ont publié la liste des polyèdres uniformes.
Sopov (1970) a prouvé sa conjecture que la liste était complète.
En 1974, Magnus Wenninger a publié son livre Modèles de polyèdres , qui répertorie les 75 polyèdres uniformes non prismatiques, avec de nombreux noms inédits qui leur ont été donnés par Norman Johnson .
Skilling (1975) a prouvé indépendamment l'exhaustivité et a montré que si la définition du polyèdre uniforme est assouplie pour permettre aux arêtes de coïncider, il n'y a qu'une seule possibilité supplémentaire.
En 1987, Edmond Bonan a dessiné tous les polyèdres uniformes et leurs duels en 3D, avec un programme Turbo Pascal appelé Polyca : la quasi- totalité d'entre eux ont été montrés lors du Congrès de l'Union Stéréoscopique Internationale qui s'est tenu au Congress Theatre, Eastbourne, Royaume-Uni.
En 1993, Zvi Har'El a produit une construction kaléidoscopique complète des polyèdres uniformes et des duels avec un programme informatique appelé Kaleido , et résumé dans un document Uniform Solution for Uniform Polyhedra , en comptant les chiffres 1-80.
Toujours en 1993, R. Mäder a porté cette solution Kaleido sur Mathematica avec un système d'indexation légèrement différent.
En 2002, Peter W. Messer a découvert un ensemble minimal d'expressions fermées pour déterminer les principales quantités combinatoires et métriques de tout polyèdre uniforme (et son dual) étant donné seulement son symbole de Wythoff .

Polyèdres étoilés uniformes

Le grand dirhombicosidodécaèdre, le seul polyèdre uniforme non wythoffien

Les 57 formes non prismatiques non convexes, à l'exception du grand dirhombicosidodécaèdre , sont compilées par des constructions de Wythoff dans les triangles de Schwarz .

Formes convexes par construction Wythoff

Les polyèdres uniformes convexes peuvent être nommés par des opérations de construction de Wythoff sur la forme régulière.

Plus en détail, les polyèdres uniformes convexes sont donnés ci-dessous par leur construction de Wythoff au sein de chaque groupe de symétrie.

Dans la construction de Wythoff, il y a des répétitions créées par des formes de symétrie inférieure. Le cube est un polyèdre régulier et un prisme carré. L' octaèdre est un polyèdre régulier et un antiprisme triangulaire. L' octaèdre est aussi un tétraèdre rectifié . De nombreux polyèdres sont répétés à partir de différentes sources de construction et sont colorés différemment.

La construction de Wythoff s'applique également aux polyèdres uniformes et aux pavages uniformes sur la surface d'une sphère , de sorte que des images des deux sont données. Les pavages sphériques comprenant l'ensemble des hoèdres et dièdres qui sont des polyèdres dégénérés.

Ces groupes de symétrie sont formés à partir des groupes de points de réflexion en trois dimensions , chacun représenté par un triangle fondamental ( p q r ), où p > 1, q > 1, r > 1 et 1/ p + 1/ q + 1/ r < 1 .

Symétrie tétraédrique (3 3 2) – ordre 24
Symétrie octaédrique (4 3 2) – ordre 48
Symétrie icosaédrique (5 3 2) – ordre 120
Symétrie dièdre ( n 2 2), pour n = 3,4,5,... – ordre 4 n

Les formes non réfléchissantes restantes sont construites par des opérations d' alternance appliquées aux polyèdres à nombre pair de côtés.

Aux prismes et à leur symétrie dièdre , le processus de construction sphérique de Wythoff ajoute deux classes régulières qui deviennent dégénérées en polyèdres : les dièdres et les hosohèdres , le premier n'ayant que deux faces, et le second seulement deux sommets. La troncature des hosohèdres réguliers crée les prismes.

Au-dessous des polyèdres uniformes convexes sont indexés de 1 à 18 pour les formes non prismatiques telles qu'elles sont présentées dans les tableaux par forme de symétrie.

Pour l'ensemble infini des formes prismatiques, elles sont répertoriées en quatre familles :

Hosohedra H _2... (uniquement en pavage sphérique)
Dihedra D _2... (uniquement en pavage sphérique)
Prismes P _3... (hosohèdres tronqués)
Antiprismes A _3... (prismes retroussés)

Tableaux récapitulatifs

Nom de Johnson	Parent	Tronqué	Rectifié	Bitroncé (tr. dual)	Birectifié (double)	Cantellé	Omnitronqué ( cantitronqué )	Snober
Diagramme de Coxeter
Symbole Schläfli étendu	${\begin{Bmatrix}p,q\end{Bmatrix}}$	$t{\begin{Bmatrix}p,q\end{Bmatrix}}$	${\begin{Bmatrix}p\\q\end{Bmatrix}}$	$t{\begin{Bmatrix}q,p\end{Bmatrix}}$	${\begin{Bmatrix}q,p\end{Bmatrix}}$	$r{\begin{Bmatrix}p\\q\end{Bmatrix}}$	$t{\begin{Bmatrix}p\\q\end{Bmatrix}}$	$s{\begin{Bmatrix}p\\q\end{Bmatrix}}$
	{p,q}	t{p,q}	r{p,q}	2t{p,q}	2r{p,q}	rr{p,q}	tr{p,q}	sr{p,q}
	t ₀ {p,q}	t _0,1 {p,q}	t ₁ {p,q}	t _1,2 {p,q}	t ₂ {p,q}	t _0,2 {p,q}	t _0,1,2 {p,q}	ht _0,1,2 {p,q}
Symbole Wythoff (pq 2)	q \| p 2	2 q \| p	2 \| pq	2 p \| q	p \| q 2	pq \| 2	pq 2 \|	\| pq 2
Figure de sommet	p ^q	q.2p.2p	(pq) ²	p.2q.2q	q ^p	p.4.q.4	4.2p.2q	3.3.p.3.q
Tétraédrique (3 3 2)	3.3.3	3.6.6	3.3.3.3	3.6.6	3.3.3	3.4.3.4	4.6.6	3.3.3.3.3
Octaédrique (4 3 2)	4.4.4	3.8.8	3.4.3.4	4.6.6	3.3.3.3	3.4.4.4	4.6.8	3.3.3.3.4
Icosaédrique (5 3 2)	5.5.5	3.10.10	3.5.3.5	5.6.6	3.3.3.3.3	3.4.5.4	4.6.10	3.3.3.3.5

Et un échantillon de symétries dièdres :

(La sphère n'est pas coupée, seul le pavage est coupé.) (Sur une sphère, une arête est l'arc du grand cercle, le chemin le plus court, entre ses deux sommets. Par conséquent, un digon dont les sommets ne sont pas polaires-opposés est plat : on dirait un bord.)

(p 2 2)	Parent	Tronqué	Rectifié	Bitroncé (tr. dual)	Birectifié (double)	Cantellé	Omnitronqué ( cantitronqué )	Snober
Diagramme de Coxeter
Symbole Schläfli étendu	${\begin{Bmatrix}p,2\end{Bmatrix}}$	$t{\begin{Bmatrix}p,2\end{Bmatrix}}$	${\begin{Bmatrix}p\\2\end{Bmatrix}}$	$t{\begin{Bmatrix}2,p\end{Bmatrix}}$	${\begin{Bmatrix}2,p\end{Bmatrix}}$	$r{\begin{Bmatrix}p\\2\end{Bmatrix}}$	$t{\begin{Bmatrix}p\\2\end{Bmatrix}}$	$s{\begin{Bmatrix}p\\2\end{Bmatrix}}$
	{p,2}	t{p,2}	r{p,2}	2t{p,2}	2r{p,2}	rr{p,2}	tr{p,2}	sr{p,2}
	t ₀ {p,2}	t _0,1 {p,2}	t ₁ {p,2}	t _1,2 {p,2}	t ₂ {p,2}	t _0,2 {p,2}	t _0,1,2 {p,2}	ht _0,1,2 {p,2}
Symbole Wythoff	2 \| p 2	2 2 \| p	2 \| p 2	2 p \| 2	p \| 2 2	p 2 \| 2	p 2 2 \|	\| p 2 2
Figure de sommet	p ²	2.2p.2p	p.2.p.2	p.4.4	2 ^p	p.4.2.4	4.2p.4	3.3.3.p
Dièdre (2 2 2)	{2,2}	2.4.4	2.2.2.2	4.4.2	2.2	2.4.2.4	4.4.4	3.3.3.2
Dièdre (3 2 2)	3.3	2.6.6	2.3.2.3	4.4.3	2.2.2	2.4.3.4	4.4.6	3.3.3.3
Dièdre (4 2 2)	4.4	2.8.8	2.4.2.4	4.4.4	2.2.2.2	2.4.4.4	4.4.8	3.3.3.4
Dièdre (5 2 2)	5.5	2.10.10	2.5.2.5	4.4.5	2.2.2.2.2	2.4.5.4	4.4.10	3.3.3.5
Dièdre (6 2 2)	6.6	2.12.12	2.6.2.6	4.4.6	2.2.2.2.2.2	2.4.6.4	4.4.12	3.3.3.6

(3 3 2) T _d symétrie tétraédrique

La symétrie tétraédrique de la sphère génère 5 polyèdres uniformes, et une 6ème forme par une opération d'amortissement.

La symétrie tétraédrique est représentée par un triangle fondamental à un sommet avec deux miroirs, et deux sommets avec trois miroirs, représentés par le symbole (3 3 2). Il peut aussi être représenté par le groupe de Coxeter A ₂ ou [3,3], ainsi qu'un diagramme de Coxeter :.

Il y a 24 triangles, visibles dans les faces de l' hexaèdre tétrakis , et dans les triangles alternativement colorés sur une sphère :

#	Nom	Graphique A ₃	Graphique A ₂	Photo	Carrelage	Figure de sommet	Symboles de Coxeter et Schläfli	Nombre de visages par position			Nombre d'éléments
#	Nom	Graphique A ₃	Graphique A ₂	Photo	Carrelage	Figure de sommet	Symboles de Coxeter et Schläfli	Pos. 2 [3] (4)	Pos. 1 [2] (6)	Pos. 0 [3] (4)	Visages	Bords	Sommets
1	Tétraèdre						{3,3}	{3}			4	6	4
[1]	Tétraèdre birectifé (identique au tétraèdre )						t ₂ {3,3}={3,3}			{3}	4	6	4
2	Tétraèdre rectifié Tétratétraèdre (identique à l' octaèdre )						t ₁ {3,3}=r{3,3}	{3}		{3}	8	12	6
3	Tétraèdre tronqué						t _0,1 {3,3}=t{3,3}	{6}		{3}	8	18	12
[3]	Tétraèdre tronqué (identique au tétraèdre tronqué )						t _1,2 {3,3}=t{3,3}	{3}		{6}	8	18	12
4	Tétraèdre cantellé Rhombitetratetraèdre (identique au cuboctaèdre )						t _0,2 {3,3}=rr{3,3}	{3}	{4}	{3}	14	24	12
5	Omnitruncated tétraèdre tronqué tetratetrahedron (comme tronqué octaèdre )						t _0,1,2 {3,3}=tr{3,3}	{6}	{4}	{6}	14	36	24
6	Snub tétratétraèdre (identique à l' icosaèdre )						sr{3,3}	{3}	2 {3}	{3}	20	30	12

(4 3 2) O _h symétrie octaédrique

La symétrie octaédrique de la sphère génère 7 polyèdres uniformes, et un 7 de plus par alternance. Six de ces formes sont répétées à partir du tableau de symétrie tétraédrique ci-dessus.

La symétrie octaédrique est représentée par un triangle fondamental (4 3 2) comptant les miroirs à chaque sommet. Il peut aussi être représenté par le groupe de Coxeter B ₂ ou [4,3], ainsi qu'un diagramme de Coxeter :.

Il y a 48 triangles, visibles dans les faces du dodécaèdre disdyakis , et dans les triangles alternativement colorés sur une sphère :

#	Nom	Graphique B ₃	Graphique B ₂	Photo	Carrelage	Figure de sommet	Symboles de Coxeter et Schläfli	Nombre de visages par position			Nombre d'éléments
#	Nom	Graphique B ₃	Graphique B ₂	Photo	Carrelage	Figure de sommet	Symboles de Coxeter et Schläfli	Pos. 2 [4] (6)	Pos. 1 [2] (12)	Pos. 0 [3] (8)	Visages	Bords	Sommets
7	cube						{4,3}	{4}			6	12	8
[2]	Octaèdre						{3,4}			{3}	8	12	6
[4]	Cube Rectifié Rectifié octaèdre ( Cuboctaèdre )						{4,3}	{4}		{3}	14	24	12
8	Cube tronqué						t _0,1 {4,3}=t{4,3}	{8}		{3}	14	36	24
[5]	Octaèdre tronqué						t _0,1 {3,4}=t{3,4}	{4}		{6}	14	36	24
9	Cube cantellé Octaèdre cantellé Rhombicuboctaèdre						t _0,2 {4,3}=rr{4,3}	{4}	{4}	{3}	26	48	24
dix	Cube omnitronqué Octaèdre omnitronqué Cuboctaèdre tronqué						t _0,1,2 {4,3}=tr{4,3}	{8}	{4}	{6}	26	72	48
[6]	Octaèdre snobé (identique à l' icosaèdre )						= s{3,4}=sr{3,3}		{3}	{3}	20	30	12
[1]	Demi cube (identique au tétraèdre )						= h{4,3}={3,3}	¹ / ₂ {3}			4	6	4
[2]	Cube cantic (identique au tétraèdre tronqué )						= h ₂ {4,3}=t{3,3}	¹ / ₂ {6}		¹ / ₂ {3}	8	18	12
[4]	(identique au cuboctaèdre )						= rr{3,3}				14	24	12
[5]	(identique à l' octaèdre tronqué )						= tr{3,3}				14	36	24
[9]	Cantic snub octaèdre (identique au rhombicuboctaèdre )						s ₂ {3,4}=rr{3,4}				26	48	24
11	Snob cuboctaèdre						sr{4,3}	{4}	2 {3}	{3}	38	60	24

(5 3 2) I _h symétrie icosaédrique

La symétrie icosaédrique de la sphère génère 7 polyèdres uniformes, et un 1 de plus par alternance. Un seul est répété à partir du tableau de symétrie tétraédrique et octaédrique ci-dessus.

La symétrie icosaédrique est représentée par un triangle fondamental (5 3 2) comptant les miroirs à chaque sommet. Il peut aussi être représenté par le groupe de Coxeter G ₂ ou [5,3], ainsi qu'un diagramme de Coxeter :.

Il y a 120 triangles, visibles dans les faces du triacontaèdre disdyakis , et dans les triangles alternativement colorés sur une sphère :

#	Nom	Graphique (A ₂ ) [6]	Graphique (H ₃ ) [10]	Photo	Carrelage	Figure de sommet	Symboles de Coxeter et Schläfli	Nombre de visages par position			Nombre d'éléments
#	Nom	Graphique (A ₂ ) [6]	Graphique (H ₃ ) [10]	Photo	Carrelage	Figure de sommet	Symboles de Coxeter et Schläfli	Pos. 2 [5] (12)	Pos. 1 [2] (30)	Pos. 0 [3] (20)	Visages	Bords	Sommets
12	Dodécaèdre						{5,3}	{5}			12	30	20
[6]	Icosaèdre						{3,5}			{3}	20	30	12
13	dodécaèdre rectifié icosaèdre rectifié Icosidodécaèdre						t ₁ {5,3}=r{5,3}	{5}		{3}	32	60	30
14	dodécaèdre tronqué						t _0,1 {5,3}=t{5,3}	{dix}		{3}	32	90	60
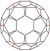
15	Icosaèdre tronqué						t _0,1 {3,5}=t{3,5}	{5}		{6}	32	90	60
16	Dodécaèdre cantellé Icosaèdre cantellé Rhombicosidodécaèdre						t _0,2 {5,3}=rr{5,3}	{5}	{4}	{3}	62	120	60
17	Omnitruncated dodécaèdre Omnitruncated icosaèdre tronqué icosidodécaèdre						t _0,1,2 {5,3}=tr{5,3}	{dix}	{4}	{6}	62	180	120
18	Icosidodécaèdre snob						sr{5,3}	{5}	2 {3}	{3}	92	150	60

(p 2 2) Prismatique [p,2], I ₂ (p) famille (D _{p h} dièdre symétrie)

La symétrie dièdre de la sphère génère deux ensembles infinis de polyèdres uniformes, prismes et antiprismes, et deux autres ensembles infinis de polyèdres dégénérés, les hosohèdres et dièdres qui existent sous forme de pavages sur la sphère.

La symétrie dièdre est représentée par un triangle fondamental (p 2 2) comptant les miroirs à chaque sommet. Il peut aussi être représenté par le groupe de Coxeter I ₂ (p) ou [n,2], ainsi qu'un diagramme de Coxeter prismatique :.

Ci-dessous se trouvent les cinq premières symétries dièdres : D ₂ ... D ₆ . La symétrie dièdre D _p a l'ordre 4n , représente les faces d'une bipyramide , et sur la sphère comme une ligne d'équateur sur la longitude, et n lignes de longitude équidistantes.

(2 2 2) Symétrie dièdre

Il y a 8 triangles fondamentaux, visibles sur les faces de la bipyramide carrée (Octaèdre) et des triangles alternativement colorés sur une sphère :

#	Nom	Photo	Carrelage	Figure de sommet	Symboles de Coxeter et Schläfli	Nombre de visages par position			Nombre d'éléments
#	Nom	Photo	Carrelage	Figure de sommet	Symboles de Coxeter et Schläfli	Pos. 2 [2] (2)	Pos. 1 [2] (2)	Pos. 0 [2] (2)	Visages	Bords	Sommets
D ₂ H ₂	Digonal dièdre , digonal hosohedron				{2,2}	{2}			2	2	2
J ₄	Dièdre digone tronqué (identique au dièdre carré )				t{2,2}={4,2}	{4}			2	4	4
P ₄ [7]	Dièdre digonal omnitronqué (identique au cube )				t _0,1,2 {2,2}=tr{2,2}	{4}	{4}	{4}	6	12	8
Un ₂ [1]	Dièdre digonal retroussé (identique au tétraèdre )				sr{2,2}		2 {3}		4	6	4

(3 2 2) D _3h symétrie dièdre

Il y a 12 triangles fondamentaux, visibles sur les faces de la bipyramide hexagonale et des triangles alternativement colorés sur une sphère :

#	Nom	Photo	Carrelage	Figure de sommet	Symboles de Coxeter et Schläfli	Nombre de visages par position			Nombre d'éléments
#	Nom	Photo	Carrelage	Figure de sommet	Symboles de Coxeter et Schläfli	Pos. 2 [3] (2)	Pos. 1 [2] (3)	Pos. 0 [2] (3)	Visages	Bords	Sommets
D ₃	Dièdre trigonal				{3,2}	{3}			2	3	3
H ₃	Hosèdre trigonal				{2,3}			{2}	3	3	2
D ₆	Dièdre trigonal tronqué (identique au dièdre hexagonal )				t{3,2}	{6}			2	6	6
P ₃	Hosohèdre trigonal tronqué ( Prisme triangulaire )				t{2,3}	{3}	{4}		5	9	6
P ₆	Dièdre trigonal omnitronqué ( Prisme hexagonal )				t _0,1,2 {2,3}=tr{2,3}	{6}	{4}	{4}	8	18	12
Un ₃ [2]	Dièdre trigonal retroussé (identique à l' antiprisme triangulaire ) (identique à l' octaèdre )				sr{2,3}	{3}	2 {3}		8	12	6
P ₃	Dièdre trigonal snub Cantic ( Prisme triangulaire )				s ₂ {2,3}=t{2,3}				5	9	6

(4 2 2) D _4h symétrie dièdre

Il y a 16 triangles fondamentaux, visibles sur les faces de la bipyramide octogonale et des triangles alternativement colorés sur une sphère :

#	Nom	Photo	Carrelage	Figure de sommet	Symboles de Coxeter et Schläfli	Nombre de visages par position			Nombre d'éléments
#	Nom	Photo	Carrelage	Figure de sommet	Symboles de Coxeter et Schläfli	Pos. 2 [4] (2)	Pos. 1 [2] (4)	Pos. 0 [2] (4)	Visages	Bords	Sommets
J ₄	dièdre carré				{4,2}	{4}			2	4	4
H ₄	hosèdre carré				{2,4}			{2}	4	4	2
J ₈	Dièdre carré tronqué (identique au dièdre octogonal )				t{4,2}	{8}			2	8	8
P ₄ [7]	Hosèdre carré tronqué ( Cube )				t{2,4}	{4}	{4}		6	12	8
J ₈	Dièdre carré omnitronqué ( Prisme octogonal )				t _0,1,2 {2,4}=tr{2,4}	{8}	{4}	{4}	dix	24	16
Un ₄	Dièdre carré retroussé ( Antiprisme carré )				sr{2,4}	{4}	2 {3}		dix	16	8
P ₄ [7]	Dièdre carré snub Cantic ( Cube )				s ₂ {4,2}=t{2,4}				6	12	8
Un ₂ [1]	Hosohèdre carré retroussé ( Antiprisme Digonal ) ( Tétraèdre )				s{2,4}=sr{2,2}				4	6	4

(5 2 2) D _5h symétrie dièdre

Il y a 20 triangles fondamentaux, visibles sur les faces de la bipyramide décagonale et des triangles alternativement colorés sur une sphère :

#	Nom	Photo	Carrelage	Figure de sommet	Symboles de Coxeter et Schläfli	Nombre de visages par position			Nombre d'éléments
#	Nom	Photo	Carrelage	Figure de sommet	Symboles de Coxeter et Schläfli	Pos. 2 [5] (2)	Pos. 1 [2] (5)	Pos. 0 [2] (5)	Visages	Bords	Sommets
D ₅	Dièdre pentagonal				{5,2}	{5}			2	5	5
H ₅	Hosèdre pentagonal				{2,5}			{2}	5	5	2
D ₁₀	Dièdre pentagonal tronqué (identique au dièdre décagonal )				t{5,2}	{dix}			2	dix	dix
P ₅	Hosohèdre pentagonal tronqué (identique au prisme pentagonal )				t{2,5}	{5}	{4}		7	15	dix
P ₁₀	Dièdre pentagonal omnitronqué ( Prisme décagonal )				t _0,1,2 {2,5}=tr{2,5}	{dix}	{4}	{4}	12	30	20
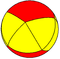
Un ₅	Camus pentagonal dièdre ( pentagonale antiprisme )				sr{2,5}	{5}	2 {3}		12	20	dix
P ₅	Dièdre pentagonal snub Cantic ( Prisme pentagonal )				s ₂ {5,2}=t{2,5}				7	15	dix

(6 2 2) D _6h symétrie dièdre

Il y a 24 triangles fondamentaux, visibles sur les faces de la bipyramide dodécagonale et des triangles alternativement colorés sur une sphère.

#	Nom	Photo	Carrelage	Figure de sommet	Symboles de Coxeter et Schläfli	Nombre de visages par position			Nombre d'éléments
#	Nom	Photo	Carrelage	Figure de sommet	Symboles de Coxeter et Schläfli	Pos. 2 [6] (2)	Pos. 1 [2] (6)	Pos. 0 [2] (6)	Visages	Bords	Sommets
D ₆	Dièdre hexagonal				{6,2}	{6}			2	6	6
H ₆	Hosèdre hexagonal				{2,6}			{2}	6	6	2
J ₁₂	Dièdre hexagonal tronqué (identique au dièdre dodécagonal )				t{6,2}	{12}			2	12	12
H ₆	Hosohèdre hexagonal tronqué (identique au prisme hexagonal )				t{2,6}	{6}	{4}		8	18	12
P ₁₂	Dièdre hexagonal omnitronqué ( Prisme dodécagonal )				t _0,1,2 {2,6}=tr{2,6}	{12}	{4}	{4}	14	36	24
Un ₆	Dièdre hexagonal retroussé ( Antiprisme hexagonal )				sr{2,6}	{6}	2 {3}		14	24	12
P ₃	Dièdre hexagonal cantique ( Prisme triangulaire )				= h ₂ {6,2}=t{2,3}				5	9	6
P ₆	Cantic snub dièdre hexagonal ( Prisme hexagonal )				s ₂ {6,2}=t{2,6}				8	18	12
Un ₃ [2]	Hosohèdre hexagonal retroussé (identique à l' antiprisme triangulaire ) (identique à l' octaèdre )				s{2,6}=sr{2,3}				8	12	6

Opérateurs de construction Wythoff

Opération	symbole	La description
Parent	{p,q} t ₀ {p,q}	Tout polyèdre régulier ou carrelage
Rectifié (r)	r{p,q} t ₁ {p,q}	Les bords sont entièrement tronqués en points uniques. Le polyèdre a maintenant les faces combinées du parent et du dual. Les polyèdres sont nommés par le nombre de côtés des deux formes régulières : {p,q} et {q,p}, comme le cuboctaèdre pour r{4,3} entre un cube et un octaèdre.
Birectifié (2r) (également double )	2r{p,q} t ₂ {p,q}	Le birectifié (dual) est une autre troncature afin que les faces originales soient réduites à des points. De nouvelles faces sont formées sous chaque sommet parent. Le nombre d'arêtes est inchangé et pivote de 90 degrés. Une birectification peut être vue comme le dual.
Tronqué (t)	t{p,q} t _0,1 {p,q}	Chaque sommet d'origine est coupé, avec une nouvelle face remplissant l'espace. La troncature a un degré de liberté, qui a une solution qui crée un polyèdre tronqué uniforme. Le polyèdre a ses faces d'origine doublées de côtés, et contient les faces du dual.
Bitroncé (2t) (également tronqué dual)	2t{p,q} t _1,2 {p,q}	Une bitruncation peut être vue comme la troncature du dual. Un cube tronqué est un octaèdre tronqué.
Cantellé (rr) (Également développé )	rr{p,q}	En plus de la troncature de sommet, chaque arête d'origine est biseautée avec de nouvelles faces rectangulaires apparaissant à leur place. Une cantellation uniforme est à mi-chemin entre la forme parentale et la forme duelle. Un polyèdre cantellé est nommé rhombi-r{p,q}, comme rhombicuboctaèdre pour rr{4,3}.
Cantitronqué (tr) (Aussi omnitronqué )	tr{p,q} t _0,1,2 {p,q}	Les opérations de troncature et de cantellation sont appliquées ensemble pour créer une forme omnitronquée qui a les faces du parent doublées sur les côtés, les faces du duel doublées sur les côtés et des carrés où les bords d'origine existaient.

Opérations d'alternance
Opération	symbole	La description
Snob rectifié (sr)	sr{p,q}	Le cantitronné alterné. Toutes les faces originales finissent par avoir deux fois moins de côtés, et les carrés dégénèrent en arêtes. Puisque les formes omnitronquées ont 3 faces/sommet, de nouveaux triangles se forment. Habituellement, ces formes à facettes alternées sont légèrement déformées par la suite afin de se terminer à nouveau par des polyèdres uniformes. La possibilité de cette dernière variation dépend du degré de liberté.
Snob (s)	s{p,2q}	Troncature alternée
Cantic snob (s ₂ )	s ₂ {p,2q}
Cantellation alternée (hrr)	hrr{2p,2q}	Uniquement possible en pavages uniformes (polyèdres infinis), alternance de Par exemple,
La moitié (h)	h{2p,q}	Alternance de, pareil que
Cantique (h ₂ )	h ₂ {2p,q}	Pareil que
Demi rectifié (h)	h{2p,2q}	Uniquement possible en pavages uniformes (polyèdres infinis), alternance de , pareil que ou Par exemple, = ou
Trimestre (q)	q{2p,2q}	Uniquement possible en pavages uniformes (polyèdres infinis), idem Par exemple, = ou

Voir également

Remarques

Les références

Brückner, M. Vielecke et vielflache. Théorie und geschichte. . Leipzig, Allemagne : Teubner, 1900. [2]
Coxeter, Harold Scott MacDonald ; Longuet-Higgins, MS ; Miller, JCP (1954). "Polyèdres uniformes" (PDF) . Transactions philosophiques de la Royal Society A . 246 (916) : 401–450. doi : 10.1098/rsta.1954.0003 . ISSN 0080-4614 . JSTOR 91532 . MR 0062446 .
Grünbaum, B. (1994), "Polyèdres aux visages creux", in Tibor Bisztriczky; Peter McMullen; Rolf Schneider ; et al. (éds.), Actes de l'Institut d'études avancées de l'OTAN sur les polytopes : abstrait, convexe et computationnel , Springer, pp. 43-70, doi : 10.1007/978-94-011-0924-6_3 , ISBN 978-94-010-4398-4
McMullen, Peter ; Schulte, Egon (2002), Abstract Regular Polytopes , Cambride University Press
Skilling, J. (1975). « L'ensemble complet des polyèdres uniformes ». Transactions philosophiques de la Royal Society de Londres. Série A. Sciences mathématiques et physiques . 278 (1278) : 111–135. doi : 10.1098/rsta.1975.0022 . ISSN 0080-4614 . JSTOR 74475 . MR 0365333 .
Sopov, SP (1970). « Une preuve de l'exhaustivité sur la liste des polyèdres homogènes élémentaires ». Ukrainskiui Geometricheskiui Sbornik (8) : 139-156. MR 0326550 .
Wenninger, Magnus (1974). Modèles de polyèdres . La presse de l'Universite de Cambridge. ISBN 978-0-521-09859-5.

Liens externes

Weisstein, Eric W. "Polyèdre uniforme" . MathWorld .
Solution uniforme pour les polyèdres uniformes
Les polyèdres uniformes
Polyèdres virtuels Polyèdres uniformes
Galerie de polyèdres uniformes
Polyèdre uniforme -- de Wolfram MathWorld A un graphique visuel de tous les 75

v t e Polytopes fondamentaux convexes réguliers et uniformes de dimensions 2 à 10
Famille	Un _n	B _n	I ₂ (p) / D _n	E ₆ / E ₇ / E ₈ / F ₄ / G ₂	H _n
Polygone régulier	Triangle	Carré	p-gon	Hexagone	Pentagone
Polyèdre uniforme	Tétraèdre	Octaèdre • Cube	demi-cube		Dodécaèdre • Icosaèdre
Polychore uniforme	Pentachoron	16 cellules • Tesseract	Demitesseract	24 cellules	120 cellules • 600 cellules
Uniforme 5-polytope	5-simplex	5 orthoplexes • 5 cubes	5-demicube
Uniforme 6-polytope	6-simplex	6-orthoplexe • 6-cube	6 demi-cube	1 ₂₂ • 2 ₂₁
Uniforme 7-polytope	7-simplex	7 orthoplexes • 7 cubes	7-demicube	1 ₃₂ • 2 ₃₁ • 3 ₂₁
Uniforme 8-polytope	8-simplex	8 orthoplexes • 8 cubes	8 demi-cube	1 ₄₂ • 2 ₄₁ • 4 ₂₁
Uniforme 9-polytope	9-simplex	9-orthoplexe • 9-cube	9 demi-cube
Uniforme 10-polytope	10-simplex	10 orthoplexes • 10 cubes	10-demicube
Uniforme n - polytope	n - simplexe	n - orthoplexe • n - cube	n - demi - cube	1 _k2 • 2 _k1 • k ₂₁	n - polytope pentagonal
Sujets: familles Polytope • polytope régulier • Liste des polyèdres réguliers et composés

Languages

In other projects

Polyèdre uniforme - Uniform polyhedron

Contenu

Définition

Histoire

Polyèdres convexes réguliers

Polyèdres convexes uniformes non réguliers

Polyèdres étoilés réguliers

Autres 53 polyèdres étoilés non réguliers

Polyèdres étoilés uniformes

Formes convexes par construction Wythoff

Tableaux récapitulatifs

(3 3 2) T _d symétrie tétraédrique

(4 3 2) O _h symétrie octaédrique

(5 3 2) I _h symétrie icosaédrique

(p 2 2) Prismatique [p,2], I ₂ (p) famille (D _{p h} dièdre symétrie)

(2 2 2) Symétrie dièdre

(3 2 2) D _3h symétrie dièdre

(4 2 2) D _4h symétrie dièdre

(5 2 2) D _5h symétrie dièdre

(6 2 2) D _6h symétrie dièdre

Opérateurs de construction Wythoff

Voir également

Remarques

Les références

Liens externes

Languages

In other projects

Polyèdre uniforme - Uniform polyhedron

Définition

Histoire

Polyèdres convexes réguliers

Polyèdres convexes uniformes non réguliers

Polyèdres étoilés réguliers

Autres 53 polyèdres étoilés non réguliers

Polyèdres étoilés uniformes

Formes convexes par construction Wythoff

Tableaux récapitulatifs

(3 3 2) T d symétrie tétraédrique

(4 3 2) O h symétrie octaédrique

(5 3 2) I h symétrie icosaédrique

(p 2 2) Prismatique [p,2], I 2 (p) famille (D p h dièdre symétrie)

(2 2 2) Symétrie dièdre

(3 2 2) D 3h symétrie dièdre

(4 2 2) D 4h symétrie dièdre

(5 2 2) D 5h symétrie dièdre

(6 2 2) D 6h symétrie dièdre

Opérateurs de construction Wythoff

Voir également

Remarques

Les références

Liens externes

(3 3 2) T _d symétrie tétraédrique

(4 3 2) O _h symétrie octaédrique

(5 3 2) I _h symétrie icosaédrique

(p 2 2) Prismatique [p,2], I ₂ (p) famille (D _{p h} dièdre symétrie)

(3 2 2) D _3h symétrie dièdre

(4 2 2) D _4h symétrie dièdre

(5 2 2) D _5h symétrie dièdre

(6 2 2) D _6h symétrie dièdre