Bialgèbre - Bialgebra

En mathématiques , une bialgèbre sur un corps K est un espace vectoriel sur K qui est à la fois une algèbre associative unitale et une gèbre charbonnière co- associative concomitante . Les structures algébriques et houillgébriques sont rendues compatibles avec quelques axiomes supplémentaires. Plus précisément, la comultiplication et le compte sont tous deux des homomorphismes d' algèbre unitale , ou de manière équivalente, la multiplication et l'unité de l'algèbre sont toutes deux des morphismes de la gèbre houillère . (Ces instructions sont équivalentes puisqu'elles sont exprimées par les mêmes diagrammes commutatifs .)

Des bialgèbres similaires sont liées par des homomorphismes de bialgèbre. Un homomorphisme de la bialgèbre est une carte linéaire qui est à la fois une algèbre et un homomorphisme de la gèbre houillère.

Comme en témoigne la symétrie des diagrammes commutatifs, la définition de la bialgèbre est auto-duelle , donc si l'on peut définir un dual de B (ce qui est toujours possible si B est de dimension finie), alors c'est automatiquement une bialgèbre.

Structures algébriques
Comme un groupe Grouper Semi-groupe  / Monoïde Rack et quandle Quasigroup et boucle Groupe abélien Magma Groupe de mensonge Théorie des groupes
anneau -comme Bague Rng Semiring Près de l'anneau Anneau commutatif Domaine intégral Domaine Anneau de division Théorie de l'anneau
Comme un treillis Treillis Demi-treillis Treillis complété Commande totale Algèbre de Heyting Algèbre de Boole Carte des treillis Théorie du treillis
Comme un module Module Regrouper avec les opérateurs Espace vectoriel Algèbre linéaire
Algèbre- like Algèbre Associatif Non associatif Algèbre de composition Algèbre de Lie Noté Bialgèbre
v t e

Définition formelle

( B , ∇, η, Δ, ε) est une bialgèbre sur K si elle a les propriétés suivantes:

• B est un espace vectoriel sur K ;
• il existe K - applications linéaires (multiplication) ∇: B ⊗ B → B (équivalent à K - application multilinéaire ∇: B × B → B ) et (unité) η: K → B , telles que ( B , ∇, η) est une associative unital algèbre ;
• il existe K les cartes de (comultiplication) Δ: B → B ⊗ B et (counité) ε: B → K , de telle sorte que ( B , Δ, ε) est un (counital coassociative) coalgèbre ;
• conditions de compatibilité exprimées par les schémas commutatifs suivants :

1. Multiplication ∇ et comultiplication Δ

   

   où τ: B ⊗ B → B ⊗ B est l'application linéaire définie par τ ( x ⊗ y ) = y ⊗ x pour tout x et y dans B ,

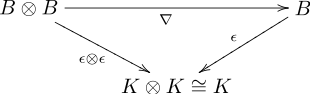
2. Multiplication ∇ et compte ε

   

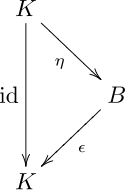
3. Comultiplication Δ et unité η

   

4. Unité η et compte ε

   

Coassociativité et conseil

L'application K- linéaire Δ: B → B ⊗ B est coassociative si . ${\ displaystyle (\ mathrm {id} _ {B} \ otimes \ Delta) \ circ \ Delta = (\ Delta \ otimes \ mathrm {id} _ {B}) \ circ \ Delta}$

L'application K- linéaire ε: B → K est un compte si . ${\ displaystyle (\ mathrm {id} _ {B} \ otimes \ epsilon) \ circ \ Delta = \ mathrm {id} _ {B} = (\ epsilon \ otimes \ mathrm {id} _ {B}) \ circ \ Delta}$

La coassociativité et le comptage sont exprimés par la commutativité des deux diagrammes suivants (ce sont les duaux des diagrammes exprimant l'associativité et l'unité d'une algèbre):

Conditions de compatibilité

Les quatre diagrammes commutatifs peuvent être lus soit comme "la comultiplication et le comptage sont des homomorphismes d'algèbres" ou, de manière équivalente, "la multiplication et l'unité sont des homomorphismes des gèbres charbonnières ".

Ces déclarations sont significatives une fois que nous expliquons les structures naturelles de l'algèbre et de la gèbre charbonnière dans tous les espaces vectoriels impliqués en plus de B : ( K , ∇ ₀ , η ₀ ) est une algèbre associative unitale de manière évidente et ( B ⊗ B , ∇ ₂ , η ₂ ) est une algèbre associative unitale avec unité et multiplication

${\ displaystyle \ eta _ {2}: = (\ eta \ otimes \ eta): K \ otimes K \ equiv K \ to (B \ otimes B)}$

${\ displaystyle \ nabla _ {2}: = (\ nabla \ otimes \ nabla) \ circ (id \ otimes \ tau \ otimes id) :( B \ otimes B) \ otimes (B \ otimes B) \ to (B \ otimes B)}$ ,

de sorte que ou, en omettant d' écrire et ∇ multiplication comme juxtaposition , ; ${\ displaystyle \ nabla _ {2} ((x_ {1} \ otimes x_ {2}) \ otimes (y_ {1} \ otimes y_ {2})) = \ nabla (x_ {1} \ otimes y_ {1 }) \ otimes \ nabla (x_ {2} \ otimes y_ {2})}$${\ displaystyle (x_ {1} \ otimes x_ {2}) (y_ {1} \ otimes y_ {2}) = x_ {1} y_ {1} \ otimes x_ {2} y_ {2}}$

de même, ( K , Δ ₀ , ε ₀ ) est une gèbre charbonnière de manière évidente et B ⊗ B est une gèbre charbonnière avec conseil et comultiplication

${\ displaystyle \ epsilon _ {2}: = (\ epsilon \ otimes \ epsilon) :( B \ otimes B) \ à K \ otimes K \ equiv K}$

${\ displaystyle \ Delta _ {2}: = (id \ otimes \ tau \ otimes id) \ circ (\ Delta \ otimes \ Delta) :( B \ otimes B) \ to (B \ otimes B) \ otimes (B \ otimes B)}$ .

Alors, les diagrammes 1 et 3 disent que Δ: B → B ⊗ B est un homomorphisme d'algèbres unitales (associatives) ( B , ∇, η) et ( B ⊗ B , ∇ ₂ , η ₂ )

${\ displaystyle \ Delta \ circ \ nabla = \ nabla _ {2} \ circ (\ Delta \ otimes \ Delta) :( B \ otimes B) \ to (B \ otimes B)}$ , ou simplement Δ ( xy ) = Δ ( x ) Δ ( y ),

${\ displaystyle \ Delta \ circ \ eta = \ eta _ {2}: K \ to (B \ otimes B)}$ , ou simplement Δ (1 _B ) = 1 _{B ⊗ B} ;

les diagrammes 2 et 4 disent que ε: B → K est un homomorphisme d'algèbres unitales (associatives) ( B , ∇, η) et ( K , ∇ ₀ , η ₀ ):

${\ displaystyle \ epsilon \ circ \ nabla = \ nabla _ {0} \ circ (\ epsilon \ otimes \ epsilon) :( B \ otimes B) \ à K}$ , ou simplement ε ( xy ) = ε ( x ) ε ( y )

${\ displaystyle \ epsilon \ circ \ eta = \ eta _ {0}: K \ à K}$ Ou simplement ε (1 _B ) = 1 _K .

De manière équivalente, les diagrammes 1 et 2 disent que ∇: B ⊗ B → B est un homomorphisme des gèbres charbonnières (coassociatives) ( B ⊗ B , Δ ₂ , ε ₂ ) et ( B , Δ, ε):

${\ displaystyle \ nabla \ otimes \ nabla \ circ \ Delta _ {2} = \ Delta \ circ \ nabla: (B \ otimes B) \ to (B \ otimes B),}$

${\ displaystyle \ nabla _ {0} \ circ \ epsilon _ {2} = \ epsilon \ circ \ nabla: (B \ otimes B) \ à K}$ ;

les diagrammes 3 et 4 disent que η: K → B est un homomorphisme des gèbres charbonneux (coassociatifs) ( K , Δ ₀ , ε ₀ ) et ( B , Δ, ε):

${\ displaystyle \ eta _ {2} \ circ \ Delta _ {0} = \ Delta \ circ \ eta: K \ to (B \ otimes B),}$

${\ displaystyle \ eta _ {0} \ circ \ epsilon _ {0} = \ epsilon \ circ \ eta: K \ à K}$ ,

où

${\ displaystyle \ epsilon _ {0} = \ epsilon \ circ \ eta}$ .

Exemples

Groupe bialgèbre

Un exemple de bialgèbre est l'ensemble des fonctions d'un groupe G (ou plus généralement de tout monoïde ) à , que nous pouvons représenter comme un espace vectoriel constitué de combinaisons linéaires de vecteurs de base standard e _g pour chaque g  ∈  G , qui peuvent représentent une distribution de probabilité sur G dans le cas de vecteurs dont les coefficients sont tous non négatifs et totalisent 1. Un exemple d'opérateurs de comultiplication et de comtés appropriés qui donnent une gèbre houillère de comté sont ${\ displaystyle \ mathbb {R}}$${\ displaystyle \ mathbb {R} ^ {G}}$

${\ displaystyle \ Delta (\ mathbf {e} _ {g}) = \ mathbf {e} _ {g} \ otimes \ mathbf {e} _ {g} \ ,,}$

qui représente faire une copie d'une variable aléatoire (que nous étendons à tous par linéarité), et ${\ displaystyle \ mathbb {R} ^ {G}}$

${\ displaystyle \ varepsilon (\ mathbf {e} _ {g}) = 1 \ ,,}$

(encore une fois étendu linéairement à tous ) qui représente le "traçage" d'une variable aléatoire - c'est -à- dire,  oublier la valeur d'une variable aléatoire (représentée par un seul facteur tenseur) pour obtenir une distribution marginale sur les variables restantes (les facteurs tensoriels restants) . Compte tenu de l'interprétation de (Δ, ε) en termes de distributions de probabilité comme ci-dessus, les conditions de cohérence de la bialgèbre se résument à des contraintes sur (∇, η) comme suit: ${\ displaystyle \ mathbb {R} ^ {G}}$

1. η est un opérateur préparant une distribution de probabilité normalisée indépendante de toutes les autres variables aléatoires;
2. Le produit ∇ mappe une distribution de probabilité sur deux variables à une distribution de probabilité sur une variable;
3. Copier une variable aléatoire dans la distribution donnée par η équivaut à avoir deux variables aléatoires indépendantes dans la distribution η;
4. Prendre le produit de deux variables aléatoires et préparer une copie de la variable aléatoire résultante a la même distribution que préparer des copies de chaque variable aléatoire indépendamment l'une de l'autre et les multiplier par paires.

Un couple (∇, η) qui satisfait ces contraintes est l' opérateur de convolution

${\ displaystyle \ nabla {\ bigl (} \ mathbf {e} _ {g} \ otimes \ mathbf {e} _ {h} {\ bigr)} = \ mathbf {e} _ {gh} \ ,,}$

de nouveau étendu à tous par linéarité; On obtient ainsi une distribution de probabilité normalisée à partir d' une répartition sur deux variables aléatoires, et présente une unité delta de distribution où i  ∈  G désigne l'élément d'identité du groupe G . ${\ displaystyle \ mathbb {R} ^ {G} \ otimes \ mathbb {R} ^ {G}}$${\ displaystyle \ eta = \ mathbf {e} _ {i} \ ;,}$

Autres exemples

D'autres exemples de bialgèbres comprennent l' algèbre tensorielle , qui peut être transformée en une bialgèbre en ajoutant la comultiplication et le conseil appropriés; ceux-ci sont élaborés en détail dans cet article.

Les bialgèbres peuvent souvent être étendues aux algèbres de Hopf , si un antipode approprié peut être trouvé. Ainsi, toutes les algèbres de Hopf sont des exemples de bialgèbres. Des structures similaires avec une compatibilité différente entre le produit et la comultiplication, ou différents types de multiplication et de comultiplication, comprennent les bialgèbres de Lie et les algèbres de Frobenius . Des exemples supplémentaires sont donnés dans l'article sur les houillères .

Voir également

• Quasi-bialgèbre

Remarques

Les références

• Dăscălescu, Sorin; Năstăsescu, Constantin; Raianu, Șerban (2001), Hopf Algebras: An introduction , Pure and Applied Mathematics, 235 (1ère éd.), Marcel Dekker, ISBN   0-8247-0481-9 .