Théorème fondamental de la théorie de Galois - Fundamental theorem of Galois theory

En mathématiques , le théorème fondamental de la théorie de Galois est un résultat qui décrit la structure de certains types d' extensions de champ en relation avec des groupes . Cela a été prouvé par Évariste Galois dans son développement de la théorie de Galois .

Dans sa forme la plus basique, le théorème affirme que , étant donné l'extension du champ E / F qui est finie et Galois , il y a une seule correspondance biunivoque entre les domaines intermédiaires et sous - groupes de son groupe de Galois . ( Les champs intermédiaires sont des champs K satisfaisant F ⊆ K ⊆ E ; ils sont aussi appelés sous - extensions de E / F. )

Description explicite de la correspondance

Pour les extensions finies, la correspondance peut être décrite explicitement comme suit.

• Pour tout sous - groupe H de Gal ( E / F ), le correspondant champ fixe , noté E ^H , est l' ensemble de ces éléments de E qui sont fixés par tous les automorphismes de H .
• Pour tout corps intermédiaire K de E / F , le sous - groupe correspondant est Aut ( E / K ), qui est, l'ensemble de ces automorphismes dans Gal ( E / F ) qui fixent chaque élément de K .

Le théorème fondamental dit que cette correspondance est une correspondance biunivoque si (et seulement si) E / F est une extension de Galois . Par exemple, le champ le plus haut E correspond au sous - groupe trivial de Gal ( E / F ), et le champ de base F correspond au groupe entier Gal ( E / F ).

La notation Gal ( E / F ) n'est utilisée que pour les extensions Galois . Si E / F est Galois, alors Gal ( E / F ) = Aut ( E / F ). Si E / F n'est pas Galois, alors la «correspondance» ne donne qu'une carte injective (mais non surjective ) de à , et une carte surjective (mais non injective) dans le sens inverse. En particulier, si E / F n'est pas Galois, alors F n'est le champ fixe d'aucun sous-groupe d'Aut ( E / F ). ${\ displaystyle \ {{\ text {sous-groupes de Aut}} (E / F) \}}$${\ displaystyle \ {{\ text {sous-champs de}} E / F \}}$

Propriétés de la correspondance

La correspondance a les propriétés utiles suivantes.

• C'est inverser l'inclusion . L'inclusion des sous-groupes H ₁ ⊆ H ₂ est valable si et seulement si l'inclusion des champs E ^{H ₁} ⊇ E ^{H ₂} est vraie .
• Les degrés d'extensions sont liés à des ordres de groupes, d'une manière cohérente avec la propriété d'inversion d'inclusion. Plus précisément, si H est un sous-groupe de Gal ( E / F ), alors | H | = [ E : E ^H ] et | Gal ( E / F ) | / | H | = [ E ^H : F ].
• Le champ E ^H est une extension normale de F (ou, de manière équivalente, une extension de Galois, puisque toute sous-extension d'une extension séparable est séparable) si et seulement si H est un sous-groupe normal de Gal ( E / F ). Dans ce cas, la restriction des éléments de Gal ( E / F ) à E ^H induit un isomorphisme entre Gal ( E ^H / F ) et le groupe de quotient Gal ( E / F ) / H .

Exemple 1

Considérez le terrain

${\ displaystyle K = \ mathbb {Q} \ left ({\ sqrt {2}}, {\ sqrt {3}} \ right) = \ left [\ mathbb {Q} ({\ sqrt {2}}) \ droite] \! ({\ sqrt {3}}).}$

Puisque K est construit à partir du champ de base en joignant √ 2 , alors √ 3 , chaque élément de K peut s'écrire: ${\ displaystyle \ mathbb {Q}}$

${\ displaystyle (a + b {\ sqrt {2}}) + (c + d {\ sqrt {2}}) {\ sqrt {3}}, \ qquad a, b, c, d \ in \ mathbb { Q}.}$

Son groupe Galois comprend les automorphismes de K qui fixent a . De tels automorphismes doivent envoyer √ 2 à √ 2 ou - √ 2 , et envoyer √ 3 à √ 3 ou - √ 3 , puisqu'ils permutent les racines de tout polynôme irréductible. Supposons que f échange √ 2 et - √ 2 , donc ${\ displaystyle G = {\ text {Gal}} (K / \ mathbb {Q})}$

${\ displaystyle f \ left ((a + b {\ sqrt {2}}) + (c + d {\ sqrt {2}}) {\ sqrt {3}} \ right) = (ab {\ sqrt {2 }}) + (cd {\ sqrt {2}}) {\ sqrt {3}} = ab {\ sqrt {2}} + c {\ sqrt {3}} - d {\ sqrt {6}},}$

et g échange √ 3 et - √ 3 , donc

${\ displaystyle g \ left ((a + b {\ sqrt {2}}) + (c + d {\ sqrt {2}}) {\ sqrt {3}} \ right) = (a + b {\ sqrt {2}}) - (c + d {\ sqrt {2}}) {\ sqrt {3}} = a + b {\ sqrt {2}} - c {\ sqrt {3}} - d {\ sqrt {6}}.}$

Ce sont clairement des automorphismes de K , respectant son addition et sa multiplication. Il y a aussi l'automorphisme identitaire e qui fixe chaque élément, et la composition de f et g qui change les signes sur les deux radicaux:

${\ displaystyle (fg) \ left ((a + b {\ sqrt {2}}) + (c + d {\ sqrt {2}}) {\ sqrt {3}} \ right) = (ab {\ sqrt {2}}) - (cd {\ sqrt {2}}) {\ sqrt {3}} = ab {\ sqrt {2}} - c {\ sqrt {3}} + d {\ sqrt {6}} .}$

Puisque l'ordre du groupe de Galois est égal au degré d'extension du champ , il ne peut y avoir d'autres automorphismes: ${\ displaystyle | G | = [K: \ mathbb {Q}] = 4}$

${\ displaystyle G = \ left \ {1, f, g, fg \ right \},}$

qui est isomorphe aux quatre groupes de Klein . Les sous - groupes correspondent aux cinq domaines intermédiaires entre la base et l'extension K . ${\ displaystyle \ mathbb {Q}}$

• Le sous - groupe trivial {1} de correspond à la totalité du champ d'extension K .
• L'ensemble du groupe G correspond au champ de base ${\ displaystyle \ mathbb {Q}.}$
• Le sous-groupe {1, f } correspond au sous-champ puisque f fixe √ 3 . ${\ displaystyle \ mathbb {Q} ({\ sqrt {3}}),}$
• Le sous-groupe {1, g } correspond au sous-champ puisque g fixe √ 2 . ${\ displaystyle \ mathbb {Q} ({\ sqrt {2}}),}$
• Le sous-groupe {1, fg } correspond au sous-champ puisque fg fixe √ 6 . ${\ displaystyle \ mathbb {Q} ({\ sqrt {6}}),}$

Exemple 2

Ce qui suit est le cas le plus simple où le groupe galoisien n'est pas abélien.

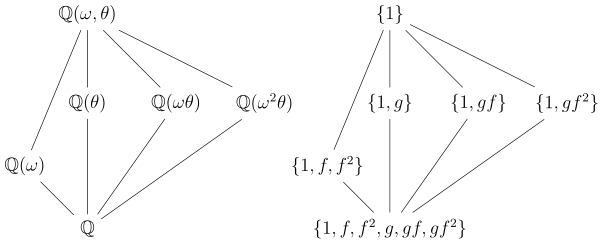
Considérons le champ de division K du polynôme irréductible sur ; c'est-à-dire où θ est une racine cubique de 2, et ω est une racine cubique de 1 (mais pas 1 lui-même). Si nous considérons K à l'intérieur des nombres complexes, nous pouvons prendre , la racine cubique réelle de 2, et Puisque ω a un polynôme minimal , l'extension a le degré: ${\ displaystyle x ^ {3} -2}$${\ displaystyle \ mathbb {Q}}$${\ displaystyle K = \ mathbb {Q} (\ theta, \ omega)}$${\ displaystyle \ theta = {\ sqrt [{3}] {2}}}$${\ displaystyle \ omega = - {\ tfrac {1} {2}} + i {\ tfrac {\ sqrt {3}} {2}}.}$${\ displaystyle x ^ {2} + x + 1}$${\ displaystyle \ mathbb {Q} \ subset K}$

${\ displaystyle [\, K: \ mathbb {Q} \,] = [\, K: \ mathbb {Q} [\, \ theta \,] \,] \ cdot [\, \ mathbb {Q} [\ , \ theta \,]: \ mathbb {Q} \,] = 2 \ cdot 3 = 6}$ ,

avec -basis comme dans l'exemple précédent. Par conséquent, le groupe de Galois comporte six éléments, déterminés par des permutations des trois racines de : ${\ displaystyle \ mathbb {Q}}$${\ displaystyle \ {1, \ theta, \ theta ^ {2}, \ omega, \ omega \ theta, \ omega \ theta ^ {2} \}}$${\ displaystyle G = {\ text {Gal}} (K / \ mathbb {Q})}$${\ displaystyle x ^ {3} -2}$

${\ displaystyle \ alpha _ {1} = \ theta, \ \ alpha _ {2} = \ omega \ theta, \ \ alpha _ {3} = \ omega ^ {2} \ theta.}$

Puisqu'il n'y en a que 3! = 6 de ces permutations, G doit être isomorphe au groupe symétrique de toutes les permutations de trois objets. Le groupe peut être généré par deux automorphismes f et g définis par:

${\ displaystyle f (\ theta) = \ omega \ theta, \ quad f (\ omega) = \ omega,}$

${\ displaystyle g (\ theta) = \ theta, \ quad g (\ omega) = \ omega ^ {2},}$

et obéir aux relations . Leur effet permutations de est - (dans la notation du cycle ): . De plus, g peut être considéré comme la cartographie de conjugaison complexe . ${\ displaystyle G = \ left \ {1, f, f ^ {2}, g, gf, gf ^ {2} \ right \}}$${\ displaystyle f ^ {3} = g ^ {2} = (gf) ^ {2} = 1}$${\ displaystyle \ alpha _ {1}, \ alpha _ {2}, \ alpha _ {3}}$${\ displaystyle f = (123), g = (23)}$

Les sous-groupes de G et les sous-champs correspondants sont les suivants:

• Comme toujours, le groupe trivial {1} ​​correspond au champ entier K , tandis que le groupe entier G au champ de base . ${\ displaystyle \ mathbb {Q}}$
• Le sous-groupe unique d'ordre 3, correspond au sous-domaine du degré deux, puisque le sous-groupe a l' indice deux dans G : ie . En outre, ce sous-groupe est normal, donc le sous-champ est normal au-dessus , étant le champ de division de . Son groupe de Galois sur le corps de base est le groupe quotient , où [ g ] désigne le coset de g modulo H ; c'est-à-dire que son seul automorphisme non trivial est la conjugaison complexe g . ${\ displaystyle H = \ {1, f, f ^ {2} \}}$${\ displaystyle \ mathbb {Q} (\ omega)}$${\ displaystyle [\ mathbb {Q} (\ omega): \ mathbb {Q}] = {\ tfrac {| G |} {| H |}} = 2}$${\ displaystyle \ mathbb {Q}}$${\ displaystyle x ^ {2} + x + 1}$ ${\ displaystyle G / H = \ {[1], [g] \}}$
• Il y a trois sous - groupes d'ordre 2, et correspondant respectivement aux sous - champs Ces sous - zones ont un degré 3 sur étant donné que les sous - groupes ont l' indice 3 en G . Les sous - groupes sont pas normaux dans G , de sorte que les sous - domaines sont pas Galois ou normale sur . En fait, chaque sous-champ ne contient qu'une seule des racines , donc aucune n'a d'automorphismes non triviaux. ${\ displaystyle \ {1, g \}, \ {1, gf \}}$${\ displaystyle \ {1, gf ^ {2} \},}$${\ displaystyle \ mathbb {Q} (\ theta), \ mathbb {Q} (\ omega \ theta), \ mathbb {Q} (\ omega ^ {2} \ theta).}$${\ displaystyle \ mathbb {Q}}$ ${\ displaystyle \ mathbb {Q}}$${\ displaystyle \ alpha _ {1}, \ alpha _ {2}, \ alpha _ {3}}$

Exemple 3

Soit le champ des fonctions rationnelles dans l'indéterminé λ, et considérons le groupe des automorphismes: ${\ displaystyle E = \ mathbb {Q} (\ lambda)}$

${\ displaystyle G = \ left \ {\ lambda, {\ frac {1} {1- \ lambda}}, {\ frac {\ lambda -1} {\ lambda}}, {\ frac {1} {\ lambda }}, {\ frac {\ lambda} {\ lambda -1}}, 1- \ lambda \ right \} \ subset \ mathrm {Aut} (E);}$

ici nous désignons un automorphisme par sa valeur , de sorte que . Ce groupe est isomorphe à (voir: six rapports croisés ). Soit le champ fixe de , de sorte que . ${\ displaystyle \ phi: E \ à E}$${\ displaystyle \ phi (\ lambda)}$${\ displaystyle f (\ lambda) \ mapsto f (\ phi (\ lambda))}$${\ displaystyle S_ {3}}$${\ displaystyle F}$${\ displaystyle G}$${\ displaystyle {\ rm {Gal}} (E / F) = G}$

Si est un sous-groupe de , alors les coefficients du polynôme ${\ displaystyle H}$${\ displaystyle G}$

${\ displaystyle P (T): = \ prod _ {h \ in H} (Th) \ in E [T]}$

générer le champ fixe de . La correspondance de Galois implique que chaque sous-domaine de peut être construit de cette manière. Par exemple, pour , le champ fixe est et si alors le champ fixe est . Le champ fixe de est le champ de base où j est le j -invariant écrit en termes de fonction lambda modulaire : ${\ displaystyle H}$${\ displaystyle E / F}$${\ displaystyle H = \ {\ lambda, 1- \ lambda \}}$${\ displaystyle \ mathbb {Q} (\ lambda (1- \ lambda))}$${\ displaystyle H = \ {\ lambda, {\ tfrac {1} {\ lambda}} \}}$${\ displaystyle \ mathbb {Q} (\ lambda + {\ tfrac {1} {\ lambda}})}$${\ displaystyle G}$${\ displaystyle F = \ mathbb {Q} (j),}$

${\ displaystyle j = {\ frac {256 (1- \ lambda (1- \ lambda)) ^ {3}} {(\ lambda (1- \ lambda)) ^ {2}}} = {\ frac {256 (1- \ lambda + \ lambda ^ {2}) ^ {3}} {\ lambda ^ {2} (1- \ lambda) ^ {2}}} \.}$

Des exemples similaires peuvent être construits pour chacun des groupes de symétrie des solides platoniques car ceux-ci ont également des actions fidèles sur la ligne projective et donc sur . ${\ displaystyle \ mathbb {P} ^ {1} (\ mathbb {C})}$${\ displaystyle \ mathbb {C} (x)}$

Applications

Le théorème classe les champs intermédiaires de E / F en termes de théorie des groupes . Cette traduction entre les champs intermédiaires et les sous-groupes est essentielle pour montrer que l' équation quintique générale n'est pas résoluble par des radicaux (voir théorème d'Abel – Ruffini ). On détermine d'abord les groupes Galois d' extensions radicalaires (extensions de la forme F (α) où α est une n- ième racine d'un élément de F ), puis on utilise le théorème fondamental pour montrer que les extensions solubles correspondent à des groupes solvables .

Les théories telles que la théorie de Kummer et la théorie des champs de classes reposent sur le théorème fondamental.

Cas infini

Étant donné une extension algébrique infinie, nous pouvons toujours la définir comme Galois si elle est normale et séparable. Le problème que l'on rencontre dans le cas infini est que la bijection dans le théorème fondamental ne tient pas car on obtient généralement trop de sous-groupes. Plus précisément, si nous prenons juste chaque sous-groupe, nous pouvons en général trouver deux sous-groupes différents qui fixent le même champ intermédiaire. Nous modifions donc cela en introduisant une topologie sur le groupe de Galois.

Soit une extension galoisienne (possible infinie) et soit le groupe galoisien de l'extension. Laisser ${\ displaystyle E / F}$${\ displaystyle G = {\ text {Gal}} (E / F)}$

soit l'ensemble des groupes galoisiens de toute extension galoisienne intermédiaire finie. Notez que pour tout nous pouvons définir les cartes par . Nous définissons alors la topologie Krull sur d'être le plus faible topologie telle que pour toutes les cartes sont continues, où doter chacun de la topologie discrète. Dit différemment comme une limite inverse des groupes topologiques (où encore chacun est doté de la topologie discrète). Cela fait un groupe profin (en fait, tout groupe profin peut être réalisé comme le groupe galoisien d'une extension galoisienne, voir par exemple). Notez que lorsque est fini, la topologie Krull est la topologie discrète. ${\ displaystyle i \ in I}$${\ displaystyle \ varphi _ {i}: G \ rightarrow G_ {i}}$${\ displaystyle \ sigma \ mapsto \ sigma _ {| L_ {i}}}$${\ displaystyle G}$${\ displaystyle i \ in I}$${\ displaystyle \ varphi _ {i}: G \ rightarrow G_ {i}}$${\ displaystyle G_ {i}}$${\ displaystyle G \ cong \ varprojlim G_ {i}}$${\ displaystyle G_ {i}}$${\ displaystyle G}$${\ displaystyle E / F}$

Maintenant que nous avons défini une topologie sur le groupe de Galois, nous pouvons reformuler le théorème fondamental de l'extension infinie de Galois.

Soit l'ensemble de toutes les extensions de champ intermédiaire fini de et soit l'ensemble de tous les sous-groupes fermés de dotés de la topologie de Krull. Alors il existe une bijection entre et donnée par la carte ${\ displaystyle {\ mathcal {F}}}$${\ displaystyle E / F}$${\ displaystyle {\ mathcal {C}}}$${\ displaystyle G = {\ text {Gal}} (E / F)}$${\ displaystyle {\ mathcal {F}}}$${\ displaystyle {\ mathcal {C}}}$

$${\ displaystyle \ Phi: {\ mathcal {F}} (E / F) \ rightarrow {\ mathcal {C}} (G)}$$

défini par et la carte ${\ displaystyle L \ mapsto {\ text {Gal}} (E / L)}$

$${\ displaystyle \ Gamma: {\ mathcal {C}} (G) \ rightarrow {\ mathcal {F}} (E / F)}$$

défini par . Une chose importante à vérifier est qu'il s'agit d'une carte bien définie, c'est-à-dire qu'il s'agit d'un sous-groupe fermé de pour tous les intermédiaires. Pour une preuve, voir par exemple ${\ displaystyle N \ mapsto {\ text {Fix}} _ {E} (N): = \ {a \ in E ~ | ~ \ sigma (a) = a {\ text {pour tous}} \ sigma \ in N \}}$${\ displaystyle \ Phi}$${\ displaystyle \ Phi (L)}$${\ displaystyle G}$

Les références

Liens externes

• Médias liés au théorème fondamental de la théorie de Galois sur Wikimedia Commons