Bague de groupe - Group ring

En algèbre , un groupe anneau est un module libre et en même temps un anneau , construit de façon naturelle à partir de tout anneau et de tout groupe donnés . En tant que module libre, son anneau de scalaires est l'anneau donné et sa base est l'ensemble des éléments du groupe donné. Comme un anneau, sa loi d'addition est celle du module libre et sa multiplication étend "par linéarité" la loi de groupe donnée sur la base. De façon moins formelle, un anneau de groupe est une généralisation d'un groupe donné, en rajoutant à chaque élément du groupe un « facteur de pondération » d'un anneau donné.

Si l'anneau est commutatif, l'anneau de groupe est également appelé algèbre de groupe , car il s'agit bien d'une algèbre sur l'anneau donné. Une algèbre de groupe sur un corps a une autre structure d' algèbre de Hopf ; dans ce cas, on l'appelle donc algèbre de Hopf de groupe .

L'appareil des anneaux de groupe est particulièrement utile dans la théorie des représentations de groupe .

Définition

Soit G un groupe, écrit multiplicativement, et soit R un anneau. L'anneau de groupe de G sur R , que nous noterons R [ G ] (ou simplement RG ), est l'ensemble des applications f  : G → R de support fini (f(g) est non nul pour un nombre fini d'éléments g seulement) où le produit scalaire du module aF d'un scalaire α dans R et une application f est définie comme la mise en correspondance , et la somme de groupe de modules de deux applications f et g est définie comme la cartographie . Pour transformer le groupe additif R [ G ] en un anneau, nous définissons le produit de f et g comme l'application ${\displaystyle x\mapsto \alpha \cdot f(x)}$${\displaystyle x\mapsto f(x)+g(x)}$

${\displaystyle x\mapsto \sum _{uv=x}f(u)g(v)=\sum _{u\in G}f(u)g(u^{-1}x).}$

La sommation est légitime car f et g sont à support fini, et les axiomes des anneaux sont facilement vérifiés.

Certaines variations dans la notation et la terminologie sont utilisées. En particulier, les applications telles que f  : G → R sont parfois écrites comme ce qu'on appelle des « combinaisons linéaires formelles d'éléments de G , avec des coefficients dans R » :

${\displaystyle \sum _{g\in G}f(g)g,}$

ou simplement

${\displaystyle \sum _{g\in G}f_{g}g,}$

où cela ne crée pas de confusion.

A noter que si l'anneau R est en fait un champ K , alors la structure module de l'anneau de groupe RG est en fait un espace vectoriel sur K .

Exemples

1. Soit G = C ₃ , le groupe cyclique d'ordre 3, de générateur et élément d'identité 1 _G . Un élément r de C [ G ] peut s'écrire sous la forme ${\style d'affichage a}$

${\displaystyle r=z_{0}1_{G}+z_{1}a+z_{2}a^{2}\,}$

où z ₀ , z ₁ et z ₂ sont dans C , les nombres complexes . C'est la même chose qu'un anneau polynomial en variable tel que ie C [ G ] est isomorphe à l'anneau C [ ]/ . ${\style d'affichage a}$${\displaystyle a^{3}=a^{0}=1}$${\style d'affichage a}$${\style d'affichage (a^{3}-1)}$

En écrivant un élément différent s comme , leur somme est ${\displaystyle s=w_{0}1_{G}+w_{1}a+w_{2}a^{2}}$

${\displaystyle r+s=(z_{0}+w_{0})1_{G}+(z_{1}+w_{1})a+(z_{2}+w_{2})a^{2 }\,}$

et leur produit est

${\displaystyle rs=(z_{0}w_{0}+z_{1}w_{2}+z_{2}w_{1})1_{G}+(z_{0}w_{1}+z_{ 1}w_{0}+z_{2}w_{2})a+(z_{0}w_{2}+z_{2}w_{0}+z_{1}w_{1})a^{2} .}$

Remarquons que l'élément d'identité 1 _G de G induit un plongement canonique de l'anneau de coefficients (dans ce cas C ) dans C [ G ] ; cependant à proprement parler l'élément d'identité multiplicatif de C [ G ] est 1⋅1 _G où le premier 1 vient de C et le second de G . L'élément d'identité additif est zéro.

Lorsque G est un groupe non commutatif, il faut veiller à conserver l'ordre des éléments du groupe (et ne pas les commuter accidentellement) lors de la multiplication des termes.

2. Un autre exemple est celui des polynômes de Laurent sur un anneau R : ce ne sont ni plus ni moins que le groupe anneau du groupe cyclique infini Z sur R .

3. Soit Q le groupe de quaternions avec les éléments . Considérons l'anneau de groupe R Q , où R est l'ensemble des nombres réels. Un élément arbitraire de cet anneau de groupe est de la forme ${\displaystyle \{e,{\bar {e}},i,{\bar {i}},j,{\bar {j}},k,{\bar {k}}\}}$

${\displaystyle x_{1}\cdot e+x_{2}\cdot {\bar {e}}+x_{3}\cdot i+x_{4}\cdot {\bar {i}}+x_{5 }\cdot j+x_{6}\cdot {\bar {j}}+x_{7}\cdot k+x_{8}\cdot {\bar {k}}}$

où est un nombre réel. ${\style d'affichage x_{i}}$

La multiplication, comme dans tout autre anneau de groupe, est définie sur la base de l'opération de groupe. Par exemple,

${\displaystyle {\begin{aligned}{\big (}3\cdot e+{\sqrt {2}}\cdot i{\big )}{\big (}{\frac {1}{2}}\cdot {\bar {j}}{\big )}&=(3\cdot e)({\frac {1}{2}}\cdot {\bar {j}})+({\sqrt {2}} \cdot i)({\frac {1}{2}}\cdot {\bar {j}})\\&={\frac {3}{2}}\cdot {\big (}(e)( {\bar {j}}){\big )}+{\frac {\sqrt {2}}{2}}\cdot {\big (}(i)({\bar {j}}){\big )}\\&={\frac {3}{2}}\cdot {\bar {j}}+{\frac {\sqrt {2}}{2}}\cdot k\end{aligned}}. }$

Notez que R Q n'est pas le même que le champ asymétrique des quaternions sur R . En effet, le champ asymétrique des quaternions satisfait des relations supplémentaires dans l'anneau, telles que , alors que dans l'anneau du groupe R Q , n'est pas égal à . Pour être plus précis, l'anneau de groupe R Q a la dimension 8 en tant qu'espace vectoriel réel , tandis que le champ oblique des quaternions a la dimension 4 en tant qu'espace vectoriel réel . ${\displaystyle -1\cdot i=-i}$${\displaystyle -1\cdot i}$${\displaystyle 1\cdot {\bar {i}}}$

4. Un autre exemple d'anneau de groupe non abélien est où se trouve le groupe symétrique sur 3 lettres. Ce n'est pas un domaine intégral puisque nous avons où l'élément est une transposition - une permutation qui échange seulement 1 et 2. Par conséquent, l'anneau de groupe n'a pas besoin d'être un domaine intégral même lorsque l'anneau sous-jacent est un domaine intégral. ${\displaystyle \mathbb {Z} [\mathbb {S} _{3}]}$${\displaystyle \mathbb {S} _{3}}$${\style d'affichage [1-(12)]*[1+(12)]=1-(12)+(12)-(12)(12)=1-1=0}$${\displaystyle (12)\in \mathbb {S} _{3}}$

Quelques propriétés de base

En utilisant 1 pour désigner l'identité multiplicative de l'anneau R , et en désignant l'unité de groupe par 1 _G , l'anneau R [ G ] contient un sous-anneau isomorphe à R , et son groupe d'éléments inversibles contient un sous-groupe isomorphe à G . Pour considérer la fonction indicatrice de {1 _G }, qui est le vecteur f défini par

${\displaystyle f(g)=1\cdot 1_{G}+\sum _{g\not =1_{G}}0\cdot g=\mathbf {1} _{\{1_{G}\}} (g)={\begin{cas}1&g=1_{G}\\0&g\neq 1_{G}\end{cas}},}$

l'ensemble de tous les multiples scalaires de f est un sous-anneau de R [ G ] isomorphe à R . Et si on mappe chaque élément s de G à la fonction indicatrice de { s }, qui est le vecteur f défini par

${\displaystyle f(g)=1\cdot s+\sum _{g\not =s}0\cdot g=\mathbf {1} _{\{s\}}(g)={\begin{cases} 1&g=s\\0&g\neq s\end{cas}}}$

l'application résultante est un homomorphisme de groupe injectif (en ce qui concerne la multiplication, et non l'addition, dans R [ G ]).

Si R et G sont tous les deux commutatifs (c'est-à-dire que R est commutatif et G est un groupe abélien ), R [ G ] est commutatif.

Si H est un sous - groupe de G , alors R [ H ] est un sous - anneau de R [ G ]. De même, si S est un sous-anneau de R , S [ G ] est un sous-anneau de R [ G ].

Si G est un groupe fini d'ordre supérieur à 1, alors R [ G ] a toujours des diviseurs nuls . Par exemple, considérons un élément g de G d'ordre | g | = m > 1. Alors 1 - g est un diviseur nul :

${\displaystyle (1-g)(1+g+\cdots +g^{m-1})=1-g^{m}=1-1=0.}$

Par exemple, considérons le groupe anneau Z [ S ₃ ] et l'élément d'ordre 3 g =(123). Dans ce cas,

${\style d'affichage (1-(123))(1+(123)+(132))=1-(123)^{3}=1-1=0.}$

Un résultat connexe : Si le groupe anneau est premier , alors G n'a pas de sous-groupe normal fini de non-identité (en particulier, G doit être infini). ${\style d'affichage K[G]}$

Preuve : Considérant la contraposée , supposons que est un sous-groupe normal fini de non-identité de . Prenez . Puisque pour tout , on sait , donc . Prenant , nous avons . Par normalité de , commute avec une base de , et donc ${\style d'affichage H}$${\style d'affichage G}$${\displaystyle a=\somme _{h\in H}h}$${\style d'affichage hH=H}$${\style d'affichage h\dans H}$${\style d'affichage ha=a}$${\displaystyle a^{2}=\sum _{h\in H}ha=|H|a}$${\displaystyle b=|H|\,1-a}$${\style d'affichage ab=0}$${\style d'affichage H}$${\style d'affichage a}$${\style d'affichage K[G]}$

${\displaystyle aK[G]b=K[G]ab=0}$.

Et nous voyons qu'ils ne sont pas nuls, ce qui montre qu'ils ne sont pas premiers. Cela montre la déclaration originale. ${\style d'affichage a,b}$${\style d'affichage K[G]}$

Algèbre de groupe sur un groupe fini

Les algèbres de groupe apparaissent naturellement dans la théorie des représentations de groupe des groupes finis . L'algèbre de groupe K [ G ] sur un corps K est essentiellement le groupe anneau, le corps K prenant la place de l'anneau. En tant qu'ensemble et espace vectoriel, c'est l' espace vectoriel libre sur G sur le corps K . C'est-à-dire que pour x dans K [ G ],

${\displaystyle x=\sum _{g\in G}a_{g}g.}$

La structure algébrique sur l'espace vectoriel est définie en utilisant la multiplication dans le groupe :

${\displaystyle g\cdot h=gh,}$

où à gauche, g et h indiquent des éléments de l'algèbre de groupe, tandis que la multiplication à droite est l'opération de groupe (notée par juxtaposition).

Comme la multiplication ci-dessus peut prêter à confusion, on peut également écrire les vecteurs de base de K [ G ] sous la forme e _g (au lieu de g ), auquel cas la multiplication s'écrit :

${\displaystyle e_{g}\cdot e_{h}=e_{gh}.}$

Interprétation en tant que fonctions

En pensant à la espace vectoriel libre comme K à valeurs fonctions sur G , la multiplication de l' algèbre est convolution des fonctions.

Alors que l'algèbre de groupe d'un groupe fini peut être identifiée à l'espace des fonctions sur le groupe, pour un groupe infini celles-ci sont différentes. L'algèbre de groupe, constituée de sommes finies , correspond à des fonctions sur le groupe qui s'annulent pour un nombre cofini de points ; topologiquement (en utilisant la topologie discrète ), celles-ci correspondent à des fonctions à support compact .

Cependant, l'algèbre des groupes K [ G ] et l'espace des fonctions K ^G  := Hom( G , K ) sont duaux : étant donné un élément de l'algèbre des groupes

${\displaystyle x=\sum _{g\in G}a_{g}g}$

et une fonction sur le groupe f  : G → K ces paires pour donner un élément de K via

${\displaystyle (x,f)=\sum _{g\in G}a_{g}f(g),}$

qui est une somme bien définie parce qu'elle est finie.

Représentations d'une algèbre de groupe

En prenant K [ G ] pour une algèbre abstraite, on peut demander des représentations de l'algèbre agissant sur un K -espace vectoriel V de dimension d . Une telle représentation

${\displaystyle {\tilde {\rho }}:K[G]\rightarrow {\mbox{End}}(V)}$

est un homomorphisme algébrique de l'algèbre de groupe à l'algèbre des endomorphismes de V , qui est isomorphe à l'anneau des matrices d × d : . De manière équivalente, il s'agit d'un K [ G ]-module à gauche sur le groupe abélien V . ${\displaystyle \mathrm {Fin} (V)\cong M_{d}(K)}$

En conséquence, une représentation de groupe

${\displaystyle \rho :G\rightarrow {\mbox{Aut}}(V),}$

est un homomorphisme de groupe de G au groupe des automorphismes linéaires de V , qui est isomorphe au groupe linéaire général des matrices inversibles : . Une telle représentation induit une représentation algébrique ${\displaystyle \mathrm {Aut} (V)\cong \mathrm {GL} _{d}(K)}$

${\displaystyle {\tilde {\rho }}:K[G]\rightarrow {\mbox{End}}(V),}$

simplement en laissant et en étendant linéairement. Ainsi, les représentations du groupe correspondent exactement aux représentations de l'algèbre, et les deux théories sont essentiellement équivalentes. ${\displaystyle {\tilde {\rho }}(e_{g})=\rho (g)}$

Représentation régulière

L'algèbre de groupe est une algèbre sur elle-même ; sous la correspondance des représentations sur les modules R et R [ G ], c'est la représentation régulière du groupe.

Écrit comme une représentation, c'est la représentation g ↦ ρ _g avec l'action donnée par , ou ${\displaystyle \rho (g)\cdot e_{h}=e_{gh}}$

${\displaystyle \rho (g)\cdot r=\sum _{h\in G}k_{h}\rho (g)\cdot e_{h}=\sum _{h\in G}k_{h} e_{gh}.}$

Décomposition semi-simple

La dimension de l'espace vectoriel K [ G ] est juste égale au nombre d'éléments du groupe. Le corps K est communément pris pour les nombres complexes C ou les réels R , de sorte que l'on discute les algèbres de groupe C [ G ] ou R [ G ].

L'algèbre de groupe C [ G ] d'un groupe fini sur les nombres complexes est un anneau semi - simple . Ce résultat, le théorème de Maschke , nous permet de comprendre C [ G ] comme un produit fini d' anneaux matriciels avec des entrées dans C . En effet, si nous listons les représentations irréductibles complexes de G comme V _k pour k = 1, . . . , m , ceux - ci correspondent à des homomorphismes de groupe et donc à des homomorphismes algébriques . L'assemblage de ces applications donne un isomorphisme algébrique${\displaystyle \rho _{k}:G\to \mathrm {Aut} (V_{k})}$${\displaystyle {\tilde {\rho }}_{k}:\mathbb {C} [G]\to \mathrm {Fin} (V_{k})}$

${\displaystyle {\tilde {\rho }}:\mathbb {C} [G]\to \bigoplus _{k=1}^{m}\mathrm {End} (V_{k})\cong \bigoplus _ {k=1}^{m}M_{d_{k}}(\mathbb {C} ),}$

où d _k est la dimension de V _k . La sous-algèbre de C [ G ] correspondant à End( V _k ) est l' idéal bilatéral engendré par l' idempotent

${\displaystyle \epsilon _{k}={\frac {d_{k}}{|G|}}\sum _{g\in G}\chi _{k}(g^{-1})\, g,}$

où est le caractère de V _k . Ceux-ci forment un système complet d'idempotents orthogonaux, de sorte que , pour j k , et . L'isomorphisme est étroitement lié à la transformée de Fourier sur les groupes finis . ${\displaystyle \chi _{k}(g)=\mathrm {tr} \,\rho _{k}(g)}$${\displaystyle \epsilon _{k}^{2}=\epsilon _{k}}$${\displaystyle \epsilon _{j}\epsilon _{k}=0}$${\displaystyle 1=\epsilon _{1}+\cdots +\epsilon _{m}}$${\displaystyle {\tilde {\rho }}}$

Pour un domaine plus général K, chaque fois que la caractéristique de K ne divise pas l'ordre du groupe G , alors K [ G ] est semi-simple. Lorsque G est un groupe abélien fini , l'anneau de groupe K [G] est commutatif, et sa structure est facile à exprimer en termes de racines d'unité .

Lorsque K est un corps de caractéristique p qui divise l'ordre de G , l'anneau de groupe n'est pas semi-simple : il a un radical de Jacobson non nul , ce qui donne au sujet correspondant de la théorie des représentations modulaires son propre caractère plus profond.

Centre d'une algèbre de groupe

Le centre de l'algèbre des groupes est l'ensemble des éléments qui commutent avec tous les éléments de l'algèbre des groupes :

${\displaystyle \mathrm {Z} (K[G]):=\left\{z\in K[G]:\forall r\in K[G],zr=rz\right\}.}$

Le centre est égal à l'ensemble des fonctions de classe , c'est-à-dire l'ensemble des éléments constants sur chaque classe de conjugaison

${\displaystyle \mathrm {Z} (K[G])=\left\{\sum _{g\in G}a_{g}g:\forall g,h\in G,a_{g}=a_{ h^{-1}gh}\right\}.}$

Si K = C , l'ensemble des caractères irréductibles de G forme une base orthonormée de Z( K [ G ]) par rapport au produit scalaire

${\displaystyle \left\langle \sum _{g\in G}a_{g}g,\sum _{g\in G}b_{g}g\right\rangle ={\frac {1}{|G |}}\somme _{g\in G}{\bar {a}}_{g}b_{g}.}$

Le groupe sonne sur un groupe infini

On en sait beaucoup moins dans le cas où G est dénombrable infini, ou indénombrable, et c'est un domaine de recherche active. Le cas où R est le corps des nombres complexes est probablement le mieux étudié. Dans ce cas, Irving Kaplansky a prouvé que si a et b sont des éléments de C [ G ] avec ab = 1 , alors ba = 1 . Que cela soit vrai si R est un champ de caractéristique positive reste inconnu.

Une conjecture de longue date de Kaplansky (~1940) dit que si G est un groupe sans torsion , et K est un corps, alors l'anneau de groupe K [ G ] n'a pas de diviseurs nuls non triviaux . Cette conjecture est équivalente à K [ G ] n'ayant pas de nilpotents non triviaux sous les mêmes hypothèses pour K et G .

En fait, la condition que K est un champ peut être assouplie à n'importe quel anneau qui peut être intégré dans un domaine intégral .

La conjecture reste ouverte en toute généralité, mais il a été démontré que certains cas particuliers de groupes sans torsion satisfont la conjecture du diviseur nul. Ceux-ci inclus:

• Groupes de produits uniques (par exemple les groupes commandables , en particulier les groupes gratuits )
• Groupes accommodants élémentaires (par exemple, groupes pratiquement abéliens )
• Groupes diffus - en particulier, les groupes qui agissent librement isométriquement sur les R -arbres, et les groupes fondamentaux des groupes de surface à l'exception des groupes fondamentaux des sommes directes d'une, deux ou trois copies du plan projectif.

Le cas où G est un groupe topologique est discuté plus en détail dans l'article Algèbre de groupe d'un groupe localement compact .

Théorie des catégories

Adjoint

Catégoriquement , la construction de l' anneau du groupe est adjointe à gauche au " groupe d' unités " ; les foncteurs suivants sont une paire adjointe :

${\displaystyle R[-]\colon \mathbf {Grp} \to R\mathbf {{\text{-}}Alg} }$

${\displaystyle (-)^{\times }\colon R\mathbf {{\text{-}}Alg} \to \mathbf {Grp} }$

où prend un groupe à son anneau de groupe sur R , et prend une R -algèbre à son groupe d'unités. ${\style d'affichage R[-]}$${\style d'affichage (-)^{\fois }}$

Lorsque R = Z , cela donne une adjonction entre la catégorie des groupes et la catégorie des anneaux , et l'unité de l'adjonction prend un groupe G à un groupe qui contient des unités triviales : G × {±1} = {± g }. En général, les anneaux de groupe contiennent des unités non triviales. Si G contient des éléments a et b tels que et b ne se normalise pas alors le carré de ${\displaystyle a^{n}=1}$${\displaystyle \langle a\rangle }$

${\displaystyle x=(a-1)b\left(1+a+a^{2}+...+a^{n-1}\right)}$

est nul, d'où . L'élément 1 + x est une unité d'ordre infini. ${\style d'affichage (1+x)(1-x)=1}$

Propriété universelle

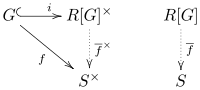
L'adjonction ci-dessus exprime une propriété universelle des anneaux de groupe. Soit R un anneau (commutatif), soit G un groupe et soit S une R -algèbre. Pour tout homomorphisme de groupe , il existe un unique homomorphisme de R -algèbre tel que où i est l'inclusion ${\displaystyle f:G\to S^{\times }}$${\displaystyle {\overline {f}}:R[G]\to S}$${\displaystyle {\overline {f}}\circ i=f}$

${\displaystyle {\begin{aligned}i:G&\longrightarrow R[G]\\g&\longmapsto 1_{R}g\end{aligned}}}$

En d'autres termes, est l'unique homomorphisme faisant commuter le diagramme suivant : ${\displaystyle {\overline {f}}}$

Tout autre anneau satisfaisant cette propriété est canoniquement isomorphe à l'anneau de groupe.

algèbre de Hopf

L'algèbre de groupe K [ G ] a une structure naturelle d' algèbre de Hopf . La comultiplication est définie par , étendu linéairement, et l'antipode est , à nouveau étendu linéairement. ${\displaystyle \Delta (g)=g\fois g}$${\style d'affichage S(g)=g^{-1}}$

Généralisations

L'algèbre des groupes se généralise à l' anneau monoïde et de là à l' algèbre des catégories , dont un autre exemple est l' algèbre d'incidence .

Filtration

Si un groupe a une fonction de longueur – par exemple, s'il y a un choix de générateurs et que l'on prend le mot métrique , comme dans les groupes de Coxeter – alors l'anneau de groupe devient une algèbre filtrée .

Voir également

• Algèbre de groupe d'un groupe localement compact
• Bague monoïde

Théorie des représentations

• Représentation du groupe
• Représentation régulière

Théorie des catégories

• Algèbre catégorielle
• Groupe d'unités
• Algèbre d'incidence
• Carquois algèbre

Remarques

Les références

• AA Bovdi (2001) [1994], "Algèbre de groupe" , Encyclopédie des mathématiques , EMS Press
• Milies, César Polcino; Sehgal, Sudarshan K. Une introduction aux anneaux de groupe . Algèbres et applications, Volume 1. Springer, 2002. ISBN  978-1-4020-0238-0
• Charles W. Curtis , Irving Reiner . Théorie des représentations des groupes finis et algèbres associatives , Interscience (1962)
• DS Passman, La structure algébrique des anneaux de groupe , Wiley (1977)