Groupe quaternion - Quaternion group

Structure algébrique → Théorie des groupes Théorie des groupes
Notions de base Sous-groupe Sous-groupe normal Groupe de quotients Produit (semi-) direct Homomorphismes de groupe noyau image somme directe produit de couronne Facile fini infini continu multiplicatif additif cyclique abélien dièdre nilpotent soluble action Glossaire de la théorie des groupes Liste des sujets de théorie des groupes
Groupes finis Classification des groupes simples finis cyclique en alternance Type de mensonge sporadique Le théorème de Cauchy Le théorème de Lagrange Théorèmes de Sylow théorème de Hall groupe p Groupe abélien élémentaire Groupe Frobenius Multiplicateur de Schur Groupe symétrique S n Klein quatre groupe V Groupe dièdre D n Groupe de quaternions Q Groupe dicyclique Dic n
Groupes discrets Treillis Entiers ( )${\displaystyle \mathbb {Z} }$ Groupe gratuit Groupes modulaires PSL(2, )${\displaystyle \mathbb {Z} }$ SL(2, )${\displaystyle \mathbb {Z} }$ Groupe arithmétique Treillis Groupe hyperbolique
Groupes topologiques et de Lie Solénoïde Cercle GL linéaire général ( n ) Linéaire spécial SL( n ) O orthogonal ( n ) Euclidien E( n ) Spécial orthogonal SO( n ) Unitaire U( n ) Unité spéciale SU( n ) Sp symplectique ( n ) G 2 F 4 E 6 E 7 E 8 Lorentz Poincaré Conforme Difféomorphisme Boucle Groupe de Lie de dimension infinie O(∞) SU(∞) Sp(∞)
Groupes algébriques Groupe algébrique linéaire Groupe réducteur Variété abélienne Courbe elliptique
v t e

Diagramme de cycle de Q ₈ . Chaque couleur spécifie une série de puissances de tout élément connecté à l'élément d'identité e = 1. Par exemple, le cycle en rouge reflète le fait que i ² = e , i ³ = i et i ⁴ = e . Le cycle rouge reflète également que i ² = e , i ³ = i et i ⁴ = e .

Dans la théorie des groupes , le groupe de quaternion Q ₈ (parfois simplement désignée par Q) est un non-commutatif groupe d' ordre huit, isomorphe au sous - ensemble de huit éléments des quaternions pour la multiplication. Il est donné par la présentation de groupe${\style d'affichage \{1,i,j,k,-1,-i,-j,-k\}}$

${\displaystyle \mathrm {Q} _{8}=\langle {\bar {e}},i,j,k\mid {\bar {e}}^{2}=e,\;i^{2 }=j^{2}=k^{2}=ijk={\bar {e}}\rangle ,}$

où e est l'élément d'identité et e commute avec les autres éléments du groupe.

Une autre présentation de Q ₈ est

${\displaystyle \mathrm {Q} _{8}=\langle a,b\mid a^{4}=e,a^{2}=b^{2},ba=a^{-1}b\ rang .}$

Par rapport au groupe dièdre

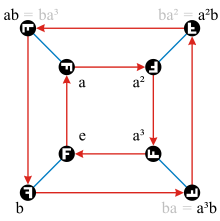
Le groupe de quaternions Q ₈ a le même ordre que le groupe dièdre D ₄ , mais une structure différente, comme le montrent leurs graphiques de Cayley et de cycle :

	Q 8	J 4
Graphique de Cayley	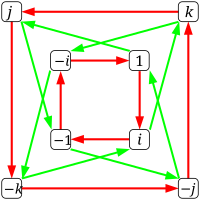Les flèches rouges connectent g → gi , les vertes connectent g → gj .
Graphique du cycle

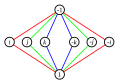
Dans les diagrammes pour D ₄ , les éléments du groupe sont marqués par leur action sur une lettre F dans la représentation de définition R ² . On ne peut pas faire de même pour Q ₈ , car il n'a pas de représentation fidèle dans R ² ou R ³ . D ₄ peut être réalisé comme un sous-ensemble des quaternions divisés de la même manière que Q ₈ peut être considéré comme un sous-ensemble des quaternions.

Table Cayley

La table de Cayley ( table de multiplication) pour Q ₈ est donnée par :

Propriétés

Notez que i , j et k sont tous d' ordre quatre dans Q ₈ et que deux d'entre eux génèrent le groupe entier. Une autre présentation de Q ₈ basée sur seulement deux éléments pour éviter cette redondance est :

${\displaystyle \langle x,y\mid x^{4}=1,x^{2}=y^{2},y^{-1}xy=x^{-1}\rangle .}$

On peut prendre, par exemple, , et . ${\style d'affichage i=x,j=y}$${\style d'affichage k=xy}$

Le groupe quaternion a la propriété inhabituelle d'être hamiltonien : Q ₈ est non abélien, mais chaque sous - groupe est normal . Chaque groupe hamiltonien contient une copie de Q ₈ .

Le groupe quaternion Q ₈ et le groupe dièdre D ₄ sont les deux plus petits exemples d'un groupe non abélien nilpotent .

Le sous - groupe central et collecteur de Q ₈ est le sous-groupe . Le groupe d'automorphisme interne de Q ₈ est donné par le groupe modulo son centre, c'est-à-dire le groupe de facteurs Q ₈ /{e, e }, qui est isomorphe au groupe de Klein V. Le groupe d'automorphisme complet de Q ₈ est isomorphe à S ₄ , le groupe symétrique sur quatre lettres (voir les représentations matricielles ci-dessous), et le groupe d'automorphisme externe de Q ₈ est donc S ₄ /V, qui est isomorphe à S ₃ . ${\displaystyle \{e,{\bar {e}}\}}$

Le groupe de quaternions Q ₈ a cinq classes de conjugaison, { e }, { e }, { i, i }, { j, j }, { k, k }, et donc cinq représentations irréductibles sur les nombres complexes, de dimensions 1, 1,1,1,2 :

Représentation triviale

Représentations de signe avec i,j,k-noyau : Q ₈ a trois sous-groupes normaux maximaux : les sous-groupes cycliques générés par i, j et k respectivement. Pour chaque sous-groupe normal maximal N , nous obtenons une représentation unidimensionnelle factorisée par le groupe quotient à 2 éléments G / N . La représentation envoie des éléments de N à 1, et des éléments extérieurs à N à -1.

Représentation bidimensionnelle : Décrit ci-dessous dans Représentations matricielles .

La table de caractères de Q ₈ s'avère être la même que celle de D ₄ :

Puisque les caractères irréductibles des lignes ci-dessus ont des valeurs réelles, cela donne la décomposition de l' algèbre de groupe réelle de en idéaux bilatéraux minimaux : , où les idempotents correspondent aux irréductibles : , de sorte que${\displaystyle \chi _{\rho }}$${\style d'affichage G=Q_{8}}$${\displaystyle \textstyle \mathbb {R} [Q_{8}]\ =\ \bigoplus _{\rho }(e_{\rho })}$ ${\displaystyle e_{\rho }\in \mathbb {R} [Q_{8}]}$${\displaystyle \textstyle e_{\rho }={\frac {\dim(\rho )}{|G|}}\sum _{g\in G}\chi _{\rho }(g^{-1 })g}$

${\displaystyle e_{\text{triv}}={\tfrac {1}{8}}(e+{\bar {e}}+i+{\bar {i}}+j+{\bar {j}}+ k+{\bar {k}})}$

${\displaystyle e_{i{\text{-ker}}}={\tfrac {1}{8}}(e+{\bar {e}}+i+{\bar {i}}-j-{\bar {j}}-k-{\bar {k}})}$

${\displaystyle e_{j{\text{-ker}}}={\tfrac {1}{8}}(e+{\bar {e}}-i-{\bar {i}}+j+{\bar {j}}-k-{\bar {k}})}$

${\displaystyle e_{k{\text{-ker}}}={\tfrac {1}{8}}(e+{\bar {e}}-i-{\bar {i}}-j-{\ barre {j}}+k+{\bar {k}})}$

${\displaystyle e_{2}={\tfrac {2}{8}}(2e-2{\bar {e}})={\tfrac {1}{2}}(e-{\bar {e} })}$.

Chacun de ces idéaux irréductibles est isomorphe à une algèbre simple centrale réelle , les quatre premiers au corps réel . Le dernier idéal est isomorphe au champ oblique des quaternions par la correspondance :${\displaystyle \mathbb {R} }$${\style d'affichage (e_{2})}$ ${\displaystyle \mathbb {H} }$

${\displaystyle \textstyle {\frac {1}{2}}(e-{\bar {e}})\longleftrightarrow 1,\ \ {\frac {1}{2}}(i-{\bar {i }})\longleftrightarrow i,\ \ {\frac {1}{2}}(j-{\bar {j}})\longleftrightarrow j,\ \ {\frac {1}{2}}(k-{ \bar {k}})\longleftrightarrow k.}$

De plus, l'homomorphisme de projection donné par a un noyau idéal généré par l'idempotent :${\displaystyle \mathbb {R} [Q_{8}]\to (e_{2})\cong \mathbb {H} }$${\displaystyle r\mapsto re_{2}}$

${\displaystyle e_{2}^{\perp }\ =\ \textstyle e_{1}+e_{i{\text{-ker}}}+e_{j{\text{-ker}}}+e_{ k{\text{-ker}}}\ =\ {\frac {1}{2}}(e+{\bar {e}}),}$

de sorte que les quaternions peuvent également être obtenus sous forme d' anneau quotient . ${\displaystyle \mathbb {R} [Q_{8}]/(e+{\bar {e}})\cong \mathbb {H} }$

L'algèbre des groupes complexes est donc , où est l'algèbre des biquaternions . ${\displaystyle \mathbb {C} [Q_{8}]\cong \mathbb {C} ^{\oplus 4}\oplus M_{2}(\mathbb {C} )}$${\displaystyle M_{2}(\mathbb {C} )\cong \mathbb {H} \otimes _{\mathbb {R} }\!\mathbb {C} \cong \mathbb {H} \oplus \mathbb { H} }$

Représentations matricielles

Table de multiplication du groupe quaternion en tant que sous-groupe de SL (2, C ). Les entrées sont représentées par des secteurs correspondant à leurs arguments : 1 (vert), i (bleu), -1 (rouge), - i (jaune).

Le complexe irréductible en deux dimensions une représentation décrite ci - dessus donne le groupe de quaternion Q ₈ en tant que sous - groupe du groupe linéaire . Le groupe des quaternions est un sous-groupe multiplicatif de l'algèbre des quaternions , qui a une représentation régulière par multiplication à gauche sur lui-même considéré comme un espace vectoriel complexe à base , ce qui correspond à l' application C- linéaire . La représentation résultante est donnée par : ${\displaystyle \operatorname {GL} (2,\mathbb {C} )}$${\displaystyle \mathbb {H} =\mathbb {R} 1+\mathbb {R} i+\mathbb {R} j+\mathbb {R} k=\mathbb {C} 1+\mathbb {C} j}$ ${\displaystyle \rho :\mathbb {H} \to \mathrm {M} _{2}(\mathbb {C} )}$${\style d'affichage \{1,j\}}$${\displaystyle z\in \mathbb {H} }$${\displaystyle \rho _{z}:a{+}jb\mapsto z\cdot (a{+}jb)}$${\displaystyle \rho :\mathrm {Q} _{8}\to \mathrm {GL} (2,\mathbb {C} ),\ g\mapsto \rho _{g},}$

${\displaystyle {\begin{matrix}e\mapsto {\begin{pmatrix}1&0\\0&1\end{pmatrix}}&i\mapsto {\begin{pmatrix}i&0\\0&\!\!\!\!- i\end{pmatrix}}&j\mapsto {\begin{pmatrix}0&\!\!\!\!-1\\1&0\end{pmatrix}}&k\mapsto {\begin{pmatrix}0&\!\! \!\!-i\\\!\!\!-i&0\end{pmatrix}}\\{\overline {e}}\mapsto {\begin{pmatrix}\!\!\!-1&0\\0& \!\!\!\!-1\end{pmatrix}}&{\overline {i}}\mapsto {\begin{pmatrix}\!\!\!-i&0\\0&i\end{pmatrix}}& {\overline {j}}\mapsto {\begin{pmatrix}0&1\\\!\!\!-1&0\end{pmatrix}}&{\overline {k}}\mapsto {\begin{pmatrix}0&i\ \i&0\end{pmatrix}}.\end{matrix}}}$

Étant donné que toutes les matrices ci-dessus ont un déterminant d'unité, il s'agit d'une représentation de Q ₈ dans le groupe linéaire spécial SL(2, C ).

Une variante donne une représentation par matrices unitaires (tableau à droite). Soit correspondant à l'application linéaire , donc qui est donnée par : ${\displaystyle g\in Q_{8}}$${\displaystyle \rho _{g}:a{+}bj\mapsto (a{+}bj)\cdot jg^{-1}j^{-1}}$${\displaystyle \rho :\mathrm {Q} _{8}\to \mathrm {SU} (2)}$

${\displaystyle {\begin{matrix}e\mapsto {\begin{pmatrix}1&0\\0&1\end{pmatrix}}&i\mapsto {\begin{pmatrix}i&0\\0&\!\!\!\!- i\end{pmatrix}}&j\mapsto {\begin{pmatrix}0&1\\\!\!\!-1&0\end{pmatrix}}&k\mapsto {\begin{pmatrix}0&i\\i&0\end{pmatrix }}\\{\overline {e}}\mapsto {\begin{pmatrix}\!\!\!-1&0\\0&\!\!\!\!-1\end{pmatrix}}&{\overline {i}}\mapsto {\begin{pmatrix}\!\!\!-i&0\\0&i\end{pmatrix}}&{\overline {j}}\mapsto {\begin{pmatrix}0&\!\! \!\!-1\\1&0\end{pmatrix}}&{\overline {k}}\mapsto {\begin{pmatrix}0&\!\!\!\!-i\\\!\!\! -i&0\end{pmatrix}}.\end{matrice}}}$

Il est à noter que les physiciens utilisent exclusivement une convention différente pour la représentation matricielle pour prendre contact avec les matrices de Pauli habituelles : ${\displaystyle \mathrm {SU} (2)}$

${\displaystyle {\begin{matrix}&e\mapsto {\begin{pmatrix}1&0\\0&1\end{pmatrix}}=\quad \,1_{2\times 2}&i\mapsto {\begin{pmatrix}0& \!\!\!-i\!\\\!\!-i\!\!&0\end{pmatrix}}=-i\sigma _{x}&j\mapsto {\begin{pmatrix}0&\! \!\!-1\!\\1&0\end{pmatrix}}=-i\sigma _{y}&k\mapsto {\begin{pmatrix}\!\!-i\!\!&0\\0&i\ end{pmatrix}}=-i\sigma _{z}\\&{\overline {e}}\mapsto {\begin{pmatrix}\!\!-1\!&0\\0&\!\!\! -1\!\end{pmatrix}}=-1_{2\times 2}&{\overline {i}}\mapsto {\begin{pmatrix}0&i\\i&0\end{pmatrix}}=\,\, \,\,i\sigma _{x}&{\overline {j}}\mapsto {\begin{pmatrix}0&1\\\!\!-1\!\!&0\end{pmatrix}}=\, \,\,\,i\sigma _{y}&{\overline {k}}\mapsto {\begin{pmatrix}i&0\\0&\!\!\!-i\!\end{pmatrix}}= \,\,\,\,i\sigma _{z}.\end{matrice}}}$

Ce choix particulier est pratique et élégant lorsque l'on décrit les états de spin-1/2 dans la base et considère les opérateurs d'échelle de moment angulaire . ${\style d'affichage ({\vec {J}}^{2},J_{z})}$ ${\displaystyle J_{\pm }=J_{x}\pm iJ_{y}}$

Table de multiplication du groupe quaternion en tant que sous-groupe de SL(2,3) . Les éléments du champ sont notés 0,+,−.

Il y a aussi une action importante de Q ₈ sur l'espace vectoriel à 2 dimensions sur le corps fini F ₃ = {0,1,−1} (tableau à droite). Une représentation modulaire est donnée par ${\displaystyle \rho :\mathrm {Q} _{8}\to \mathrm {SL} (2,3)}$

${\displaystyle {\begin{matrix}e\mapsto {\begin{pmatrix}1&0\\0&1\end{pmatrix}}&i\mapsto {\begin{pmatrix}1&1\\1&\!\!\!\!- 1\end{pmatrix}}&j\mapsto {\begin{pmatrix}\!\!\!-1&1\\1&1\end{pmatrix}}&k\mapsto {\begin{pmatrix}0&\!\!\!\ !-1\\1&0\end{pmatrix}}\\{\overline {e}}\mapsto {\begin{pmatrix}\!\!\!-1&0\\0&\!\!\!\!-1 \end{pmatrix}}&{\overline {i}}\mapsto {\begin{pmatrix}\!\!\!-1&\!\!\!\!-1\\\!\!\!-1&1 \end{pmatrix}}&{\overline {j}}\mapsto {\begin{pmatrix}1&\!\!\!\!-1\\\!\!\!-1&\!\!\!\ !-1\end{pmatrix}}&{\overline {k}}\mapsto {\begin{pmatrix}0&1\\\!\!\!-1&0\end{pmatrix}}.\end{matrix}}}$

Cette représentation peut être obtenue à partir du champ d'extension F ₉ = F ₃ [ k ] = F ₃ 1 + F ₃ k , où k ² = −1 et le groupe multiplicatif ( F ₉ ) ^× a des générateurs ±( k +1), ± ( k - 1) d'ordre 8. les deux dimensions F ₃ espace -vector F ₉ admet les applications linéaires pour z dans F ₉ , ainsi que les automorphismes de Frobenius satisfaisant et . Alors les matrices de représentation ci-dessus sont , , , et . ${\displaystyle \mu _{z}(a+bk)=z\cdot (a+bk)}$ ${\displaystyle \phi (a+bk)=(a+bk)^{3}}$${\displaystyle \phi ^{2}=\mu _{1}}$${\displaystyle \phi \mu _{z}=\mu _{\phi (z)}\phi }$${\displaystyle \rho ({\bar {e}})=\mu _{-1}}$${\displaystyle \rho (i)=\mu _{k+1}\phi }$${\displaystyle \rho (j)=\mu _{k-1}\phi }$${\displaystyle \rho (k)=\mu _{k}}$

La représentation ci-dessus réalise Q ₈ comme un sous-groupe normal de GL(2, 3) . Ainsi, pour chaque matrice , nous avons un automorphisme de groupe défini par , avec . En fait, ceux-ci donnent le groupe d'automorphisme complet comme: ${\displaystyle m\in \mathrm {GL} (2,3)}$${\displaystyle \psi _{m}:Q_{8}\to Q_{8}}$${\displaystyle \psi _{m}(g)=mgm^{-1}}$${\displaystyle \psi _{I}=\psi _{-I}=\mathrm {id} _{Q_{8}}}$

${\displaystyle \mathrm {Aut} (Q_{8})\cong \mathrm {PGL} (2,3)=\mathrm {GL} (2,3)/\{\pm I\}\cong S_{4 }}$,

Ceci est isomorphe au groupe symétrique S ₄ puisque les applications linéaires permutent les quatre sous-espaces à une dimension de , c'est-à-dire les quatre points de l' espace projectif . ${\displaystyle m:\mathbb {F} _{3}^{2}\to \mathbb {F} _{3}^{2}}$${\displaystyle \mathbb {F} _{3}^{2}}$ ${\displaystyle \mathbb {P} _{\mathbb {F} _{3}}^{1}=\mathrm {PG} (1,3)}$

Aussi, cette représentation permute les huit vecteurs non nuls de ( F ₃ ) ² , donnant un plongement de Q ₈ dans le groupe symétrique S _8, en plus des plongements donnés par les représentations régulières.

Groupe Galois

Comme Richard Dean l'a montré en 1981, le groupe des quaternions peut être présenté comme le groupe de Galois Gal(T/ Q ) où Q est le corps des nombres rationnels et T est le corps de division sur Q du polynôme

${\displaystyle x^{8}-72x^{6}+180x^{4}-144x^{2}+36}$.

Le développement utilise le théorème fondamental de la théorie de Galois pour spécifier quatre champs intermédiaires entre Q et T et leurs groupes de Galois, ainsi que deux théorèmes sur l'extension cyclique de degré quatre sur un champ.

Groupe quaternion généralisé

Un groupe de quaternions généralisé Q _{4 n} d'ordre 4 n est défini par la présentation

${\displaystyle \langle x,y\mid x^{2n}=y^{4}=1,x^{n}=y^{2},y^{-1}xy=x^{-1} \rangle }$

pour un entier n 2 , avec le groupe quaternion usuel donné par n = 2. Coxeter appelle Q _{4 n} le groupe dicyclique , un cas particulier du groupe polyédrique binaire et lié au groupe polyédrique et au groupe dièdre . Le groupe quaternion généralisé peut être réalisé comme le sous-groupe de généré par ${\displaystyle \langle 2,2,n\rangle }$ ${\displaystyle \langle \ell ,m,n\rangle }$ ${\style d'affichage (p,q,r)}$ ${\style d'affichage (2,2,n)}$${\displaystyle \operatorname {GL} _{2}(\mathbb {C} )}$

${\displaystyle \left({\begin{array}{cc}\omega _{n}&0\\0&{\overline {\omega }}_{n}\end{array}}\right){\mbox{ et }}\gauche({\begin{array}{cc}0&-1\\1&0\end{array}}\right)}$

où . Il peut également être réalisé comme le sous-groupe de quaternions unitaires générés par et . ${\displaystyle \omega _{n}=e^{i\pi /n}}$${\displaystyle x=e^{i\pi /n}}$${\style d'affichage y=j}$

Les groupes de quaternions généralisés ont la propriété que chaque sous-groupe abélien est cyclique. On peut montrer qu'un p -groupe fini avec cette propriété (chaque sous-groupe abélien est cyclique) est soit cyclique, soit un groupe quaternion généralisé tel que défini ci-dessus. Une autre caractérisation est qu'un p -groupe fini dans lequel il existe un sous-groupe unique d'ordre p est soit cyclique, soit un groupe à 2 groupes isomorphe à quaternion généralisé. En particulier, pour un corps fini F de caractéristique impaire, le sous-groupe 2-Sylow de SL ₂ ( F ) est non abélien et n'a qu'un seul sous-groupe d'ordre 2, donc ce sous-groupe 2-Sylow doit être un groupe de quaternions généralisé, ( Gorenstein 1980 , p.42). Soit p ^r la taille de F , où p est premier, la taille du sous-groupe 2-Sylow de SL ₂ ( F ) est 2 ⁿ , où n = ord ₂ ( p ² − 1) + ord ₂ ( r ) .

Le théorème de Brauer-Suzuki montre que les groupes dont les 2-sous-groupes de Sylow sont des quaternions généralisés ne peuvent pas être simples.

Une autre terminologie réserve le nom de "groupe quaternion généralisé" à un groupe dicyclique d'ordre une puissance 2, ce qui admet la présentation

${\displaystyle \langle x,y\mid x^{2^{m}}=y^{4}=1,x^{2^{m-1}}=y^{2},y^{- 1}xy=x^{-1}\rangle .}$

Voir également

• 16 cellules
• Groupe tétraédrique binaire
• algèbre de Clifford
• Groupe dicyclique
• quaternion intégral de Hurwitz
• Liste des petits groupes

Remarques

Les références

• Artin, Michael (1991), Algèbre , Prentice Hall, ISBN 978-0-13-004763-2
• Brown, Kenneth S. (1982), Cohomologie des groupes (3e éd.), Springer-Verlag, ISBN 978-0-387-90688-1
• Cartan, Henri ; Eilenberg, Samuel (1999), Algèbre Homologique , Princeton University Press, ISBN 978-0-691-04991-5
• Coxeter, HSM & Moser, WOJ (1980). Générateurs et relations pour les groupes discrets . New York : Springer-Verlag. ISBN 0-387-09212-9.
• Dean, Richard A. (1981) "Un polynôme rationnel dont le groupe est les quaternions", American Mathematical Monthly 88:42-5.
• Gorenstein, D. (1980), Groupes finis , New York : Chelsea, ISBN 978-0-8284-0301-6, MR  0569209
• Johnson, David L. (1980), Topics in the theory of group presentations , Cambridge University Press , ISBN 978-0-521-23108-4, MR  0695161
• Rotman, Joseph J. (1995), Une introduction à la théorie des groupes (4e éd.), Springer-Verlag, ISBN 978-0-387-94285-8
• PR Girard (1984) "Le groupe quaternion et la physique moderne", European Journal of Physics 5:25-32.
• Hall, Marshall (1999), La théorie des groupes (2e éd.), AMS Bookstore, ISBN 0-8218-1967-4
• Kurosh, Alexander G. (1979), Théorie des groupes , Librairie AMS, ISBN 0-8284-0107-1

Liens externes

• Weisstein, Eric W. "Groupe Quaternion" . MathWorld .
• Groupes quaternions sur GroupNames
• Groupe Quaternion sur GroupProps
• Conrad, Keith. "Quaternions généralisés"