Groupe libre - Free group

Structure algébrique → Théorie des groupes Théorie des groupes
Notions de base Sous-groupe Sous-groupe normal Groupe quotient Produit (semi-) direct Homomorphismes de groupe noyau image somme directe produit de couronne Facile fini infini continu multiplicatif additif cyclique abélien dièdre nilpotent soluble Glossaire de la théorie des groupes Liste des sujets de théorie des groupes
Groupes finis Classification des groupes simples finis cyclique en alternance Type de mensonge sporadique Le théorème de Cauchy Le théorème de Lagrange Théorèmes de Sylow théorème de Hall groupe p Groupe abélien élémentaire Groupe Frobenius Multiplicateur de Schur Groupe symétrique S n Klein quatre groupe V Groupe dièdre D n Groupe de quaternions Q Groupe dicyclique Dic n
Groupes discrets Treillis Entiers ( Z ) Groupe gratuit Groupes modulaires PSL(2, Z ) SL(2, Z ) Groupe arithmétique Treillis Groupe hyperbolique
Groupes topologiques et de Lie Solénoïde Cercle GL linéaire général ( n ) Linéaire spécial SL( n ) O orthogonal ( n ) Euclidien E( n ) Spécial orthogonal SO( n ) Unitaire U( n ) Unité spéciale SU( n ) Sp symplectique ( n ) G 2 F 4 E 6 E 7 E 8 Lorentz Poincaré Conforme Difféomorphisme Boucle Groupe de Lie de dimension infinie O(∞) SU(∞) Sp(∞)
Groupes algébriques Groupe algébrique linéaire Groupe réducteur Variété abélienne Courbe elliptique
v t e

Diagramme montrant à quoi ressemblerait le graphique de Cayley pour le groupe libre sur deux générateurs. Chaque sommet représente un élément du groupe libre, et chaque arête représente la multiplication par a ou b .

En mathématiques , le groupe libre F _S sur un ensemble donné S se compose de tous les mots qui peuvent être construits à partir des membres de S , considérant que deux mots sont différents à moins que leur égalité ne découle des axiomes du groupe (par exemple st = suu ⁻¹ t , mais s ≠ t ^-1 pour s , t , u ∈ s ). Les membres de S sont appelés générateurs de F _S , et le nombre de générateurs est le rang du groupe libre. Un groupe arbitraire G est dit libre s'il est isomorphe à F _S pour un sous-ensemble S de G , c'est-à-dire s'il existe un sous-ensemble S de G tel que chaque élément de G peut s'écrire exactement d'une manière comme un produit de de nombreux éléments de S et leurs inverses (sans tenir compte des variations triviales telles que st = suu ⁻¹ t ).

Une notion voisine mais différente est celle d'un groupe abélien libre ; les deux notions sont des instances particulières d'un objet libre de l'algèbre universelle . En tant que tels, les groupes libres sont définis par leur propriété universelle .

Histoire

Les groupes libres sont apparus d'abord dans l'étude de la géométrie hyperbolique , comme exemples de groupes fuchsiens (groupes discrets agissant par isométries sur le plan hyperbolique ). Dans un article de 1882, Walther von Dyck a souligné que ces groupes ont les présentations les plus simples possibles . L'étude algébrique des groupes libres a été initiée par Jakob Nielsen en 1924, qui leur a donné leur nom et établi nombre de leurs propriétés fondamentales. Max Dehn a réalisé le lien avec la topologie et a obtenu la première preuve du théorème de Nielsen-Schreier complet . Otto Schreier a publié une preuve algébrique de ce résultat en 1927, et Kurt Reidemeister a inclus un traitement complet des groupes libres dans son livre de 1932 sur la topologie combinatoire . Plus tard dans les années 1930, Wilhelm Magnus a découvert le lien entre la série centrale inférieure des groupes libres et les algèbres de Lie libres .

Exemples

Le groupe ( Z ,+) d' entiers est libre de rang 1 ; un groupe électrogène est S = {1}. Les entiers sont également un groupe abélien libre , bien que tous les groupes libres de rang soient non abéliens. Un groupe libre sur un ensemble de deux éléments S apparaît dans la preuve du paradoxe de Banach-Tarski et y est décrit. ${\style d'affichage \geq 2}$

D'autre part, tout groupe fini non trivial ne peut pas être libre, puisque les éléments d'un ensemble générateur libre d'un groupe libre ont un ordre infini.

En topologie algébrique , le groupe fondamental d'un bouquet de k cercles (un ensemble de k boucles n'ayant qu'un seul point en commun) est le groupe libre sur un ensemble de k éléments.

Construction

Le groupe libre F _S avec groupe électrogène libre S peut être construit comme suit. S est un ensemble de symboles, et nous supposons que pour chaque s dans S il y a un symbole "inverse" correspondant, s ^-1 , dans un ensemble S ^-1 . Soit T  =  S  ∪  S ^-1 , et de définir un mot en S pour être tout produit écrit des éléments de T . C'est-à-dire qu'un mot dans S est un élément du monoïde généré par T . Le mot vide est le mot sans aucun symbole. Par exemple, si S  = { a ,  b ,  c }, alors T  = { a ,  a ^-1 ,  b ,  b ^-1 ,  c ,  c ^-1 }, et

${\displaystyle ab^{3}c^{-1}ca^{-1}c\,}$

est un mot dans S .

Si un élément de S se trouve immédiatement à côté de son inverse, le mot peut être simplifié en omettant la paire c, c ^-1 :

${\displaystyle ab^{3}c^{-1}ca^{-1}c\;\;\longrightarrow \;\;ab^{3}\,a^{-1}c.}$

Un mot qui ne peut pas être simplifié davantage est appelé réduit .

Le groupe libre F _S est défini comme étant le groupe de tous les mots réduits dans S , avec concaténation de mots (suivie d'une réduction si nécessaire) comme opération de groupe. L'identité est le mot vide.

Un mot est dit cycliquement réduit si sa première et sa dernière lettre ne sont pas inverses l'une de l'autre. Chaque mot est conjugué à un mot cycliquement réduit, et un conjugué cycliquement réduit d'un mot cycliquement réduit est une permutation cyclique des lettres du mot. Par exemple b ^-1 abcb n'est pas cycliquement réduit, mais est conjugué à abc , qui est cycliquement réduit. Les seuls conjugués cycliquement réduits de abc sont abc , bca et cab .

Propriété universelle

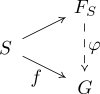
Le groupe libre F _S est le groupe universel engendré par l'ensemble S . Ceci peut être formalisé par la propriété universelle suivante : étant donné toute fonction f de S dans un groupe G , il existe un unique homomorphisme φ :  F _S  →  G faisant commuter le diagramme suivant (où l'application sans nom dénote l' inclusion de S dans F _S ):

C'est-à-dire que les homomorphismes F _S  →  G sont en correspondance biunivoque avec les fonctions S  →  G . Pour un groupe non libre, la présence de relations restreindrait les images possibles des générateurs sous un homomorphisme.

Pour voir comment cela se rapporte à la définition constructive, pensez au mappage de S à F _S comme l'envoi de chaque symbole à un mot composé de ce symbole. Pour construire φ pour le f donné , notez d'abord que φ envoie le mot vide à l'identité de G et qu'il doit être en accord avec f sur les éléments de S . Pour les mots restants (constitués de plus d'un symbole), φ peut être étendu de manière unique, puisqu'il s'agit d'un homomorphisme, c'est-à-dire φ ( ab ) = φ ( a ) φ ( b ).

La propriété ci-dessus caractérise les groupes libres jusqu'à l' isomorphisme , et est parfois utilisée comme définition alternative. Elle est connue sous le nom de propriété universelle des groupes libres, et l'ensemble générateur S est appelé base de F _S . La base d'un groupe libre n'est pas déterminée de manière unique.

Être caractérisé par une propriété universelle est la caractéristique standard des objets libres en algèbre universelle . Dans le langage de la théorie des catégories , la construction du groupe libre (similaire à la plupart des constructions d'objets libres) est un foncteur de la catégorie des ensembles à la catégorie des groupes . Ce foncteur est adjoint au foncteur d' oubli des groupes aux ensembles.

Faits et théorèmes

Certaines propriétés des groupes libres découlent facilement de la définition :

1. Tout groupe G est l'image homomorphe d'un groupe libre F( S ). Soit S un ensemble de générateurs de G . L'application naturelle f : F( S ) → G est un épimorphisme , ce qui prouve l'affirmation. De manière équivalente, G est isomorphe à un groupe quotient d'un groupe libre F( S ). Le noyau de φ est un ensemble de relations dans la présentation de G . Si S peut être choisi pour être fini ici, alors G est appelé de génération finie .
2. Si S a plus d'un élément, alors F( S ) n'est pas abélien , et en fait le centre de F( S ) est trivial (c'est-à-dire qu'il n'est constitué que de l'élément identité).
3. Deux groupes libres F( S ) et F( T ) sont isomorphes si et seulement si S et T ont la même cardinalité . Cette cardinalité est appelée rang du groupe libre F . Ainsi pour tout nombre cardinal k , il existe, à isomorphisme près, exactement un groupe libre de rang k .
4. Un groupe libre de rang fini n > 1 a un taux de croissance exponentiel d'ordre 2 n − 1.

Voici quelques autres résultats connexes :

1. Le théorème de Nielsen-Schreier : Tout sous - groupe d'un groupe libre est libre.
2. Un groupe libre de rang k a clairement des sous-groupes de chaque rang inférieur à k . De façon moins évidente, un groupe libre ( non abélien ! ) de rang au moins 2 a des sous-groupes de tous les rangs dénombrables .
3. Le sous - groupe de commutateurs d'un groupe libre de rang k > 1 est de rang infini ; par exemple pour F( a , b ), il est librement généré par les commutateurs [ a ^m , b ⁿ ] pour m et n non nuls .
4. Le groupe libre en deux éléments est SQ universel ; ce qui précède suit car tout groupe universel SQ a des sous-groupes de tous les rangs dénombrables.
5. Tout groupe qui agit sur un arbre, librement et en conservant l' orientation , est un groupe libre de rang dénombrable (donné par 1 plus la caractéristique d'Euler du graphe quotient ).
6. Le graphe de Cayley d'un groupe libre de rang fini, par rapport à un générateur libre, est un arbre sur lequel le groupe agit librement en préservant l'orientation.
7. L' approche groupoïde de ces résultats, donnée dans l'ouvrage de PJ Higgins ci-dessous, est en quelque sorte extraite d'une approche utilisant des espaces couvrants . Il permet des résultats plus puissants, par exemple sur le théorème de Grushko , et une forme normale pour le groupoïde fondamental d'un graphe de groupes. Dans cette approche, il y a une utilisation considérable de groupoïdes libres sur un graphe orienté.
8. Le théorème de Grushko a pour conséquence que si un sous-ensemble B d'un groupe libre F sur n éléments génère F et possède n éléments, alors B génère F librement.

Groupe abélien gratuit

Le groupe abélien libre sur un ensemble S est définie par sa propriété universelle de la manière analogue, avec les modifications évidentes: Soit un couple ( F , φ ), où F est un groupe abélien et φ : S → F est une fonction. F est dit le groupe abélien libre sur S par rapport à φ si pour tout groupe abélien G et toute fonction ψ : S → G , il existe un unique homomorphisme f : F → G tel que

f ( φ ( s )) = ψ ( s ), pour tout s dans S .

Le groupe abélien libre sur S peut être explicitement identifié comme le groupe libre F( S ) modulo le sous-groupe engendré par ses commutateurs, [F( S ), F( S )], c'est-à-dire son abélianisation . En d'autres termes, le groupe abélien libre sur S est l'ensemble des mots qui ne se distinguent qu'à l'ordre des lettres près. Le rang d'un groupe libre peut donc aussi être défini comme le rang de son abélianisation en tant que groupe abélien libre.

Les problèmes de Tarski

Vers 1945, Alfred Tarski a demandé si les groupes libres sur deux ou plusieurs générateurs ont la même théorie du premier ordre , et si cette théorie est décidable . Sela (2006) a répondu à la première question en montrant que deux groupes libres non abéliens ont la même théorie du premier ordre, et Kharlampovich & Myasnikov (2006) ont répondu aux deux questions, montrant que cette théorie est décidable.

Une question similaire non résolue (à partir de 2011) dans la théorie des probabilités libres demande si les algèbres de groupe de von Neumann de deux groupes libres non abéliens de type fini sont isomorphes.

Voir également

• Groupe électrogène d'un groupe
• Présentation d'un groupe
• Transformation de Nielsen , une factorisation des éléments du groupe d' automorphisme d' un groupe libre
• Forme normale pour les groupes libres et produit libre des groupes
• Produit gratuit

Remarques

Les références

• Kharlampovitch, Olga ; Myasnikov, Alexeï (2006). « Théorie élémentaire des groupes non abéliens libres » (PDF) . Journal d'algèbre . 302 (2) : 451-552. doi : 10.1016/j.jalgebra.2006.03.033 . MR  2293770 . Archivé de l'original (PDF) le 2016-10-21 . Récupéré le 04/09/2015 .
• W. Magnus, A. Karrass et D. Solitar, "Théorie des groupes combinatoires", Douvres (1976).
• PJ Higgins, 1971, "Catégories et groupoïdes", van Nostrand, {New York}. Réimpressions en théorie et applications des catégories, 7 (2005) pp 1-195.
• Sela, Zlil (2006). "La géométrie diophantienne sur les groupes. VI. La théorie élémentaire d'un groupe libre". Géom. Fonction. Anal . 16 (3) : 707-730. doi : 10.1007/s00039-006-0565-8 . MR  2238945 . S2CID  123197664 .
• Serre, Jean-Pierre , Trees , Springer (2003) (traduction anglaise de "arbres, amalgames, SL ₂ ", 3e édition, astérisque 46 (1983))
• PJ Higgins, Le groupoïde fondamental d'un graphe de groupes , Journal of the London Mathematical Society (2) 13 (1976), no. 1, 145-149.
• Aluffi, Paolo (2009). Algèbre : Chapitre 0 . Librairie AMS. p. 70. ISBN 978-0-8218-4781-7..
• Grillet, Pierre-Antoine (2007). Algèbre abstraite . Springer. p. 27. ISBN 978-0-387-71567-4..