Limite (théorie des catégories) - Limit (category theory)

Dans la théorie des catégories , une branche des mathématiques , la notion abstraite d'une limite capture les propriétés essentielles des constructions universelles telles que les produits , les retraits et les limites inverses . La notion duale de colimite généralise les constructions telles que les unions disjointes , les sommes directes , les coproduits , les poussées et les limites directes .

Les limites et les colimites, comme les notions fortement liées de propriétés universelles et de foncteurs adjoints , existent à un haut niveau d'abstraction. Afin de les comprendre, il est utile d'étudier d'abord les exemples spécifiques que ces concepts sont censés généraliser.

Définition

Les limites et colimites d'une catégorie sont définies à l'aide de diagrammes dans . Formellement, un diagramme de forme en est un foncteur de à : ${\style d'affichage C}$${\style d'affichage C}$${\style d'affichage J}$${\style d'affichage C}$${\style d'affichage J}$${\style d'affichage C}$

${\style d'affichage F:J\à C.}$

La catégorie est considérée comme une catégorie d'index , et le diagramme est considéré comme l'indexation d'une collection d'objets et de morphismes dans un motif . ${\style d'affichage J}$${\style d'affichage F}$${\style d'affichage C}$${\style d'affichage J}$

On s'intéresse le plus souvent au cas où la catégorie est une catégorie petite voire finie . Un diagramme est dit petit ou fini chaque fois qu'il l' est. ${\style d'affichage J}$${\style d'affichage J}$

Limites

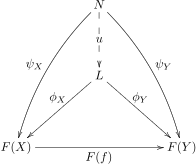
Soit un diagramme de forme dans une catégorie . Un cône à est un objet de avec une famille de morphismes indexés par les objets de , tels que pour chaque morphisme de , nous avons . ${\style d'affichage F:J\à C}$${\style d'affichage J}$${\style d'affichage C}$${\style d'affichage F}$${\style d'affichage N}$${\style d'affichage C}$${\displaystyle \psi _{X}:N\to F(X)}$${\style d'affichage X}$${\style d'affichage J}$${\style d'affichage f:X\à Y}$${\style d'affichage J}$${\displaystyle F(f)\circ \psi _{X}=\psi _{Y}}$

Une limite du diagramme est un cône à tel que pour tout autre cône à il existe un morphisme unique tel que pour tout dans . ${\style d'affichage F:J\à C}$${\style d'affichage (L,\phi )}$${\style d'affichage F}$${\style d'affichage (N,\psi )}$${\style d'affichage F}$${\displaystyle u:N\to L}$${\displaystyle \phi _{X}\circ u=\psi _{X}}$${\style d'affichage X}$${\style d'affichage J}$

On dit que le cône se factorise à travers le cône avec la factorisation unique . Le morphisme est parfois appelé le morphisme médiateur . ${\style d'affichage (N,\psi )}$${\style d'affichage (L,\phi )}$${\displaystyle u}$${\displaystyle u}$

Les limites sont également appelées cônes universels , car elles sont caractérisées par une propriété universelle (voir ci-dessous pour plus d'informations). Comme pour toute propriété universelle, la définition ci-dessus décrit un état équilibré de généralité : l'objet limite doit être suffisamment général pour permettre à n'importe quel autre cône d'en tenir compte ; d'autre part, doit être suffisamment précis, de sorte que seule une telle factorisation est possible pour chaque cône. ${\style d'affichage L}$${\style d'affichage L}$

Les limites peuvent également être caractérisées comme des objets terminaux dans la catégorie des cônes à F .

Il est possible qu'un diagramme n'ait pas de limite du tout. Cependant, si un diagramme a une limite alors cette limite est essentiellement unique : elle est unique à un isomorphisme près . Pour cette raison , on parle souvent de la limite de F .

Colimites

Les notions duales de limites et de cônes sont colimites et co-cônes. Bien qu'il soit simple d'obtenir les définitions de ceux-ci en inversant tous les morphismes dans les définitions ci-dessus, nous les énoncerons explicitement ici :

Un co-cône de schéma est un objet de collaboration avec une famille de morphisms ${\style d'affichage F:J\à C}$${\style d'affichage N}$${\style d'affichage C}$

${\displaystyle \psi _{X}:F(X)\to N}$

pour chaque objet de , tel que pour chaque morphisme dans , nous avons . ${\style d'affichage X}$${\style d'affichage J}$${\style d'affichage f:X\à Y}$${\style d'affichage J}$${\displaystyle \psi _{Y}\circ F(f)=\psi _{X}}$

Une colimite d'un diagramme est un co-cône de tel que pour tout autre co-cône de il existe un morphisme unique tel que pour tout dans . ${\style d'affichage F:J\à C}$${\style d'affichage (L,\phi )}$${\style d'affichage F}$${\style d'affichage (N,\psi )}$${\style d'affichage F}$${\displaystyle u:L\à N}$${\displaystyle u\circ \phi _{X}=\psi _{X}}$${\style d'affichage X}$${\style d'affichage J}$

Les colimites sont également appelées co-cônes universels . Ils peuvent être caractérisés comme des objets initiaux dans la catégorie des co-cônes de . ${\style d'affichage F}$

Comme pour les limites, si un diagramme a une colimite alors cette colimite est unique à un isomorphisme près. ${\style d'affichage F}$

Variantes

Des limites et des colimites peuvent également être définies pour des collections d'objets et de morphismes sans l'utilisation de diagrammes. Les définitions sont les mêmes (notez que dans les définitions ci-dessus, nous n'avons jamais eu besoin d'utiliser la composition de morphismes dans ). Cette variation n'apporte cependant aucune information nouvelle. Toute collection d'objets et de morphismes définit un graphe orienté (éventuellement grand) . Si nous laissons être la catégorie libre généré par , il y a un schéma universel dont l' image contient . La limite (ou colimite) de ce diagramme est la même que la limite (ou colimite) de la collection originale d'objets et de morphismes. ${\style d'affichage J}$ ${\style d'affichage G}$${\style d'affichage J}$${\style d'affichage G}$${\style d'affichage F:J\à C}$${\style d'affichage G}$

La limite faible et les colimites faibles sont définies comme les limites et les colimites, sauf que la propriété d'unicité du morphisme médiateur est abandonnée.

Exemples

Limites

La définition des limites est suffisamment générale pour englober plusieurs constructions utiles dans des contextes pratiques. Dans le nous considérerons en suivant la limite ( L , φ ) d'un diagramme F  : J → C .

• Objets terminaux . Si J est la catégorie vide, il n'y a qu'un seul diagramme de forme J : le vide (similaire à la fonction vide en théorie des ensembles). Un cône vers le diagramme vide n'est essentiellement qu'un objet de C . La limite de F est tout objet qui est pris en compte de manière unique par tous les autres objets. C'est juste la définition d'un objet terminal .
• Produits . Si J est une catégorie discrète alors un diagramme F n'est essentiellement rien d'autre qu'une famille d'objets de C , indexée par J . La limite L de F est appelée le produit de ces objets. Le cône φ est constitué d'une famille de morphismes φ _X  : L → F ( X ) appelés projections du produit. Dans la catégorie des ensembles , par exemple, les produits sont donnés par des produits cartésiens et les projections ne sont que les projections naturelles sur les différents facteurs.
  • Pouvoirs . Un cas particulier de produit est lorsque le diagramme F est un foncteur constant d'un objet X de C . La limite de ce schéma est appelé le J ^ième puissance de X et notée X ^J .
• Égaliseurs . Si J est une catégorie à deux objets et deux morphismes parallèles d'un objet à l'autre, alors un diagramme de forme J est une paire de morphismes parallèles dans C . La limite L d'un tel diagramme est appelée égaliseur de ces morphismes.
  • Noyaux . Un noyau est un cas particulier d'égaliseur où l'un des morphismes est un morphisme nul .
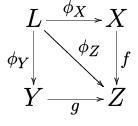
• Des retraits . Soit F un diagramme qui sélectionne trois objets X , Y et Z dans C , où les seuls morphismes de non-identité sont f  : X → Z et g  : Y → Z . La limite L de F est appelée un pullback ou un produit de fibre . Il peut très bien être visualisé sous la forme d'un carré commutatif :

• Limites inverses . Soit J un ensemble orienté (considéré comme une petite catégorie en ajoutant les flèches i → j si et seulement si i ≥ j ) et soit F  : J ^op → C un diagramme. La limite de F est appelée (de manière confuse) limite inverse ou limite projective .
• Si J = 1 , la catégorie avec un seul objet et un seul morphisme, alors un diagramme de forme J n'est essentiellement qu'un objet X de C . Un cône vers un objet X est juste un morphisme avec le codomaine X . Un morphisme f  : Y → X est une limite du diagramme X si et seulement si f est un isomorphisme . Plus généralement, si J est une catégorie quelconque avec un objet initial i , alors tout diagramme de forme J a une limite, à savoir tout objet isomorphe à F ( i ). Un tel isomorphisme détermine uniquement un cône universel à F .
• Limites topologiques . Les limites de fonctions sont un cas particulier de limites de filtres , qui sont liées aux limites catégorielles comme suit. Etant donné un espace topologique X , notons F l'ensemble des filtres sur X , x ∈ X un point, V ( x ) ∈ F le filtre de voisinage de x , A ∈ F un filtre particulier et l'ensemble des filtres plus fins que A et que converger vers x . Les filtres F sont donnés une structure de catégorie petite et mince en ajoutant une flèche A → B si et seulement si A ⊆ B . L'injection devient un foncteur et l'équivalence suivante est vérifiée :${\displaystyle F_{x,A}=\{G\in F\mid V(x)\cup A\sous-ensemble G\}}$${\displaystyle I_{x,A}:F_{x,A}\to F}$

x est une limite topologique de A si et seulement si A est une limite catégorique de${\style d'affichage I_{x,A}}$

Colimites

Des exemples de colimites sont donnés par les versions duales des exemples ci-dessus :

• Les objets initiaux sont des colimites de diagrammes vides.
• Les coproduits sont des colimites de diagrammes indexés par catégories discrètes.
  • Les copuissances sont des colimites de diagrammes constants de catégories discrètes.
• Les coégaliseurs sont des colimites d'une paire parallèle de morphismes.
  • Les conoyaux sont des coégaliseurs d'un morphisme et d'un morphisme parallèle zéro.
• Les pushouts sont les colimites d'une paire de morphismes avec un domaine commun.
• Les limites directes sont des colimites de diagrammes indexés par des ensembles dirigés.

Propriétés

Existence de limites

Un diagramme donné F  : J → C peut avoir ou non une limite (ou colimite) dans C . En effet, il se peut même qu'il n'y ait pas de cône pour F , encore moins de cône universel.

Une catégorie C est dite avoir des limites de forme J si tout diagramme de forme J a une limite dans C . Plus précisément, une catégorie C est dite

• avoir des produits s'il a des limites de forme J pour chaque petite catégorie discrète J (il n'a pas besoin d'avoir de grands produits),
• avoir des égaliseurs s'il a des limites de forme (c'est-à-dire que chaque paire parallèle de morphismes a un égaliseur),${\displaystyle \bullet \rightrightarrows \bullet }$
• avoir des pullbacks s'il a des limites de forme (c'est-à-dire que chaque paire de morphismes avec un codomaine commun a un pullback).${\displaystyle \bullet \rightarrow \bullet \leftarrow \bullet }$

Une catégorie complète est une catégorie qui a toutes les petites limites (c'est-à-dire toutes les limites de la forme J pour chaque petite catégorie J ).

On peut aussi faire les doubles définitions. Une catégorie a des colimites de forme J si chaque diagramme de forme J a une colimite dans C . Une catégorie cocomplète est celle qui a toutes les petites colimites.

Le théorème d'existence des limites stipule que si une catégorie C a des égaliseurs et tous les produits indexés par les classes Ob( J ) et Hom( J ), alors C a toutes les limites de forme J . Dans ce cas, la limite d'un diagramme F  : J → C peut être construite comme l'égaliseur des deux morphismes

${\displaystyle s,t:\prod _{i\in \operatorname {Ob} (J)}F(i)\rightrightarrows \prod _{f\in \operatorname {Hom} (J)}F(\operatorname { morue} (f))}$

donné (sous forme de composant) par

${\displaystyle {\begin{aligned}s&={\bigl (}F(f)\circ \pi _{\operatorname {dom} (f)}{\bigr )}_{f\in \operatorname {Hom} (J)}\\t&={\bigl (}\pi _{\operatorname {cod} (f)}{\bigr )}_{f\in \operatorname {Hom} (J)}.\end{aligned }}}$

Il existe un théorème d'existence double pour les colimites en termes de coégaliseurs et de coproduits. Ces deux théorèmes donnent des conditions suffisantes et nécessaires pour l'existence de toutes les (co)limites de la forme J .

Propriété universelle

Les limites et les colimites sont des cas particuliers importants de constructions universelles .

Soit C une catégorie et J une petite catégorie d'indice. La catégorie foncteur C ^J peut être considérée comme la catégorie de tous les diagrammes de forme J dans C . Le foncteur diagonal

${\displaystyle \Delta :{\mathcal {C}}\to {\mathcal {C}}^{\mathcal {J}}}$

est le foncteur qui fait correspondre chaque objet N de C au foncteur constant ( N ) : J → C à N . Autrement dit, Δ( N )( X ) = N pour chaque objet X dans J et Δ( N )( f ) = id _N pour chaque morphisme f dans J .

Étant donné un diagramme F : J → C (considéré comme un objet dans C ^J ), une transformation naturelle ψ  : Δ( N ) → F (qui n'est qu'un morphisme dans la catégorie C ^J ) est la même chose qu'un cône de N à F . Pour voir cela, notez d'abord que Δ( N )( X ) = N pour tout X implique que les composantes de ψ sont des morphismes ψ _X  : N → F ( X ), qui partagent tous le domaine N . En outre, l'exigence selon laquelle les schémas du cône font la navette est vrai simplement parce que cette ψ est une transformation naturelle. (Dualement, une transformation naturelle ψ  : F → Δ( N ) est la même chose qu'un co-cône de F vers N .)

Par conséquent, les définitions des limites et des colimites peuvent alors être reformulées sous la forme :

• Une limite de F est un morphisme universel de Δ dans F .
• Une colimite de F est un morphisme universel de F dans .

Adjonctions

Comme toutes les constructions universelles, la formation des limites et des colimites est de nature fonctionnelle. Autrement dit, si tout diagramme de forme J a une limite en C (pour J petit) il existe un foncteur limite

${\displaystyle \lim :{\mathcal {C}}^{\mathcal {J}}\to {\mathcal {C}}}$

qui attribue à chaque diagramme sa limite et à chaque transformation naturelle η : F → G l'unique morphisme lim η : lim F → lim G commutant avec les cônes universels correspondants. Ce foncteur est adjoint à droite au foncteur diagonal : C → C ^J . Cette adjonction donne une bijection entre l'ensemble de tous les morphismes de N à lim F et l'ensemble de tous les cônes de N à F

${\displaystyle \operatorname {Hom} (N,\lim F)\cong \operatorname {Cone} (N,F)}$

ce qui est naturel dans les variables N et F . L'unité de cette adjonction est simplement le cône universel de lim F à F . Si la catégorie d'indice J est connexe (et non vide) alors l'unité de l'adjonction est un isomorphisme de sorte que lim est un inverse à gauche de Δ. Cela échoue si J n'est pas connecté. Par exemple, si J est une catégorie discrète, les composantes de l'unité sont les morphismes diagonaux δ : N → N ^J .

Dualement, si tout diagramme de forme J a une colimite dans C (pour J petit) il existe un foncteur colimite

${\displaystyle \operatorname {colim} :{\mathcal {C}}^{\mathcal {J}}\to {\mathcal {C}}}$

qui attribue à chaque diagramme sa colimite. Ce foncteur est adjoint à gauche au foncteur diagonal Δ : C → C ^J , et on a un isomorphisme naturel

${\displaystyle \operatorname {Hom} (\operatorname {colim} F,N)\cong \operatorname {Cocone} (F,N).}$

L'unité de cette adjonction est le cocon universel de F au colim F . Si J est connexe (et non vide) alors la counité est un isomorphisme, de sorte que colim est un inverse à gauche de Δ.

Notez que les foncteurs limite et colimite sont des foncteurs covariants .

Comme représentations de foncteurs

On peut utiliser les foncteurs Hom pour relier les limites et colimites d'une catégorie C aux limites de Set , la catégorie des ensembles . Ceci découle, en partie, du fait que le foncteur Hom covariant Hom( N , –) : C → Set préserve toutes les limites dans C . Par dualité, le foncteur Hom contravariant doit porter les colimites aux limites.

Si un diagramme F  : J → C a une limite dans C , notée lim F , il existe un isomorphisme canonique

${\displaystyle \operatorname {Hom} (N,\lim F)\cong \lim \operatorname {Hom} (N,F-)}$

ce qui est naturel dans la variable N . Ici le foncteur Hom( N , F –) est la composition du foncteur Hom Hom( N , –) avec F . Cet isomorphisme est l'unique qui respecte les cônes limites.

On peut utiliser la relation ci-dessus pour définir la limite de F dans C . La première étape est d'observer que la limite du foncteur Hom( N , F –) peut être identifiée à l'ensemble de tous les cônes de N à F :

${\displaystyle \lim \operatorname {Hom} (N,F-)=\operatorname {Cône} (N,F).}$

Le cône limite est donné par la famille d'applications π _X  : Cone( N , F ) → Hom( N , FX ) où π _X ( ψ ) = ψ _X . Si on donne un objet L de C avec un isomorphisme naturel Φ  : Hom(–, L ) → Cone(–, F ), l'objet L sera une limite de F avec le cône limite donné par Φ _L (id _L ). En langage fantaisiste, cela revient à dire qu'une limite de F est une représentation du foncteur Cone(–, F ) : C → Set .

Dualement, si un diagramme F  : J → C a une colimite dans C , notée colim F , il existe un unique isomorphisme canonique

${\displaystyle \operatorname {Hom} (\operatorname {colim} F,N)\cong \lim \operatorname {Hom} (F-,N)}$

ce qui est naturel dans la variable N et respecte les cônes colimitants. En identifiant la limite de Hom( F –, N ) avec l'ensemble Cocone( F , N ), cette relation permet de définir la colimite du diagramme F comme représentation du foncteur Cocone( F , –).

Échange de limites et colimites d'ensembles

Soit I une catégorie finie et J une petite catégorie filtrée . Pour tout bifoncteur

${\displaystyle F:I\times J\to \mathbf {Set} ,}$

il existe un isomorphisme naturel

${\displaystyle \operatorname {colim} \limits _{J}\lim _{I}F(i,j)\rightarrow \lim _{I}\operatorname {colim} \limits _{J}F(i,j ).}$

En mots, les colimites filtrées dans Set commutent avec des limites finies. Il soutient également que les petites limites commutent avec les petites limites.

Fonctionnaires et limites

Si F  : J → C est un diagramme dans C et G  : C → D est un foncteur alors par composition (rappelons qu'un diagramme n'est qu'un foncteur) on obtient un diagramme GF  : J → D . Une question naturelle est alors :

« Comment les limites de GF sont-elles liées à celles de F ?

Préservation des limites

Un foncteur G  : C → D induit une application de Cône( F ) vers Cône( GF ) : si Ψ est un cône de N vers F alors GΨ est un cône de GN vers GF . Le foncteur G est dit à préserver les limites de F if ( GL , Gφ ) est une limite de GF chaque fois que ( L , φ ) est une limite de F . (Notez que si la limite de F n'existe pas, alors G préserve videment les limites de F .)

On dit qu'un foncteur G préserve toutes les limites de la forme J s'il préserve les limites de tous les diagrammes F  : J → C . Par exemple, on peut dire que G préserve les produits, les égaliseurs, les pullbacks, etc. Un foncteur continu est celui qui préserve toutes les petites limites.

On peut faire des définitions analogues pour les colimites. Par exemple, un foncteur G préserve les colimites de F si G ( L , φ ) est un colimite de GF chaque fois que ( L , φ ) est une colimite de F . Un foncteur cocontinu est celui qui préserve toutes les petites colimites.

Si C est une catégorie complète , alors, d'après le théorème d'existence des limites ci-dessus, un foncteur G  : C → D est continu si et seulement s'il préserve les (petits) produits et égaliseurs. Dualement, G est cocontinu si et seulement si il préserve les (petits) coproduits et coégaliseurs.

Une propriété importante des foncteurs adjoints est que tout foncteur adjoint à droite est continu et que tout foncteur adjoint à gauche est cocontinu. Comme les foncteurs adjoints existent en abondance, cela donne de nombreux exemples de foncteurs continus et cocontinus.

Pour un diagramme donné F  : J → C et le foncteur G  : C → D , si à la fois F et GF ont des limites spécifiées il existe un morphisme canonique unique

${\displaystyle \tau _{F}:G\lim F\to \lim GF}$

qui respecte les cônes limites correspondants. Le foncteur G préserve les limites de F si et seulement cette application est un isomorphisme. Si les catégories C et D ont toutes les limites de la forme J alors lim est un foncteur et les morphismes _F forment les composantes d'une transformation naturelle

${\displaystyle \tau :G\lim \to \lim G^{J}.}$

Le foncteur G préserve toutes les limites de la forme J si et seulement si τ est un isomorphisme naturel. En ce sens, on peut dire que le foncteur G commute avec des limites ( jusqu'à un isomorphisme naturel canonique).

La préservation des limites et des colimites est un concept qui ne s'applique qu'aux foncteurs covariants . Pour les foncteurs contravariants, les notions correspondantes seraient un foncteur qui prend les colimites aux limites, ou celui qui prend les limites aux colimites.

Levée des limites

Un foncteur G  : C → D est dite limite de levage pour un schéma F  : J → C si chaque fois que ( L , φ ) est une limite de GF il existe une limite ( L ', φ ') de F tel que G ( L ', φ ') = ( L , φ ). Un foncteur G lève des limites de forme J s'il lève des limites pour tous les diagrammes de forme J . On peut donc parler de produits liftants, d'égaliseurs, de pullbacks, etc. Enfin, on dit que G lifte les limites s'il lève toutes les limites. Il existe une double définition de la levée des colimites.

Un foncteur G soulève des limites uniquement pour un schéma F s'il y a un cône de pré - image uniques ( L ', φ ') de telle sorte que ( L ', φ ') est une limite de F et G ( L ', φ ') = ( L , φ ). On peut montrer que G lève les limites uniquement si et seulement s'il lève les limites et est amnésique .

La levée des limites est clairement liée à la préservation des limites. Si G lève les limites d'un diagramme F et que GF a une limite, alors F a aussi une limite et G préserve les limites de F . Il s'ensuit que :

• Si G lève les limites de toute forme J et que D a toutes les limites de la forme J , alors C a aussi toutes les limites de la forme J et G préserve ces limites.
• Si G lève toutes les petites limites et D est complet, alors C est également complet et G est continu.

Les doubles déclarations pour les colimites sont également valables.

Création et réflexion des limites

Soit F  : J → C un diagramme. Un foncteur G  : C → D est dit

• créer des limites pour F si chaque fois que ( L , φ ) est une limite de GF il existe un cône unique , ( L ', φ ') à F de telle sorte que G ( L ', φ ') = ( L , φ ) et, en outre, ce cône est une limite de F .
• reflètent les limites de F si chaque cône de F dont l'image sous G est une limite de GF est déjà une limite de F .

Duellement, on peut définir la création et la réflexion des colimites.

Les affirmations suivantes sont facilement considérées comme équivalentes :

• Le foncteur G crée des limites.
• Le foncteur G lève les limites de manière unique et reflète les limites.

Il existe des exemples de foncteurs qui lèvent des limites de manière unique mais ne les créent ni ne les reflètent.

Exemples

• Tout foncteur représentable C → Ensemble préserve les limites (mais pas nécessairement les colimites). En particulier, pour tout objet A de C , ceci est vrai du foncteur Hom covariant Hom( A ,–) : C → Set .
• Le foncteur d'oubli U  : Grp → Set crée (et préserve) toutes les petites limites et colimites filtrées ; cependant, U ne préserve pas les coproduits. Cette situation est typique des foncteurs algébriques oublieux.
• Le foncteur libre F  : Ensemble → Grp (qui assigne à tout ensemble S le groupe libre sur S ) est adjoint à gauche au foncteur oublieux U et est donc cocontinu. Ceci explique pourquoi le produit libre de deux groupes libres G et H est le groupe libre engendré par l' union disjointe des générateurs de G et H .
• Le foncteur d'inclusion Ab → Grp crée des limites mais ne préserve pas les coproduits (le coproduit de deux groupes abéliens étant la somme directe ).
• Le foncteur d'oubli Top → Set lève les limites et colimites de manière unique mais ne crée ni l'un ni l'autre.
• Soit Met _c la catégorie des espaces métriques avec des fonctions continues pour les morphismes. Le foncteur d'oubli Met _c → Set lève les limites finies mais ne les lève pas uniquement.

Une note sur la terminologie

La terminologie plus ancienne qualifiait les limites de "limites inverses" ou de "limites projectives" et les colimites de "limites directes" ou de "limites inductives". Cela a été la source de beaucoup de confusion.

Il existe plusieurs façons de se souvenir de la terminologie moderne. Tout d'abord,

• conoyaux,
• coproduits,
• coégaliseurs, et
• codomaines

sont des types de colimites, alors que

• graines,
• des produits
• égaliseurs, et
• domaines

sont des types de limites. Deuxièmement, le préfixe "co" implique "première variable du ". Des termes comme « cohomologie » et « cofibration » ont tous une association légèrement plus forte avec la première variable, c'est-à-dire la variable contravariante, du bifoncteur. ${\displaystyle \operatorname {Hom} }$${\displaystyle \operatorname {Hom} }$

Voir également

• Catégorie fermée cartésienne  – Type de catégorie en théorie des catégories
• Equalizer (mathématiques)  - Ensemble d'arguments où deux ou plusieurs fonctions ont la même valeur
• Limite inverse  – Construction en théorie des catégories
• Produit (théorie des catégories)  – Objet généralisé en théorie des catégories

Les références

• Adámek, Jiří; Horst Herrlich; George E. Strecker (1990). Catégories abstraites et concrètes (PDF) . John Wiley & Fils. ISBN 0-471-60922-6.
• Mac Lane, Saunders (1998). Catégories pour le mathématicien travaillant . Textes d'études supérieures en mathématiques . 5 (2e éd.). Springer-Verlag . ISBN 0-387-98403-8. Zbl  0906.18001 .
• Borceux, François (1994). "Limites". Manuel d'algèbre catégorielle . Encyclopédie des mathématiques et de ses applications 50-51, 53 [ie 52]. Volume 1. Cambridge University Press. ISBN 0-521-44178-1. |volume=a du texte supplémentaire ( aide )

Liens externes

• Page Web interactive qui génère des exemples de limites et de colimites dans la catégorie des ensembles finis. Écrit par Jocelyn Paine .
• Limite dans nLab