Dualité de Pontriaguine - Pontryagin duality

En mathématiques, la dualité de Pontryagin est une dualité entre des groupes abéliens localement compacts qui permet de généraliser la transformée de Fourier à tous ces groupes, qui incluent le groupe du cercle (le groupe multiplicatif des nombres complexes de module un), les groupes abéliens finis (avec la topologie discrète ) , et le groupe additif des entiers (également avec la topologie discrète), les nombres réels, et chaque espace vectoriel de dimension finie sur les réels ou un champ p -adique .

Le dual de Pontryagin d'un groupe abélien localement compact, est le groupe formé par les homomorphismes de groupe continus du groupe au groupe du cercle. Le théorème de dualité de Pontryagin établit la dualité de Pontryagin en affirmant que tout groupe abélien localement compact est naturellement isomorphe avec son bidual (le dual de son dual). Le théorème d'inversion de Fourier est un cas particulier de ce théorème.

Le sujet porte le nom de Lev Pontryagin qui a jeté les bases de la théorie des groupes abéliens localement compacts et de leur dualité au cours de ses premiers travaux mathématiques en 1934. Le traitement de Pontryagin reposait sur le fait que le groupe était dénombrable en second et compact ou discret. Cela a été amélioré pour couvrir les groupes abéliens généraux localement compacts par Egbert van Kampen en 1935 et André Weil en 1940.

introduction

La dualité de Pontryagin place dans un contexte unifié un certain nombre d'observations sur les fonctions sur la droite réelle ou sur les groupes abéliens finis :

• Les fonctions périodiques à valeurs complexes convenablement régulières sur la ligne réelle ont des séries de Fourier et ces fonctions peuvent être récupérées à partir de leur série de Fourier ;
• Les fonctions à valeurs complexes convenablement régulières sur la ligne réelle ont des transformées de Fourier qui sont également des fonctions sur la ligne réelle et, tout comme pour les fonctions périodiques, ces fonctions peuvent être récupérées à partir de leurs transformées de Fourier ; et
• Les fonctions à valeurs complexes sur un groupe abélien fini ont des transformées de Fourier discrètes , qui sont des fonctions sur le groupe dual , qui est un groupe isomorphe (non canoniquement). De plus, toute fonction sur un groupe abélien fini peut être récupérée à partir de sa transformée de Fourier discrète.

La théorie, introduite par Lev Pontryagin et combinée avec la mesure de Haar introduite par John von Neumann , André Weil et d'autres, dépend de la théorie du groupe dual d'un groupe abélien localement compact .

C'est analogue à l' espace vectoriel dual d'un espace vectoriel : un espace vectoriel de dimension finie V et son espace vectoriel dual V* ne sont pas naturellement isomorphes, mais l' algèbre d' endomorphisme (algèbre matricielle) de l'un est isomorphe à l' opposé de l'endomorphisme algèbre de l'autre : via la transposée. De même, un groupe et son groupe dual ne sont pas en général isomorphes, mais leurs anneaux d'endomorphisme sont opposés l'un à l'autre : . Plus catégoriquement, il ne s'agit pas seulement d'un isomorphisme d'algèbres d'endomorphismes, mais d'une équivalence contravariante de catégories – voir considérations catégoriques . ${\displaystyle {\text{End}}(V)\cong {{\text{End}}(V^{*})}^{\text{op}},}$${\style d'affichage G}$${\displaystyle {\widehat {G}}}$${\displaystyle {\text{End}}(G)\cong {\text{End}}({\widehat {G}})^{\text{op}}}$

Définition

Un groupe topologique est un groupe localement compact si l'espace topologique sous-jacent est localement compact et Hausdorff ; un groupe topologique est abélien si le groupe sous-jacent est abélien . Des exemples de groupes abéliens localement compacts comprennent les groupes abéliens finis, les entiers (tous deux pour la topologie discrète , qui est également induite par la métrique habituelle), les nombres réels, le groupe de cercles T (tous deux avec leur topologie métrique habituelle), et aussi le nombres p -adiques (avec leur topologie p -adique habituelle ).

Pour un groupe abélien localement compact , le dual de Pontryagin est le groupe des homomorphismes de groupe continus du groupe du cercle . C'est-à-dire, ${\style d'affichage G}$${\displaystyle {\widehat {G}}}$${\style d'affichage G}$${\style d'affichage T}$

${\displaystyle {\widehat {G}}:=\operatorname {Hom} (G,T).}$

Le dual de Pontryagin est généralement doté de la topologie donnée par la convergence uniforme sur les ensembles compacts (c'est-à-dire la topologie induite par la topologie compacte-ouverte sur l'espace de toutes les fonctions continues de à ). ${\displaystyle {\widehat {G}}}$${\style d'affichage G}$${\style d'affichage T}$

Par exemple,

${\displaystyle {\widehat {\mathbb {Z} }}=T,\ {\widehat {\mathbb {R} }}=\mathbb {R} ,\ {\widehat {T}}=\mathbb {Z} .}$

Le théorème de dualité de Pontryagin

Théorème : Il existe un isomorphisme canonique   entre tout groupe abélien localement compact et son double dual.${\displaystyle G\cong {\widehat {\widehat {G}}}}$${\style d'affichage G}$

Canonique signifie qu'il existe une carte naturellement définie  ; plus important encore, la carte doit être fonctionnelle au format . L'isomorphisme canonique est défini comme suit : ${\displaystyle \operatorname {ev} _{G}\colon G\to {\widehat {\widehat {G}}}}$${\style d'affichage G}$${\displaystyle \operatorname {ev} _{G}}$${\style d'affichage x\dans G}$

${\displaystyle \operatorname {ev} _{G}(x)(\chi )=\chi (x)\in \mathbb {T} .\ {\text{ C'est-à-dire }}\ \operatorname {ev} _ {G}(x):(\chi \mapsto \chi (x)).}$

En d'autres termes, chaque élément de groupe est identifié au caractère d'évaluation sur le dual. Ceci est fortement analogue à l' isomorphisme canonique entre un espace vectoriel de dimension finie et son double dual , , et il convient de mentionner que tout espace vectoriel est un groupe abélien . Si est un groupe abélien fini, alors mais cet isomorphisme n'est pas canonique. Préciser (en général) cette affirmation nécessite de penser à dualisation non seulement sur les groupes, mais aussi sur les cartes entre les groupes, afin de traiter la dualisation comme un foncteur et prouver que le foncteur identité et le foncteur de dualisation ne sont pas naturellement équivalents. De plus, le théorème de dualité implique que pour tout groupe (pas nécessairement fini) le foncteur de dualisation est un foncteur exact. ${\style d'affichage x}$${\displaystyle V\cong V^{**}}$${\style d'affichage V}$${\style d'affichage G}$${\displaystyle G\cong {\widehat {G}}}$

Dualité de Pontriaguine et transformée de Fourier

Mesure de Haar

L'un des faits les plus remarquables à propos d'un groupe localement compact est qu'il porte une mesure naturelle essentiellement unique , la mesure de Haar , qui permet de mesurer de manière cohérente la "taille" de sous-ensembles suffisamment réguliers de . "Sous-ensemble suffisamment régulier" signifie ici un ensemble de Borel ; c'est-à-dire un élément de la -algèbre générée par les ensembles compacts . Plus précisément, une mesure de Haar à droite sur un groupe localement compact est une mesure dénombrable additive définie sur les ensembles de Borel dont l' invariant à droite au sens où μ( Ax ) = μ( A ) pour un élément de et un sous-ensemble de Borel de et satisfait également à certaines conditions de régularité (décrites en détail dans l'article sur la mesure de Haar ). À l'exception des facteurs d'échelle positifs, une mesure de Haar sur est unique. ${\style d'affichage G}$${\style d'affichage G}$${\style d'affichage G}$${\style d'affichage G}$${\style d'affichage x}$${\style d'affichage G}$${\style d'affichage A}$${\style d'affichage G}$${\style d'affichage G}$

La mesure de Haar sur nous permet de définir la notion d' intégrale pour les fonctions boréliennes (à valeurs complexes ) définies sur le groupe. En particulier, on peut considérer différents espaces L ^p associés à la mesure de Haar . Spécifiquement, ${\style d'affichage G}$

${\displaystyle {\mathcal {L}}_{\mu }^{p}(G)=\left\{(f:G\to \mathbb {C} )\ {\Big |}\ \int _{ G}|f(x)|^{p}\ d\mu (x)<\infty \right\}.}$

Notez que, puisque deux mesures de Haar sur sont égales à un facteur d'échelle près, cet espace est indépendant du choix de la mesure de Haar et pourrait donc peut-être être écrit sous la forme . Cependant, la norme sur cet espace dépend du choix de la mesure de Haar, donc si l'on veut parler d'isométries, il est important de garder une trace de la mesure de Haar utilisée. ${\style d'affichage G}$${\displaystyle L^{p}}$${\style d'affichage L^{p}(G)}$${\displaystyle L^{p}}$

Transformée de Fourier et de la formule d'inversion de Fourier pour L ¹ -functions

Le groupe dual d'un groupe abélien localement compact est utilisé comme espace sous-jacent pour une version abstraite de la transformée de Fourier . Si , alors la transformée de Fourier est la fonction sur définie par ${\displaystyle f\in L^{1}(G)}$${\displaystyle {\widehat {f}}}$${\displaystyle {\widehat {G}}}$

${\displaystyle {\widehat {f}}(\chi )=\int _{G}f(x){\overline {\chi (x)}}\ d\mu (x),}$

où l'intégrale est relative à la mesure de Haar sur . Ceci est également noté . Notez que la transformée de Fourier dépend du choix de la mesure de Haar. Il n'est pas trop difficile de montrer que la transformée de Fourier d'une fonction sur est une fonction continue bornée sur laquelle s'annule à l'infini . ${\style d'affichage \mu }$${\style d'affichage G}$${\displaystyle ({\mathcal {F}}f)(\chi )}$${\style d'affichage L^{1}}$${\style d'affichage G}$${\displaystyle {\widehat {G}}}$

Formule d'inversion de Fourier pour les fonctions. ${\style d'affichage L^{1}}$Pour chaque mesure de Haar sur il y a une mesure de Haar unique sur telle que chaque fois et , nous avons ${\style d'affichage \mu }$${\style d'affichage G}$${\style d'affichage \nu }$${\displaystyle {\widehat {G}}}$${\displaystyle f\in L^{1}(G)}$${\displaystyle {\widehat {f}}\in L^{1}\left({\widehat {G}}\right)}$

${\displaystyle f(x)=\int _{\widehat {G}}{\widehat {f}}(\chi )\chi (x)\ d\nu (\chi )\qquad \mu {\text{ -presque partout}}}$

Si est continue alors cette identité est valable pour tout .${\style d'affichage f}$${\style d'affichage x}$

La transformée de Fourier inverse d'une fonction intégrable sur est donnée par ${\displaystyle {\widehat {G}}}$

${\displaystyle {\check {g}}(x)=\int _{\widehat {G}}g(\chi )\chi (x)\ d\nu (\chi ),}$

où l'intégrale est relative à la mesure de Haar sur le groupe dual . La mesure sur qui apparaît dans la formule d'inversion de Fourier est appelée la double mesure à et peut être notée . ${\style d'affichage \nu }$${\displaystyle {\widehat {G}}}$${\style d'affichage \nu }$${\displaystyle {\widehat {G}}}$${\style d'affichage \mu }$${\displaystyle {\widehat {\mu }}}$

Les différentes transformations de Fourier peuvent être classées en fonction de leur domaine et domaine de transformation (le groupe et le groupe dual) comme suit (notez qu'il s'agit du groupe Circle ): ${\displaystyle \mathbb {T} }$

Transformer	Domaine d'origine, ${\style d'affichage G}$	Transformer le domaine, ${\displaystyle {\hat {G}}}$	Mesure, ${\style d'affichage \mu }$
transformée de Fourier	${\displaystyle \mathbb {R} }$	${\displaystyle \mathbb {R} }$	${\displaystyle {\text{Constant}}\times {\text{Mesure de Lebesgue}}}$
série de Fourier	${\displaystyle \mathbb {T} }$	${\displaystyle \mathbb {Z} }$	${\displaystyle {\text{Constant}}\times {\text{Mesure de Lebesgue}}}$
Transformée de Fourier en temps discret (DTFT)	${\displaystyle \mathbb {Z} }$	${\displaystyle \mathbb {T} }$	${\displaystyle {\text{Constant}}\times {\text{Mesure de comptage}}}$
Transformée de Fourier discrète (DFT)	${\displaystyle \mathbb {Z} _{n}}$	${\displaystyle \mathbb {Z} _{n}}$	${\displaystyle {\text{Constant}}\times {\text{Mesure de comptage}}}$

A titre d'exemple, supposons que , donc nous pouvons penser que par l'appariement Si est la mesure de Lebesgue sur l'espace euclidien, nous obtenons la transformée de Fourier ordinaire sur et la mesure duale nécessaire pour la formule d'inversion de Fourier est . Si nous voulons obtenir une formule d'inversion de Fourier avec la même mesure des deux côtés (c'est-à-dire que nous pouvons considérer comme son propre espace dual, nous pouvons demander à égal à ) alors nous devons utiliser ${\displaystyle G=\mathbb {R} ^{n}}$${\displaystyle {\widehat {G}}}$${\displaystyle \mathbb {R} ^{n}}$${\displaystyle (\mathbf {v} ,\mathbf {w} )\mapsto e^{i\mathbf {v} \cdot \mathbf {w} }.}$${\style d'affichage \mu }$${\displaystyle \mathbb {R} ^{n}}$${\displaystyle {\widehat {\mu }}=(2\pi )^{-n}\mu }$${\displaystyle \mathbb {R} ^{n}}$${\displaystyle {\widehat {\mu }}}$${\style d'affichage \mu }$

${\displaystyle {\begin{aligned}\mu &=(2\pi )^{-{\frac {n}{2}}}\times {\text{Mesure de Lebesgue}}\\{\widehat {\mu }}&=(2\pi )^{-{\frac {n}{2}}}\times {\text{Mesure de Lebesgue}}\end{aligned}}}$

Cependant, si nous changeons la façon dont nous nous identifions à son groupe dual, en utilisant l'appariement ${\displaystyle \mathbb {R} ^{n}}$

${\displaystyle (\mathbf {v} ,\mathbf {w} )\mapsto e^{2\pi i\mathbf {v} \cdot \mathbf {w} },}$

alors la mesure de Lebesgue sur est égale à sa propre mesure duale . Cette convention minimise le nombre de facteurs qui apparaissent à divers endroits lors du calcul des transformées de Fourier ou des transformées de Fourier inverses sur l'espace euclidien. (En effet, il limite le seul à l'exposant plutôt qu'à un pré-facteur en dehors du signe intégral.) Notez que le choix de la façon de s'identifier avec son groupe dual affecte la signification du terme « fonction auto-duale », qui est une fonction égale à sa propre transformée de Fourier : en utilisant l'appariement classique, la fonction est auto-duale. Mais l'utilisation de l'appariement, qui maintient le préfacteur comme unité, rend l' auto-dualité à la place. Cette deuxième définition de la transformée de Fourier a l'avantage de faire correspondre l'identité multiplicative à l'identité de convolution, ce qui est utile comme l' est une algèbre de convolution. Voir la section suivante sur l'algèbre de groupe . De plus, cette forme est aussi nécessairement isométrique sur les espaces. Voir ci-dessous les théorèmes d'inversion de Plancherel et L ^{2 de} Fourier${\displaystyle \mathbb {R} ^{n}}$${\style d'affichage 2\pi }$${\style d'affichage 2\pi }$${\displaystyle \mathbb {R} ^{n}}$${\displaystyle \mathbb {R} ^{n}}$${\displaystyle (\mathbf {v} ,\mathbf {w} )\mapsto e^{i\mathbf {v} \cdot \mathbf {w} }}$${\displaystyle e^{-{\frac {1}{2}}x^{2}}}$${\displaystyle (\mathbf {v} ,\mathbf {w} )\mapsto e^{2\pi {i}{\mathbf {v} }\cdot {\mathbf {w} }}}$${\displaystyle e^{-\pi x^{2}}}$${\style d'affichage L^{1}}$${\style d'affichage L^{2}}$

L'algèbre de groupe

L'espace des fonctions intégrables sur un groupe abélien localement compact est une algèbre , où la multiplication est convolution : la convolution de deux fonctions intégrables et est définie comme ${\style d'affichage G}$${\style d'affichage f}$${\style d'affichage g}$

${\displaystyle (f*g)(x)=\int _{G}f(xy)g(y)\ d\mu (y).}$

Théorème. L'espace de Banach est une algèbre associative et commutative sous convolution.${\style d'affichage L^{1}(G)}$

Cette algèbre est appelée algèbre de groupe de . D'après le théorème de Fubini-Tonelli , la convolution est sous-multiplicative par rapport à la norme, ce qui en fait une algèbre de Banach . L'algèbre de Banach a un élément d'identité multiplicatif si et seulement si est un groupe discret, à savoir la fonction qui est 1 à l'identité et zéro ailleurs. En général, cependant, il a une identité approximative qui est un réseau (ou séquence généralisée) indexé sur un ensemble dirigé tel que${\style d'affichage G}$${\style d'affichage L^{1}}$${\style d'affichage L^{1}(G)}$${\style d'affichage L^{1}(G)}$${\style d'affichage G}$${\displaystyle \{e_{i}\}_{i\in I}}$${\style d'affichage I}$${\displaystyle f*e_{i}\to f.}$

La transformée de Fourier amène la convolution à la multiplication, c'est-à-dire qu'il s'agit d'un homomorphisme d'algèbres de Banach abéliennes (de norme ≤ 1) : ${\displaystyle L^{1}(G)\to C_{0}\left({\widehat {G}}\right)}$

${\displaystyle {\mathcal {F}}(f*g)(\chi )={\mathcal {F}}(f)(\chi )\cdot {\mathcal {F}}(g)(\chi ) .}$

En particulier, à chaque caractère de groupe correspond une unique fonctionnelle linéaire multiplicative sur l'algèbre des groupes définie par ${\style d'affichage G}$

${\displaystyle f\mapsto {\widehat {f}}(\chi ).}$

C'est une propriété importante de l'algèbre de groupe que celles-ci épuisent l'ensemble des fonctionnelles linéaires multiplicatives non triviales (c'est-à-dire pas identiquement zéro) sur l'algèbre de groupe ; voir l'article 34 de ( Loomis 1953 ). Cela signifie que la transformée de Fourier est un cas particulier de la transformée de Gelfand .

Théorèmes d'inversion de Plancherel et L ² Fourier

Comme nous l'avons dit, le groupe dual d'un groupe abélien localement compact est un groupe abélien localement compact à part entière et a donc une mesure de Haar, ou plus précisément toute une famille de mesures de Haar d'échelle.

Théorème. Choisissez une mesure Haar sur et laissez être la double mesure sur comme défini ci-dessus. Si est continue à support compact alors et ${\style d'affichage \mu }$${\style d'affichage G}$${\style d'affichage \nu }$${\displaystyle {\widehat {G}}}$${\displaystyle f:G\to \mathbb {C} }$${\displaystyle {\widehat {f}}\in L^{2}\left({\widehat {G}}\right)}$

${\displaystyle \int _{G}|f(x)|^{2}\ d\mu (x)=\int _{\widehat {G}}\left|{\widehat {f}}(\chi )\right|^{2}\ d\nu (\chi ).}$

En particulier, la transformée de Fourier est une isométrie des fonctions continues à valeurs complexes de support compact sur les -fonctions sur (en utilisant la -norme par rapport à μ pour les fonctions sur et la -norme par rapport à ν pour les fonctions sur ).${\style d'affichage L^{2}}$${\style d'affichage G}$${\style d'affichage L^{2}}$${\displaystyle {\widehat {G}}}$${\style d'affichage L^{2}}$${\style d'affichage G}$${\style d'affichage L^{2}}$${\displaystyle {\widehat {G}}}$

Puisque les fonctions continues à valeurs complexes du support compact sur sont -denses, il existe une extension unique de la transformée de Fourier de cet espace à un opérateur unitaire${\style d'affichage G}$${\style d'affichage L^{2}}$

${\displaystyle {\mathcal {F}}:L_{\mu }^{2}(G)\to L_{\nu }^{2}\left({\widehat {G}}\right).}$

et on a la formule

${\displaystyle \forall f\in L^{2}(G):\quad \int _{G}|f(x)|^{2}\ d\mu (x)=\int _{\widehat { G}}\left|{\widehat {f}}(\chi )\right|^{2}\ d\nu (\chi ).}$

Notez que pour les groupes localement compacts non compacts, l'espace ne contient pas , donc la transformée de Fourier des fonctions générales sur n'est "pas" donnée par n'importe quel type de formule d'intégration (ou vraiment n'importe quelle formule explicite). Pour définir la transformée de Fourier, il faut recourir à une astuce technique telle que partir d'un sous-espace dense comme les fonctions continues à support compact puis étendre l'isométrie par continuité à tout l'espace. Cette extension unitaire de la transformée de Fourier est ce que nous entendons par transformée de Fourier sur l'espace des fonctions carrées intégrables. ${\style d'affichage G}$${\style d'affichage L^{1}(G)}$${\style d'affichage L^{2}(G)}$${\style d'affichage L^{2}}$${\style d'affichage G}$${\style d'affichage L^{2}}$

Le groupe dual possède également une transformée de Fourier inverse à part entière ; il peut être caractérisé comme l'inverse (ou adjoint, puisqu'il est unitaire) de la transformée de Fourier. C'est le contenu de la formule d'inversion de Fourier qui suit. ${\style d'affichage L^{2}}$${\style d'affichage L^{2}}$

Théorème. L'adjointe de la transformée de Fourier restreinte aux fonctions continues de support compact est la transformée de Fourier inverse

${\displaystyle L_{\nu }^{2}\left({\widehat {G}}\right)\to L_{\mu }^{2}(G)}$

où est la double mesure de .${\style d'affichage \nu }$${\style d'affichage \mu }$

Dans le cas où le groupe dual est naturellement isomorphe au groupe des entiers et la transformée de Fourier est spécialisée dans le calcul de coefficients de séries de Fourier de fonctions périodiques. ${\displaystyle G=\mathbb {T} }$${\displaystyle {\widehat {G}}}$${\displaystyle \mathbb {Z} }$

Si est un groupe fini, on retrouve la transformée de Fourier discrète . Notez que ce cas est très facile à prouver directement. ${\style d'affichage G}$

Compactification de Bohr et quasi-périodicité

Une application importante de la dualité de Pontryagin est la caractérisation suivante des groupes topologiques abéliens compacts :

Théorème . Un groupe abélien localement compact est compact si et seulement si le groupe dual est discret. Inversement, est discret si et seulement si est compact.${\style d'affichage G}$${\displaystyle {\widehat {G}}}$${\style d'affichage G}$${\displaystyle {\widehat {G}}}$

Qu'être compact implique qu'il soit discret ou qu'être discret implique qu'il soit compact est une conséquence élémentaire de la définition de la topologie compacte-ouverte sur et n'a pas besoin de la dualité de Pontryagin. On utilise la dualité de Pontriaguine pour prouver l'inverse. ${\style d'affichage G}$${\displaystyle {\widehat {G}}}$${\style d'affichage G}$${\displaystyle {\widehat {G}}}$${\displaystyle {\widehat {G}}}$

La compactification de Bohr est définie pour tout groupe topologique , qu'il soit localement compact ou abélien. Une utilisation faite de la dualité de Pontryagin entre groupes abéliens compacts et groupes abéliens discrets est de caractériser la compactification de Bohr d'un groupe topologique abélien localement compact arbitraire . La compactification de Bohr de est , où H a la structure de groupe , mais étant donné la topologie discrète . Depuis la carte d'inclusion${\style d'affichage G}$${\style d'affichage G}$ ${\style d'affichage B(G)}$${\style d'affichage G}$${\displaystyle {\widehat {H}}}$${\displaystyle {\widehat {G}}}$

${\displaystyle \iota :H\to {\widehat {G}}}$

est continue et un homomorphisme, le morphisme dual

${\displaystyle G\sim {\widehat {\widehat {G}}}\to {\widehat {H}}}$

est un morphisme en un groupe compact dont il est facile de montrer qu'il satisfait la propriété universelle requise .

Voir aussi fonction presque périodique .

Considérations catégorielles

La dualité de Pontriaguine peut aussi être envisagée avec profit sur le plan fonctionnel . Dans ce qui suit, l' ACV est la catégorie des groupes abéliens localement compacts et des homomorphismes de groupes continus. La construction du groupe dual de est un foncteur contravariant LCA → LCA , représenté (au sens des foncteurs représentables ) par le groupe du cercle comme En particulier, le double foncteur dual est covariant . Une formulation catégorique de la dualité de Pontryagin indique alors que la transformation naturelle entre le foncteur identité sur ACV et le double foncteur dual est un isomorphisme. Déroulant la notion de transformation naturelle, cela signifie que les applications sont des isomorphismes pour tout groupe abélien localement compact , et ces isomorphismes sont fonctionnels dans . Cet isomorphisme est analogue au double dual des espaces vectoriels de dimension finie (un cas particulier, pour les espaces vectoriels réels et complexes). ${\displaystyle {\widehat {G}}}$${\displaystyle \mathbb {T} }$${\displaystyle {\widehat {G}}={\text{Hom}}(G,\mathbb {T} ).}$${\displaystyle G\to {\widehat {\widehat {G}}}}$${\displaystyle G\to \operatorname {Hom} (\operatorname {Hom} (G,T),T)}$${\style d'affichage G}$${\style d'affichage G}$

Une conséquence immédiate de cette formulation est une autre formulation catégorielle commune de la dualité de Pontryagin : le foncteur de groupe dual est une équivalence de catégories de l' ACV à l' ACV ^op .

La dualité échange les sous-catégories de groupes discrets et de groupes compacts . Si est un anneau et est à gauche - le module , le groupe dual deviendra un droit -module; de cette façon, nous pouvons également voir que les modules discrets à gauche seront des modules Pontryagin dual à compacts à droite . L'anneau des endomorphismes dans l' ACV est changé par dualité en son anneau opposé (changer la multiplication dans l'autre ordre). Par exemple, si est un groupe discret cyclique infini, est un groupe circulaire : le premier a donc cela est vrai aussi du second. ${\style d'affichage R}$${\style d'affichage G}$${\style d'affichage R}$${\displaystyle {\widehat {G}}}$${\style d'affichage R}$${\style d'affichage R}$${\style d'affichage R}$${\displaystyle {\text{Fin}}(G)}$${\style d'affichage G}$${\displaystyle {\widehat {G}}}$${\displaystyle {\text{Fin}}(G)=\mathbb {Z} }$

Généralisations

Les généralisations de la dualité de Pontryagin sont construites dans deux directions principales : pour les groupes topologiques commutatifs qui ne sont pas localement compacts , et pour les groupes topologiques non commutatifs. Les théories dans ces deux cas sont très différentes.

Dualités pour les groupes topologiques commutatifs

Quand est un groupe topologique abélien de Hausdorff, le groupe avec la topologie compacte-ouverte est un groupe topologique abélien de Hausdorff et la cartographie naturelle de son double-dual a un sens. Si cette application est un isomorphisme, on dit que satisfait la dualité de Pontryagin (ou c'est un groupe réflexif , ou un groupe réflexif ). Ceci a été étendu dans un certain nombre de directions au-delà du cas qui est localement compact. ${\style d'affichage G}$${\displaystyle {\widehat {G}}}$${\style d'affichage G}$${\displaystyle {\widehat {\widehat {G}}}}$${\style d'affichage G}$${\style d'affichage G}$${\style d'affichage G}$

En particulier, Samuel Kaplan a montré en 1948 et 1950 que les produits arbitraires et les limites inverses dénombrables de groupes abéliens localement compacts (Hausdorff) satisfont la dualité de Pontryagin. Notez qu'un produit infini d'espaces non compacts localement compacts n'est pas localement compact.

Plus tard, en 1975, Rangachari Venkataraman montra, entre autres faits, que tout sous-groupe ouvert d'un groupe topologique abélien qui satisfait la dualité de Pontriaguine satisfait lui-même la dualité de Pontriaguine.

Plus récemment, Sergio Ardanza-Trevijano et María Jesús Chasco ont étendu les résultats de Kaplan mentionnés ci-dessus. Ils ont montré que les limites directes et inverses des suites de groupes abéliens satisfaisant la dualité de Pontryagin satisfont également la dualité de Pontryagin si les groupes sont métrisables ou -espaces mais pas nécessairement localement compacts, à condition que certaines conditions supplémentaires soient satisfaites par les suites. ${\displaystyle k_{\omega }}$

Cependant, il y a un aspect fondamental qui change si l'on veut considérer la dualité de Pontryagin au-delà du cas localement compact. Elena Martín-Peinador a prouvé en 1995 que if est un groupe topologique abélien de Hausdorff qui satisfait la dualité de Pontryagin, et l'appariement naturel d'évaluation ${\style d'affichage G}$

${\displaystyle {\begin{cases}G\times {\widehat {G}}\to \mathbb {T} \\(x,\chi )\mapsto \chi (x)\end{cases}}}$

est (conjointement) continue, puis est localement compacte. En corollaire, tous les exemples non localement compacts de dualité de Pontryagin sont des groupes où l'appariement n'est pas (conjointement) continu. ${\style d'affichage G}$${\displaystyle G\times {\widehat {G}}\to \mathbb {T} }$

Une autre façon de généraliser la dualité de Pontryagin à des classes plus larges de groupes topologiques commutatifs est de doter le groupe dual d'une topologie un peu différente, à savoir la topologie de convergence uniforme sur des ensembles totalement bornés . Les groupes satisfaisant l'identité sous cette hypothèse sont appelés groupes stéréotypés . Cette classe est également très large (et elle contient des groupes abéliens localement compacts), mais elle est plus étroite que la classe des groupes réfléchissants. ${\displaystyle {\widehat {G}}}$${\displaystyle G\cong {\widehat {\widehat {G}}}}$

Dualité de Pontryagin pour les espaces vectoriels topologiques

En 1952, Marianne F. Smith remarqua que les espaces de Banach et les espaces réflexifs , étant considérés comme des groupes topologiques (avec l'opération de groupe additif), satisfont à la dualité de Pontryagin. Plus tard BS Brudovskiĭ, William C. Waterhouse et K. Brauner ont montré que ce résultat peut être étendu à la classe de tous les espaces tonnelés quasi-complets (en particulier, à tous les espaces de Fréchet ). Dans les années 1990, Sergei Akbarov a décrit la classe des espaces vectoriels topologiques qui satisfont à une propriété plus forte que la réflexivité classique de Pontryagin, à savoir l'identité

${\displaystyle (X^{\star })^{\star }\cong X}$

où , l'espace de l' ensemble des fonctionnelles linéaires continus muni de la topologie de la convergence uniforme sur des ensembles totalement délimitées dans (et des moyens pour le double dans le même sens). Les espaces de cette classe sont appelés espaces stéréotypés , et la théorie correspondante a trouvé une série d'applications en analyse fonctionnelle et en géométrie, y compris la généralisation de la dualité de Pontryagin pour les groupes topologiques non commutatifs. ${\displaystyle X^{\star }}$${\displaystyle f\colon X\to {\mathbb {C} }}$${\style d'affichage X}$${\style d'affichage (X^{\star })^{\star }}$${\displaystyle X^{\star }}$

Dualités pour les groupes topologiques non commutatifs

Pour les groupes localement compacts non commutatifs, la construction classique de Pontryagin cesse de fonctionner pour diverses raisons, notamment parce que les caractères ne séparent pas toujours les points de , et les représentations irréductibles de ne sont pas toujours unidimensionnelles. En même temps, il n'est pas clair comment introduire la multiplication sur l'ensemble des représentations unitaires irréductibles de , et il n'est même pas clair si cet ensemble est un bon choix pour le rôle de l'objet dual pour . Ainsi, le problème de la construction de la dualité dans cette situation nécessite une refonte complète. ${\style d'affichage G}$${\style d'affichage G}$${\style d'affichage G}$${\style d'affichage G}$${\style d'affichage G}$

Les théories construites à ce jour sont divisées en deux groupes principaux : les théories où l'objet duel a la même nature que l'objet source (comme dans la dualité de Pontryagin elle-même), et les théories où l'objet source et son double diffèrent l'un de l'autre si radicalement qu'il est impossible de les compter comme des objets d'une même classe.

Les théories du deuxième type étaient historiquement les premières : peu de temps après les travaux de Pontryagin, Tadao Tannaka (1938) et Mark Kerin (1949) ont construit une théorie de la dualité pour des groupes compacts arbitraires connue maintenant sous le nom de dualité Tannaka-Krein . Dans cette théorie, l'objet dual d'un groupe n'est pas un groupe mais une catégorie de ses représentations . ${\style d'affichage G}$ ${\style d'affichage \Pi (G)}$

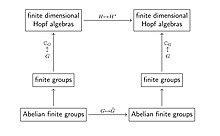
Les théories du premier type sont apparues plus tard et l'exemple clé pour elles était la théorie de la dualité pour les groupes finis. Dans cette théorie, la catégorie des groupes finis est intégrée par l'opération consistant à prendre l' algèbre des groupes (sur ) dans la catégorie des algèbres de Hopf de dimension finie , de sorte que le foncteur de dualité de Pontryagin se transforme en l'opération consistant à prendre l' espace vectoriel dual (qui est une dualité foncteur dans la catégorie des algèbres de Hopf de dimension finie). ${\displaystyle G\mapsto {\mathbb {C} }_{G}}$ ${\displaystyle {\mathbb {C} }_{G}}$${\displaystyle {\mathbb {C} }}$${\displaystyle G\mapsto {\widehat {G}}}$${\displaystyle H\mapsto H^{*}}$

En 1973, Leonid I. Vainerman, George I. Kac, Michel Enock et Jean-Marie Schwartz ont construit une théorie générale de ce type pour tous les groupes localement compacts. A partir des années 1980, les recherches dans ce domaine ont repris après la découverte des groupes quantiques , auxquels les théories construites ont commencé à être activement transférées. Ces théories sont formulées dans le langage des C*-algèbres , ou algèbres de Von Neumann , et l'une de ses variantes est la théorie récente des groupes quantiques localement compacts .

L'un des inconvénients de ces théories générales, cependant, est qu'en elles les objets généralisant le concept de groupe ne sont pas des algèbres de Hopf au sens algébrique habituel. Cette déficience peut être corrigée (pour certaines classes de groupes) dans le cadre de théories de la dualité construites à partir de la notion d' enveloppe de l'algèbre topologique.

Voir également

• Théorème de Peter-Weyl
• La dualité Cartier
• Espace stéréotype

Remarques

Les références

• Dixmier, Jacques (1969). Les C*-algèbres et leurs représentations . Gauthier-Villars. ISBN 978-2-87647-013-2.
• Enock, Michel ; Schwartz, Jean-Marie (1992). Algèbres de Kac et dualité des groupes localement compacts . Avec une préface d'Alain Connes. Avec une postface d'Adrian Ocneanu. Berlin : Springer-Verlag. doi : 10.1007/978-3-662-02813-1 . ISBN 978-3-540-54745-7. MR  1215933 .
• Hewitt, Edwin ; Ross, Kenneth A. (1963). Analyse harmonique abstraite. Vol. I : Structure des groupes topologiques. Théorie de l'intégration, représentations de groupe . Die Grundlehren der mathematischen Wissenschaften. 115 . Berlin-Göttingen-Heidelberg : Springer-Verlag. ISBN 978-0-387-94190-5. MR  0156915 .
• Hewitt, Edwin ; Ross, Kenneth A. (1970). Analyse harmonique abstraite . 2 . ISBN 978-3-662-24595-8. MR  0262773 .
• Kirillov, Alexandre A. (1976) [1972]. Éléments de la théorie des représentations . Grundlehren der Mathematischen Wissenschaften. 220 . Berlin, New York : Springer-Verlag . ISBN 978-0-387-07476-4. MR  0412321 .
• Loomis, Lynn H. (1953). Une introduction à l'analyse harmonique abstraite . D. van Nostrand Co. ISBN 978-0486481234.
• Morris, SA (1977). Dualité de Pontryagin et structure des groupes abéliens localement compacts . Presse de l'Université de Cambridge . ISBN 978-0521215435.
• Onishchik, AL (1984). Dualité de Pontrjaguine . Encyclopédie des mathématiques . 4 . p. 481-482. ISBN 978-1402006098.
• Reiter, Hans (1968). Analyse harmonique classique et groupes localement compacts . ISBN 978-0198511892.
• Rudin, Walter (1962). Analyse de Fourier sur les groupes . D. van Nostrand Co. ISBN 978-0471523642.
• Timmermann, T. (2008). Une invitation aux groupes quantiques et à la dualité - des algèbres de Hopf aux unitaires multiplicatifs et au-delà . EMS Textbooks in Mathematics, European Mathematical Society. ISBN 978-3-03719-043-2.
• Kustermans, J.; Vaes, S. (2000). « Groupes quantiques localement compacts » . Annales Scientifiques de l'École Normale Supérieure . 33 (6) : 837-934. doi : 10.1016/s0012-9593(00)01055-7 .
• Ardanza-Trevijano, Sergio; Chasco, Maria Jesús (2005). « La dualité de Pontryagin des limites séquentielles des groupes abéliens topologiques ». Journal d'algèbre pure et appliquée . 202 (1–3) : 11–21. doi : 10.1016/j.jpaa.2005.02.006 . hdl : 10171/1586 . MR  2163398 .
• Chasco, Maria Jesús; Dikranjan, Dikran; Martín-Peinador, Elena (2012). « Une enquête sur la réflexivité des groupes topologiques abéliens » . Topologie et ses applications . 159 (9) : 2290–2309. doi : 10.1016/j.topol.2012.04.012 . MR  2921819 .
• Kaplan, Samuel (1948). "Extensions de la dualité Pontrjagin. Partie I: produits infinis". Journal mathématique du duc . 15 : 649-658. doi : 10.1215/S0012-7094-48-01557-9 . MR  0026999 .
• Kaplan, Samuel (1950). "Extensions de la dualité de Pontrjagin. Partie II: limites directes et inverses". Journal mathématique du duc . 17 : 419-435. doi : 10.1215/S0012-7094-50-01737-6 . MR  0049906 .
• Venkataraman, Rangachari (1975). "Les extensions de la dualité de Pontryagin". Mathematische Zeitschrift . 143 (2) : 105-112. doi : 10.1007/BF01187051 . S2CID  123627326 .
• Martin-Peinador, Elena (1995). « Un groupe topologique admissible réflexible doit être localement compact ». Actes de la Société mathématique américaine . 123 (11) : 3563-3566. doi : 10.2307/2161108 . hdl : 10338.dmlcz/127641 . JSTOR  2161108 .
• Smith, Marianne F. (1952). « Le théorème de dualité de Pontrjagin dans les espaces linéaires ». Annales de mathématiques . 56 (2) : 248-253. doi : 10.2307/1969798 . JSTOR  1969798 . MR  0049479 .
• Brudovskiĭ, BS (1967). « Sur k- et c-réflexivité des espaces vectoriels localement convexes ». Journal mathématique lituanien . 7 (1) : 17-21.
• Waterhouse, William C. (1968). "Deux groupes d'espaces vectoriels" . Journal Pacifique de Mathématiques . 26 (1) : 193-196. doi : 10.2140/pjm.1968.26.193 .
• Brauner, Kalman (1973). « Duels d'espaces de Fréchet et une généralisation du théorème de Banach-Dieudonné ». Journal mathématique du duc . 40 (4) : 845-855. doi : 10.1215/S0012-7094-73-04078-7 .
• Akbarov, SS (2003). « Dualité de Pontryagin dans la théorie des espaces vectoriels topologiques et en algèbre topologique ». Journal des sciences mathématiques . 113 (2) : 179-349. doi : 10.1023/A:1020929201133 . S2CID  115297067 .
• Akbarov, Sergueï S. ; Shavgulidze, Evgeniy T. (2003). « Sur deux classes d'espaces réflexifs au sens de Pontryagin » . Matematicheskii Sbornik . 194 (10) : 3-26.
• Akbarov, Sergueï S. (2009). « Fonctions holomorphes de type exponentiel et dualité pour les groupes de Stein avec composante algébrique connexe de l' identité ». Journal des sciences mathématiques . 162 (4) : 459-586. arXiv : 0806.3205 . doi : 10.1007/s10958-009-9646-1 . S2CID  115153766 .
• Akbarov, Sergueï S. (2017). "Enveloppes continues et lisses d'algèbres topologiques. Partie 1". Journal des sciences mathématiques . 227 (5) : 531-668. arXiv : 1303.2424 . doi : 10.1007/s10958-017-3599-6 . MR  3790317 . S2CID  126018582 .
• Akbarov, Sergueï S. (2017). "Enveloppes continues et lisses d'algèbres topologiques. Partie 2". Journal des sciences mathématiques . 227 (6) : 669-789. arXiv : 1303.2424 . doi : 10.1007/s10958-017-3600-4 . MR  3796205 . S2CID  128246373 .