Bivecteur - Bivector

En mathématiques , un bivecteur ou 2-vecteur est une quantité en algèbre extérieure ou algèbre géométrique qui étend l'idée de scalaires et de vecteurs . Si un scalaire est considéré comme une quantité de degré zéro et qu'un vecteur est une quantité de degré un, alors un bivecteur peut être considéré comme étant de degré deux. Les bivecteurs ont des applications dans de nombreux domaines des mathématiques et de la physique. Ils sont liés aux nombres complexes en deux dimensions et à la fois aux pseudovecteurs et aux quaternions en trois dimensions. Ils peuvent être utilisés pour générer des rotations dans n'importe quel nombre de dimensions et sont un outil utile pour classer ces rotations. Ils sont également utilisés en physique , liant ensemble un certain nombre de quantités autrement sans rapport.

Les bivecteurs sont générés par le produit extérieur sur les vecteurs : étant donné deux vecteurs a et b , leur produit extérieur a ∧ b est un bivecteur, tout comme la somme de tous les bivecteurs. Tous les bivecteurs ne peuvent pas être générés comme un seul produit extérieur. Plus précisément, un bivecteur qui peut être exprimé comme un produit extérieur est dit simple ; jusqu'à trois dimensions, tous les bivecteurs sont simples, mais dans les dimensions supérieures, ce n'est pas le cas. Le produit extérieur de deux vecteurs est alternée , de sorte que b ∧ une est la négation de la bivecteur un ∧ b , produisant l'orientation opposée, et un ∧ un est le bivecteur zéro.

Géométriquement, un simple bivecteur peut être interprété comme un segment plan orienté , tout comme les vecteurs peuvent être considérés comme des segments de ligne orientés . Le bivecteur a ∧ b a une amplitude égale à l'aire du parallélogramme avec les arêtes a et b , a l' attitude du plan couvert par a et b , et a l' orientation étant le sens de la rotation qui alignerait a avec b .

En termes simples, toute surface est le même bivecteur, si elle a la même aire, la même orientation et est parallèle au même plan (voir figure).

Histoire

Le bivecteur a été défini pour la première fois en 1844 par le mathématicien allemand Hermann Grassmann en algèbre extérieure comme le résultat du produit extérieur de deux vecteurs. Rien que l'année précédente, en Irlande, William Rowan Hamilton avait découvert des quaternions . Ce n'est que lorsque le mathématicien anglais William Kingdon Clifford en 1888 a ajouté le produit géométrique à l'algèbre de Grassmann, incorporant les idées de Hamilton et Grassmann, et a fondé l' algèbre de Clifford , que le bivecteur tel qu'il est connu aujourd'hui a été pleinement compris.

À cette époque, Josiah Willard Gibbs et Oliver Heaviside ont développé le calcul vectoriel , qui comprenait des produits croisés et des produits scalaires distincts dérivés de la multiplication des quaternions. Le succès du calcul vectoriel et du livre Vector Analysis de Gibbs et Wilson , a eu pour effet que les idées de Hamilton et Clifford ont été négligées pendant longtemps, car une grande partie des mathématiques et de la physique du 20e siècle a été formulée en termes vectoriels. Gibbs a utilisé des vecteurs pour remplir le rôle de bivecteurs en trois dimensions, et a utilisé « bivecteur » pour décrire une quantité sans rapport, une utilisation qui a parfois été copiée. Aujourd'hui , le bivecteur est largement étudié comme sujet dans l' algèbre géométrique , une algèbre de Clifford sur réelles ou complexes espaces vectoriels avec une forme quadratique . Sa résurgence a été dirigée par David Hestenes qui, avec d'autres, a appliqué l'algèbre géométrique à une gamme de nouvelles applications en physique .

Dérivation

Pour cet article, le bivecteur ne sera considéré que dans les algèbres géométriques réelles. Dans la pratique, ce n'est pas vraiment une restriction, car toutes les applications utiles sont tirées de ces algèbres. De plus, sauf indication contraire, tous les exemples ont une métrique euclidienne et donc une forme quadratique définie positive .

Algèbre géométrique et produit géométrique

Le bivecteur résulte de la définition du produit géométrique sur un espace vectoriel. Pour les vecteurs a , b et c , le produit géométrique sur les vecteurs est défini comme suit :

L'associativité

${\displaystyle (\mathbf {ab} )\mathbf {c} =\mathbf {a} (\mathbf {bc} )}$

Distributivité gauche et droite

${\displaystyle {\begin{aligné}\mathbf {a} (\mathbf {b} +\mathbf {c} )&=\mathbf {ab} +\mathbf {ac} \\(\mathbf {b} +\ mathbf {c} )\mathbf {a} &=\mathbf {ba} +\mathbf {ca} \end{aligné}}}$

Contraction

${\displaystyle {\mathbf {a} }^{2}=Q(\mathbf {a} )=\epsilon _{\mathbf {a} }{\left|\mathbf {a} \right|}^{2 }}$

Où Q est la forme quadratique, | un | est la grandeur de a et ϵ _a est la signature métrique . Pour un espace avec une métrique euclidienne ϵ _a est 1 donc peut être omis, et la condition de contraction devient :

${\displaystyle {\mathbf {a} }^{2}={\left|\mathbf {a} \right|}^{2}}$

Le produit intérieur

D'après l'associativité, a ( ab ) = a ² b , a fois scalaire b . Lorsque b n'est pas parallèle et n'est donc pas un multiple scalaire de a , ab ne peut pas être un scalaire. Mais

${\displaystyle {\frac {1}{2}}(\mathbf {ab} +\mathbf {ba} )={\frac {1}{2}}\left((\mathbf {a} +\mathbf { b} )^{2}-\mathbf {a} ^{2}-\mathbf {b} ^{2}\right)}$

est une somme de scalaires et donc un scalaire. D'après la loi des cosinus sur le triangle formé par les vecteurs sa valeur est | un | | b | cos  θ , où θ est l'angle entre les vecteurs. Il est donc identique au produit intérieur entre deux vecteurs, et s'écrit de la même manière,

${\displaystyle \mathbf {a} \cdot \mathbf {b} ={\frac {1}{2}}(\mathbf {ab} +\mathbf {ba} ).}$

Il est symétrique, de valeur scalaire, et peut être utilisé pour déterminer l'angle entre deux vecteurs : en particulier si a et b sont orthogonaux le produit est nul.

Le produit extérieur

De même que le produit intérieur peut être formulé comme la partie symétrique du produit géométrique d'une autre quantité, le produit extérieur (parfois appelé produit "coin" ou "progressif") peut être formulé comme sa partie antisymétrique :

${\displaystyle \mathbf {a} \wedge \mathbf {b} ={\frac {1}{2}}(\mathbf {ab} -\mathbf {ba} )}$

Il est antisymétrique en a et b

${\displaystyle \mathbf {b} \wedge \mathbf {a} ={\frac {1}{2}}(\mathbf {ba} -\mathbf {ab} )=-{\frac {1}{2} }(\mathbf {ab} -\mathbf {ba} )=-\mathbf {a} \wedge \mathbf {b} }$

et par addition :

${\displaystyle \mathbf {a} \cdot \mathbf {b} +\mathbf {a} \wedge \mathbf {b} ={\frac {1}{2}}(\mathbf {ab} +\mathbf {ba } )+{\frac {1}{2}}(\mathbf {ab} -\mathbf {ba} )=\mathbf {ab} }$

C'est-à-dire que le produit géométrique est la somme du produit intérieur symétrique et du produit extérieur antisymétrique.

Pour examiner la nature de a ∧ b , considérons la formule

${\displaystyle (\mathbf {a} \cdot \mathbf {b} )^{2}-(\mathbf {a} \wedge \mathbf {b} )^{2}=\mathbf {a} ^{2} \mathbf {b} ^{2},}$

qui en utilisant l' identité trigonométrique de Pythagore donne la valeur de ( a ∧ b ) ²

${\displaystyle (\mathbf {a} \wedge \mathbf {b} )^{2}=(\mathbf {a} \cdot \mathbf {b} )^{2}-\mathbf {a} ^{2} \mathbf {b} ^{2}=\gauche|\mathbf {a} \right|^{2}\gauche|\mathbf {b} \right|^{2}(\cos ^{2}\theta - 1)=-\left|\mathbf {a} \right|^{2}\left|\mathbf {b} \right|^{2}\sin ^{2}\theta }$

Avec un carré négatif, il ne peut pas s'agir d'une quantité scalaire ou vectorielle, c'est donc une nouvelle sorte d'objet, un bivecteur . Il a de l' ampleur | un | | b | | sin  & thetav | Où θ est l'angle entre les vecteurs, et ainsi est égal à zéro pour les vecteurs parallèles.

Pour les distinguer des vecteurs, les bivecteurs s'écrivent ici avec des majuscules en gras, par exemple :

${\displaystyle \mathbf {A} =\mathbf {a} \wedge \mathbf {b} =-\mathbf {b} \wedge \mathbf {a} \ ,}$

bien que d'autres conventions soient utilisées, en particulier car les vecteurs et les bivecteurs sont tous deux des éléments de l'algèbre géométrique.

Propriétés

L'espace ² R ⁿ

L'algèbre générée par le produit géométrique est l' algèbre géométrique sur l'espace vectoriel. Pour un espace vectoriel euclidien, il s'écrit ou Cl _n ( R ), où n est la dimension de l'espace vectoriel R ⁿ . Cl _n ( R ) est à la fois un espace vectoriel et une algèbre, généré par tous les produits entre vecteurs dans R ⁿ , il contient donc tous les vecteurs et bivecteurs. Plus précisément en tant qu'espace vectoriel, il contient les vecteurs et les bivecteurs sous forme de sous - espaces linéaires , mais pas de sous-algèbres (puisque le produit géométrique de deux vecteurs n'est généralement pas un autre vecteur). L'espace de tous les bivecteurs s'écrit ⋀ ² R ⁿ . ${\displaystyle {\mathcal {G}}_{n}}$

La sous-algèbre paire

La sous-algèbre générée par les bivecteurs est la sous-algèbre paire de l'algèbre géométrique, notée Cl⁺
_n( R ). Cette algèbre résulte de la considération de tous les produits de scalaires et de bivecteurs générés par le produit géométrique. Il a pour dimension 2 ^{n −1} , et contient ⋀ ² R ⁿ comme un sous-espace linéaire de dimension 1/2n ( n − 1) (un nombre triangulaire ). En deux et trois dimensions, la sous-algèbre paire ne contient que des scalaires et des bivecteurs, et chacun présente un intérêt particulier. En deux dimensionsla même sousalgèbre est isomorphe aux nombres complexes , C , alors que dans troisil est isomorphe au quaternions , H . Plus généralement, la sous-algèbre paire peut être utilisée pour générer des rotations dans n'importe quelle dimension, et peut être générée par des bivecteurs dans l'algèbre.

Ordre de grandeur

Comme indiqué dans la section précédente, la grandeur d'un bivecteur simple, c'est-à-dire le produit extérieur de deux vecteurs a et b , est | un | | b | sin θ , où θ est l'angle entre les vecteurs. C'est écrit | B |, où B est le bivecteur.

Pour les bivecteurs généraux, la grandeur peut être calculée en prenant la norme du bivecteur considéré comme un vecteur dans l'espace ⋀ ² R ⁿ . Si la magnitude est nulle, alors toutes les composantes du bivecteur sont nulles et le bivecteur est le bivecteur nul qui, en tant qu'élément de l'algèbre géométrique, est égal au zéro scalaire.

Bivecteurs unitaires

Un bivecteur unitaire est un bivecteur de grandeur unitaire. Il peut être dérivé de n'importe quel bivecteur non nul en divisant le bivecteur par sa magnitude, c'est-à-dire

${\displaystyle {\frac {\mathbf {B} }{\left|\mathbf {B} \right|}}.}$

Les bivecteurs unitaires formés à partir des produits de la base standard sont particulièrement intéressants . Si e _i et e _j sont des vecteurs de base distincts alors le produit e _i ∧ e _j est un bivecteur. Comme les vecteurs sont orthogonaux c'est juste e _i e _j , noté e _ij , avec une unité de grandeur car les vecteurs sont des vecteurs unitaires . L'ensemble de tous ces bivecteurs forme une base pour ⋀ ² R ⁿ . Par exemple, en quatre dimensions, la base de ⋀ ² R ⁴ est ( e ₁ e ₂ , e ₁ e ₃ , e ₁ e ₄ , e ₂ e ₃ , e ₂ e ₄ , e ₃ e ₄ ) ou ( e ₁₂ , e ₁₃ , e ₁₄ , e ₂₃ , e ₂₄ , e ₃₄ ).

Bivecteurs simples

Le produit extérieur de deux vecteurs est un bivecteur, mais tous les bivecteurs ne sont pas des produits extérieurs de deux vecteurs. Par exemple, en quatre dimensions le bivecteur

${\displaystyle \mathbf {B} =\mathbf {e} _{1}\wedge \mathbf {e} _{2}+\mathbf {e} _{3}\wedge \mathbf {e} _{4} =\mathbf {e} _{1}\mathbf {e} _{2}+\mathbf {e} _{3}\mathbf {e} _{4}=\mathbf {e} _{12}+\ mathbf {e} _{34}}$

ne peut pas être écrit comme le produit extérieur de deux vecteurs. Un bivecteur qui peut être écrit comme le produit extérieur de deux vecteurs est simple. En deux et trois dimensions, tous les bivecteurs sont simples, mais pas en quatre dimensions ou plus ; en quatre dimensions, chaque bivecteur est la somme d'au plus deux produits extérieurs. Un bivecteur a un vrai carré si et seulement s'il est simple, et seuls les bivecteurs simples peuvent être représentés géométriquement par une aire plane orientée.

Produit de deux bivecteurs

Le produit géométrique de deux bivecteurs, A et B , est

${\displaystyle \mathbf {A} \mathbf {B} =\mathbf {A} \cdot \mathbf {B} +\mathbf {A} \times \mathbf {B} +\mathbf {A} \wedge \mathbf { B} .}$

La quantité A ⋅ B est le produit intérieur d'une valeur scalaire, tandis que A ∧ B est le produit de grade 4 de l' extérieur qui se pose en quatre dimensions ou plus. La quantité A × B est le produit du commutateur à valeur bivecteur , donné par

${\displaystyle \mathbf {A} \times \mathbf {B} ={\frac {1}{2}}(\mathbf {AB} -\mathbf {BA} ),}$

L'espace des bivecteurs ⋀ ² R ⁿ est une algèbre de Lie sur R , avec le produit du commutateur comme parenthèse de Lie. Le produit géométrique complet des bivecteurs génère la sous-algèbre paire.

Le produit d'un bivecteur avec lui-même est particulièrement intéressant. Comme le produit du commutateur est antisymétrique, le produit se simplifie en

${\displaystyle \mathbf {A} \mathbf {A} =\mathbf {A} \cdot \mathbf {A} +\mathbf {A} \wedge \mathbf {A} .}$

Si le bivecteur est simple , le dernier terme est nul et le produit est le scalaire valeur A ⋅ A , qui peut être utilisé comme un chèque de simplicité. En particulier, le produit extérieur des bivecteurs n'existe qu'en quatre dimensions ou plus, donc tous les bivecteurs en deux et trois dimensions sont simples.

Deux dimensions

Lorsque l'on travaille avec des coordonnées en algèbre géométrique, il est habituel d'écrire les vecteurs de base sous la forme ( e ₁ , e ₂ , ...), une convention qui sera utilisée ici.

Un vecteur dans l'espace réel à deux dimensions R ² peut être écrit a = a ₁ e ₁ + a ₂ e ₂ , où a ₁ et a ₂ sont des nombres réels, e ₁ et e ₂ sont des vecteurs de base orthonormés . Le produit géométrique de deux de ces vecteurs est

${\displaystyle {\begin{aligned}\mathbf {a} \mathbf {b} &=(a_{1}\mathbf {e} _{1}+a_{2}\mathbf {e} _{2}) (b_{1}\mathbf {e} _{1}+b_{2}\mathbf {e} _{2})\\&=a_{1}b_{1}\mathbf {e} _{1} \mathbf {e} _{1}+a_{1}b_{2}\mathbf {e} _{1}\mathbf {e} _{2}+a_{2}b_{1}\mathbf {e} _{2}\mathbf {e} _{1}+a_{2}b_{2}\mathbf {e} _{2}\mathbf {e} _{2}\\&=a_{1}b_{ 1}+a_{2}b_{2}+(a_{1}b_{2}-a_{2}b_{1})\mathbf {e} _{1}\mathbf {e} _{2}. \end{aligné}}}$

Cela peut être divisé en un produit intérieur symétrique à valeur scalaire et un produit extérieur antisymétrique à valeur bivecteur :

${\displaystyle {\begin{aligned}\mathbf {a} \cdot \mathbf {b} &=a_{1}b_{1}+a_{2}b_{2},\\\mathbf {a} \wedge \mathbf {b} &=(a_{1}b_{2}-a_{2}b_{1})\mathbf {e} _{1}\mathbf {e} _{2}=(a_{1} b_{2}-a_{2}b_{1})\mathbf {e} _{12}.\end{aligned}}}$

Tous les bivecteurs en deux dimensions sont de cette forme, c'est-à-dire des multiples du bivecteur e ₁ e ₂ , noté e ₁₂ pour souligner qu'il s'agit d'un bivecteur plutôt que d'un vecteur. La magnitude de e ₁₂ est 1, avec

${\displaystyle \mathbf {e} _{12}^{2}=-1,}$

on l'appelle donc l' unité bivecteur . Le terme unité bivecteur peut être utilisé dans d'autres dimensions mais il n'est défini de manière unique (au signe près) qu'en deux dimensions et tous les bivecteurs sont des multiples de e ₁₂ . Comme l'élément de plus haut grade de l'algèbre e ₁₂ est également le pseudoscalaire qui reçoit le symbole i .

Nombres complexes

Avec les propriétés du carré négatif et l' ampleur de l' unité, l'unité bivecteur peut être identifiée à l' unité imaginaire de nombres complexes . Les bivecteurs et les scalaires forment ensemble la sous-algèbre paire de l'algèbre géométrique, qui est isomorphe aux nombres complexes C . La sous-algèbre paire a une base (1, e ₁₂ ), toute l'algèbre a une base (1, e ₁ , e ₂ , e ₁₂ ).

Les nombres complexes sont généralement identifiés aux axes de coordonnées et aux vecteurs bidimensionnels, ce qui reviendrait à les associer aux éléments vectoriels de l'algèbre géométrique. Il n'y a pas de contradiction à cela, car pour passer d'un vecteur général à un nombre complexe, un axe doit être identifié comme l'axe réel, disons e ₁ . Cela se multiplie par tous les vecteurs pour générer les éléments de même sous-algèbre.

Toutes les propriétés des nombres complexes peuvent être dérivées des bivecteurs, mais deux sont particulièrement intéressantes. D'abord comme avec les nombres complexes les produits de bivecteurs et donc la sous-algèbre paire sont commutatives . Cela n'est vrai qu'en deux dimensions, de sorte que les propriétés du bivecteur en deux dimensions qui dépendent de la commutativité ne se généralisent généralement pas aux dimensions supérieures.

Deuxièmement, un bivecteur général peut être écrit

${\displaystyle \theta \mathbf {e} _{12}=i\theta ,}$

où θ est un nombre réel. Mettre ceci dans la série de Taylor pour la carte exponentielle et utiliser la propriété e ₁₂ ² = −1 donne une version bivecteur de la formule d' Euler ,

${\displaystyle e^{\theta \mathbf {e} _{12}}=e^{i\theta }=\cos {\theta }+i\sin {\theta },}$

qui , lorsqu'il est multiplié par tout vecteur tourne à travers un angle θ autour de l'origine:

${\displaystyle (x'\mathbf {e} _{1}+y'\mathbf {e} _{2})=(x\mathbf {e} _{1}+y\mathbf {e} _{2 })e^{i\thêta }.}$

Le produit d'un vecteur avec un bivecteur en deux dimensions est anticommutatif , donc les produits suivants génèrent tous la même rotation

${\displaystyle \mathbf {v} '=\mathbf {v} e^{i\theta }=e^{-i\theta }\mathbf {v} =e^{\frac {-i\theta }{2 }}\mathbf {v} e^{\frac {i\theta }{2}}.}$

Parmi ceux-ci, le dernier produit est celui qui se généralise dans des dimensions supérieures. La quantité nécessaire est appelée rotor et est donné le symbole R , donc en deux dimensions d' un rotor qui tourne à travers l' angle θ peuvent être écrits

${\displaystyle R=e^{\frac {-i\theta }{2}}=e^{\frac {-\theta \mathbf {e} _{12}}{2}},}$

et la rotation qu'il génère est

${\displaystyle \mathbf {v} '=R\mathbf {v} R^{-1}.\,}$

Trois dimensions

En trois dimensions, le produit géométrique de deux vecteurs est

${\displaystyle {\begin{aligned}\mathbf {ab} &=(a_{1}\mathbf {e} _{1}+a_{2}\mathbf {e} _{2}+a_{3}\ mathbf {e} _{3})(b_{1}\mathbf {e} _{1}+b_{2}\mathbf {e} _{2}+b_{3}\mathbf {e} _{3 })\\&=a_{1}b_{1}{\mathbf {e} _{1}}^{2}+a_{2}b_{2}{\mathbf {e} _{2}}^ {2}+a_{3}b_{3}{\mathbf {e} _{3}}^{2}+(a_{2}b_{3}-a_{3}b_{2})\mathbf { e} _{2}\mathbf {e} _{3}+(a_{3}b_{1}-a_{1}b_{3})\mathbf {e} _{3}\mathbf {e} _ {1}+(a_{1}b_{2}-a_{2}b_{1})\mathbf {e} _{1}\mathbf {e} _{2}.\end{aligned}}}$

Cela peut être divisé en produit intérieur symétrique à valeur scalaire et produit extérieur antisymétrique à valeur bivecteur :

${\displaystyle {\begin{aligned}\mathbf {a} \cdot \mathbf {b} &=a_{1}b_{1}+a_{2}b_{2}+a_{3}b_{3}\ \\mathbf {a} \wedge \mathbf {b} &=(a_{2}b_{3}-a_{3}b_{2})\mathbf {e} _{23}+(a_{3}b_ {1}-a_{1}b_{3})\mathbf {e} _{31}+(a_{1}b_{2}-a_{2}b_{1})\mathbf {e} _{12 }.\end{aligné}}}$

En trois dimensions tous les bivecteurs sont simples et donc le résultat d'un produit extérieur. Les bivecteurs unitaires e ₂₃ , e ₃₁ et e ₁₂ forment une base pour l'espace des bivecteurs ² R ³ , qui est lui-même un espace linéaire tridimensionnel. Donc si un bivecteur général est :

${\displaystyle \mathbf {A} =A_{23}\mathbf {e} _{23}+A_{31}\mathbf {e} _{31}+A_{12}\mathbf {e} _{12} ,}$

ils peuvent être ajoutés comme des vecteurs

${\displaystyle \mathbf {A} +\mathbf {B} =(A_{23}+B_{23})\mathbf {e} _{23}+(A_{31}+B_{31})\mathbf { e} _{31}+(A_{12}+B_{12})\mathbf {e} _{12}.}$

tandis que lorsqu'ils sont multipliés, ils produisent ce qui suit

${\displaystyle \mathbf {A} \mathbf {B} =-A_{23}B_{23}-A_{31}B_{31}-A_{12}B_{12}+(A_{12}B_{31 }-A_{31}B_{12})\mathbf {e} _{23}+(A_{23}B_{12}-A_{12}B_{23})\mathbf {e} _{31}+ (A_{31}B_{23}-A_{23}B_{31})\mathbf {e} _{12}}$

qui peut être divisé en parties scalaires symétriques et bivecteurs antisymétriques comme suit

${\displaystyle {\begin{aligned}\mathbf {A} \cdot \mathbf {B} &=-A_{12}B_{12}-A_{31}B_{31}-A_{23}B_{23} \\\mathbf {A} \times \mathbf {B} &=(A_{23}B_{31}-A_{31}B_{23})\mathbf {e} _{12}+(A_{12} B_{23}-A_{23}B_{12})\mathbf {e} _{13}+(A_{31}B_{12}-A_{12}B_{31})\mathbf {e} _{ 23}.\end{aligned}}}$

Le produit extérieur de deux bivecteurs en trois dimensions est nul.

Un bivecteur B peut être écrit comme le produit de sa magnitude et d'un bivecteur unitaire, écrivant donc β pour | B | et en utilisant la série de Taylor pour la carte exponentielle, on peut montrer que

${\displaystyle e^{\mathbf {B} }=e^{\beta {\frac {\mathbf {B} }{\beta }}}=\cos {\beta }+{\frac {\mathbf {B } }{\beta }}\sin {\beta }.}$

C'est une autre version de la formule d'Euler, mais avec un bivecteur général en trois dimensions. Contrairement à deux dimensions, les bivecteurs ne sont pas commutatifs, donc les propriétés qui dépendent de la commutativité ne s'appliquent pas à trois dimensions. Par exemple, en général , e ^{A + B} ≠ e ^A e ^B en trois (ou plus) dimensions.

L'algèbre géométrique complète en trois dimensions, Cl ₃ ( R ), a pour base (1, e ₁ , e ₂ , e ₃ , e ₂₃ , e ₃₁ , e ₁₂ , e ₁₂₃ ). L'élément e ₁₂₃ est un trivecteur et le pseudoscalaire pour la géométrie. Les bivecteurs en trois dimensions sont parfois identifiés avec des pseudovecteurs auxquels ils sont liés, comme discuté ci-dessous .

quaternions

Les bivecteurs ne sont pas fermés sous le produit géométrique, mais la sous-algèbre paire l'est. En trois dimensions, il se compose de tous les éléments scalaires et bivecteurs de l'algèbre géométrique, donc un élément général peut être écrit par exemple a + A , où a est la partie scalaire et A est la partie bivecteur. Il est écrit Cl⁺
₃et a une base (1, e ₂₃ , e ₃₁ , e ₁₂ ). Le produit de deux éléments généraux de la sous-algèbre paire est

${\displaystyle (a+\mathbf {A} )(b+\mathbf {B} )=ab+a\mathbf {B} +b\mathbf {A} +\mathbf {A} \cdot \mathbf {B} +\ mathbf {A} \times \mathbf {B} .}$

La sous-algèbre paire, c'est-à-dire l'algèbre constituée de scalaires et de bivecteurs, est isomorphe aux quaternions , H . Ceci peut être vu en comparant la base à la base du quaternion, ou à partir du produit ci-dessus qui est identique au produit du quaternion, à l'exception d'un changement de signe qui concerne les produits négatifs dans le produit bivecteur intérieur A ⋅ B . D'autres propriétés des quaternions peuvent être liées ou dérivées de l'algèbre géométrique.

Cela suggère que la division habituelle d'un quaternion en parties scalaire et vectorielle serait mieux représentée comme une division en parties scalaire et bivecteur ; si cela est fait, le produit de quaternion est simplement le produit géométrique. Il relie également les quaternions en trois dimensions aux nombres complexes en deux, car chacun est isomorphe à la sous-algèbre paire pour la dimension, une relation qui se généralise aux dimensions supérieures.

Vecteur de rotation

Le vecteur de rotation, à partir de la représentation axe-angle des rotations, est une manière compacte de représenter les rotations en trois dimensions. Dans sa forme la plus compacte, il est constitué d'un vecteur, le produit d'un vecteur unitaire ω qui est l' axe de rotation avec le (signé) angle de rotation θ , de sorte que l'amplitude du vecteur global de rotation θω est égale à la (unsigned) angle de rotation.

Le quaternion associé à la rotation est

${\displaystyle q=\left(\cos \left({\frac {\theta }{2}}\right),\omega \sin \left({\frac {\theta }{2}}\right)\ droit)}$

En algèbre géométrique, la rotation est représentée par un bivecteur. Cela peut être vu dans sa relation avec les quaternions. Soit Ω un bivecteur unitaire dans le plan de rotation, et soit θ l' angle de rotation . Alors le bivecteur de rotation est Ω θ . Le quaternion correspond étroitement à l'exponentielle de la moitié du bivecteur Ω θ . C'est-à-dire que les composantes du quaternion correspondent aux parties scalaire et bivecteur de l'expression suivante :

L'exponentielle peut être définie en termes de sa série de puissances, et facilement évaluée en utilisant le fait que Ω au carré est -1.

Les rotations peuvent donc être représentées par des bivecteurs. Tout comme les quaternions sont des éléments de l'algèbre géométrique, ils sont liés par la carte exponentielle de cette algèbre.

Rotors

Le bivecteur Ohm & thetav génère une rotation de la carte exponentielle. Les éléments pairs générés font tourner un vecteur général en trois dimensions de la même manière que les quaternions :

Comme en deux dimensions, la quantité e ^{- Ω θ /2} est appelée un rotor et notée R . La quantité e ^{Ohm & thetav / 2} est alors R ^-1 , et ils génèrent des rotations que

Ceci est identique à deux dimensions, sauf qu'ici les rotors sont des objets à quatre dimensions isomorphes aux quaternions. Ceci peut être généralisé à toutes les dimensions, avec des rotors, éléments de la sous-algèbre paire de grandeur unitaire, étant générés par la carte exponentielle des bivecteurs. Ils forment une double couverture sur le groupe de rotation, de sorte que les rotors R et − R représentent la même rotation.

Matrices

Les bivecteurs sont des matrices isomorphes à antisymétriques ; le bivecteur général B ₂₃ e ₂₃ + B ₃₁ e ₃₁ + B ₁₂ e ₁₂ correspond à la matrice

${\displaystyle M_{B}={\begin{pmatrix}0&B_{12}&-B_{31}\\-B_{12}&0&B_{23}\\B_{31}&-B_{23}&0\end {pmatrice}}.}$

Ceci multiplié par des vecteurs des deux côtés donne le même vecteur que le produit d'un vecteur et d'un bivecteur moins le produit extérieur; un exemple est le tenseur de vitesse angulaire .

Les matrices symétriques asymétriques génèrent des matrices orthogonales avec le déterminant 1 à travers la carte exponentielle. En particulier, l'exposant d'un bivecteur associé à une rotation est une matrice de rotation , c'est-à-dire que la matrice de rotation M _R donnée par la matrice antisymétrique ci-dessus est

${\displaystyle M_{R}=e^{M_{B}}.}$

La rotation décrite par M _R est la même que celle décrite par le rotor R donnée par

${\displaystyle R=e^{\frac {B}{2}},}$

et la matrice M _R peut aussi être calculée directement à partir du rotor R :

${\displaystyle M_{R}={\begin{pmatrix}(R\mathbf {e} _{1}R^{-1})\cdot \mathbf {e} _{1}&(R\mathbf {e } _{2}R^{-1})\cdot \mathbf {e} _{1}&(R\mathbf {e} _{3}R^{-1})\cdot \mathbf {e} _ {1}\\(R\mathbf {e} _{1}R^{-1})\cdot \mathbf {e} _{2}&(R\mathbf {e} _{2}R^{- 1})\cdot \mathbf {e} _{2}&(R\mathbf {e} _{3}R^{-1})\cdot \mathbf {e} _{2}\\(R\mathbf {e} _{1}R^{-1})\cdot \mathbf {e} _{3}&(R\mathbf {e} _{2}R^{-1})\cdot \mathbf {e } _{3}&(R\mathbf {e} _{3}R^{-1})\cdot \mathbf {e} _{3}\end{pmatrix}}.}$

Les bivecteurs sont liés aux valeurs propres d'une matrice de rotation. Étant donné une matrice de rotation M, les valeurs propres peuvent être calculées en résolvant l' équation caractéristique de cette matrice 0 = det( M − λ I ) . D'après le théorème fondamental de l'algèbre, cela a trois racines (dont une seule est réelle car il n'y a qu'un seul vecteur propre, c'est-à-dire l'axe de rotation). Les autres racines doivent être une paire conjuguée complexe. Ils ont des grandeurs unitaires donc des logarithmes purement imaginaires, égales à la grandeur du bivecteur associé à la rotation, qui est aussi l'angle de rotation. Les vecteurs propres associés aux valeurs propres complexes sont dans le plan du bivecteur, de sorte que le produit extérieur de deux vecteurs propres non parallèles donne le bivecteur (ou un multiple de celui-ci).

Vecteurs axiaux

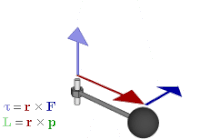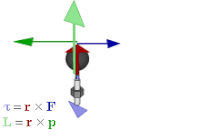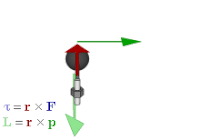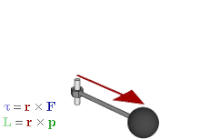
Le vecteur rotation est un exemple de vecteur axial . Les vecteurs axiaux, ou pseudovecteurs, sont des vecteurs avec la particularité que leurs coordonnées subissent un changement de signe par rapport aux vecteurs habituels (également appelés "vecteurs polaires") lors d'une inversion par l'origine, d'une réflexion dans un plan ou d'une autre transformation linéaire d'inversion d'orientation. . Les exemples incluent des quantités comme le couple , le moment angulaire et les champs magnétiques vectoriels . Les quantités qui utiliseraient des vecteurs axiaux en algèbre vectorielle sont correctement représentées par des bivecteurs en algèbre géométrique. Plus précisément, si une orientation sous-jacente est choisie, les vecteurs axiaux s'identifient naturellement aux vecteurs usuels ; le dual de Hodge donne alors l'isomorphisme entre vecteurs axiaux et bivecteurs, donc chaque vecteur axial est associé à un bivecteur et vice versa ; C'est

${\displaystyle \mathbf {A} =*\mathbf {a} \,,\quad \mathbf {a} =*\mathbf {A} }$

où indique le dual de Hodge. Notez que si l'orientation sous-jacente est inversée par inversion par l'origine, l'identification des vecteurs axiaux avec les vecteurs habituels et le double signe de Hodge changent, mais les bivecteurs ne bougent pas. Alternativement, en utilisant l' unité pseudoscalaire dans Cl ₃ ( R ), i = e ₁ e ₂ e ₃ donne

${\displaystyle \mathbf {A} =\mathbf {a} i\,,\quad \mathbf {a} =-\mathbf {A} i.}$

Ceci est plus facile à utiliser car le produit n'est que le produit géométrique. Mais il est antisymétrique car (comme en deux dimensions) l'unité pseudoscalaire i est au carré de -1, donc un négatif est nécessaire dans l'un des produits.

Cette relation s'étend à des opérations telles que le produit vectoriel à valeur croisée et le produit extérieur à valeur bivecteur, car lorsqu'elles sont écrites en tant que déterminants, elles sont calculées de la même manière :

${\displaystyle \mathbf {a} \times \mathbf {b} ={\begin{vmatrix}\mathbf {e} _{1}&\mathbf {e} _{2}&\mathbf {e} _{3 }\\a_{1}&a_{2}&a_{3}\\b_{1}&b_{2}&b_{3}\end{vmatrix}}\,,\quad \mathbf {a} \wedge \mathbf { b} ={\begin{vmatrix}\mathbf {e} _{23}&\mathbf {e} _{31}&\mathbf {e} _{12}\\a_{1}&a_{2}&a_{ 3}\\b_{1}&b_{2}&b_{3}\end{vmatrix}}\ ,}$

sont donc liés par le dual de Hodge :

${\displaystyle {*(\mathbf {a} \wedge \mathbf {b} )}=\mathbf {a\times b} \,,\quad {*(\mathbf {a\times b} )}=\mathbf {a} \coin \mathbf {b} .}$

Les bivecteurs présentent un certain nombre d'avantages par rapport aux vecteurs axiaux. Ils désambiguisent mieux les vecteurs axiaux et polaires, c'est-à-dire les quantités qu'ils représentent, de sorte qu'il est plus clair quelles opérations sont autorisées et quels sont leurs résultats. Par exemple, le produit interne d'un vecteur polaire et d'un vecteur axial résultant du produit vectoriel dans le triple produit devrait donner un pseudoscalaire , un résultat qui est plus évident si le calcul est défini comme le produit extérieur d'un vecteur et d'un bivecteur. Ils se généralisent à d'autres dimensions ; en particulier, les bivecteurs peuvent être utilisés pour décrire des quantités telles que le couple et le moment cinétique en deux ou trois dimensions. En outre, ils correspondent étroitement à l'intuition géométrique de plusieurs manières, comme on le verra dans la section suivante.

Interprétation géométrique

Comme le suggèrent leur nom et celui de l'algèbre, l'un des attraits des bivecteurs est qu'ils ont une interprétation géométrique naturelle. Cela peut être décrit dans n'importe quelle dimension, mais il est préférable de le faire dans trois où des parallèles peuvent être tracés avec des objets plus familiers, avant d'être appliqués à des dimensions plus élevées. En deux dimensions, l'interprétation géométrique est triviale, car l'espace est bidimensionnel et n'a donc qu'un seul plan, et tous les bivecteurs y sont associés ne différant que par un facteur d'échelle.

Tous les bivecteurs peuvent être interprétés comme des plans , ou plus précisément comme des segments plans orientés. En trois dimensions, il y a trois propriétés d'un bivecteur qui peuvent être interprétées géométriquement :

• La disposition du plan dans l'espace, précisément l' attitude du plan (ou alternativement la rotation , l'orientation géométrique ou le gradient du plan), est associée au rapport des composantes bivecteur. En particulier les trois bivecteurs de base, e ₂₃ , e ₃₁ et e ₁₂ , ou leurs multiples scalaires, sont associés respectivement au plan yz , au plan zx et au plan xy .
• L' amplitude du bivecteur est associée à l' aire du segment plan. La zone n'a pas de forme particulière, donc n'importe quelle forme peut être utilisée. Il peut même être représenté d'autres manières, comme par une mesure angulaire. Mais si les vecteurs sont interprétés comme des longueurs, le bivecteur est généralement interprété comme une zone avec les mêmes unités, comme suit.
• Comme la direction d'un vecteur, un plan associé à un bivecteur a une direction, une circulation ou un sens de rotation dans le plan, qui prend deux valeurs dans le sens des aiguilles d' une montre et dans le sens inverse des aiguilles d' une montre lorsqu'il est vu d'un point de vue non dans le plan. Ceci est associé à un changement de signe dans le bivecteur, c'est-à-dire que si la direction est inversée, le bivecteur est annulé. Alternativement, si deux bivecteurs ont la même attitude et la même amplitude mais des directions opposées, l'un est le négatif de l'autre.
• Si on l'imagine comme un parallélogramme, avec l'origine des vecteurs à 0, alors l'aire signée est le déterminant des coordonnées cartésiennes des vecteurs ( a _x b _y − b _x a _y ).

En trois dimensions, tous les bivecteurs peuvent être générés par le produit extérieur de deux vecteurs. Si le bivecteur B = a ∧ b alors la magnitude de B est

${\displaystyle \left|\mathbf {B} \right|=\left|\mathbf {a} \right|\left|\mathbf {b} \right|\sin {\theta },}$

où θ est l'angle entre les vecteurs. C'est l'aire du parallélogramme avec les arêtes a et b , comme le montre le diagramme. Une interprétation est que la zone est balayée par b lorsqu'elle se déplace le long de a . Le produit est antisymétrique extérieur, de sorte que l' inversion de l'ordre de un et b pour faire un mouvement le long de b résultats dans un bivecteur avec la direction opposée qui est le négatif de la première. Le plan du bivecteur a ∧ b contient à la fois a et b , ils sont donc tous deux parallèles au plan.

Les bivecteurs et les vecteurs axiaux sont liés par Hodge dual . Dans un espace vectoriel réel, le dual de Hodge relie un sous-espace à son complément orthogonal , donc si un bivecteur est représenté par un plan, le vecteur axial qui lui est associé est simplement la normale à la surface du plan . Le plan a deux normales, une de chaque côté, donnant les deux orientations possibles pour le plan et le bivecteur.

Cela concerne le produit croisé du produit extérieur . Il peut également être utilisé pour représenter des grandeurs physiques, comme le couple et le moment cinétique . En algèbre vectorielle, ils sont généralement représentés par des vecteurs perpendiculaires au plan de la force , de la quantité de mouvement linéaire ou du déplacement à partir desquels ils sont calculés. Mais si un bivecteur est utilisé à la place, le plan est le plan du bivecteur, c'est donc une façon plus naturelle de représenter les quantités et la façon dont elles agissent. Contrairement à la représentation vectorielle, elle se généralise également dans d'autres dimensions.

Le produit de deux bivecteurs a une interprétation géométrique. Pour les bivecteurs non nuls A et B, le produit peut être divisé en parties symétriques et antisymétriques comme suit :

${\displaystyle \mathbf {AB} =\mathbf {A} \cdot \mathbf {B} +\mathbf {A} \times \mathbf {B} .}$

Comme les vecteurs, ceux-ci ont des grandeurs | A ⋅ B | = | A | | B | cos θ et | A × B | = | A | | B | sin θ , où θ est l'angle entre les plans. En trois dimensions, c'est le même que l'angle entre les vecteurs normaux duaux aux plans, et il se généralise dans une certaine mesure dans les dimensions supérieures.

Les bivecteurs peuvent être additionnés en tant que zones. Compte tenu de deux bivecteurs de non nuls B et C en trois dimensions , il est toujours possible de trouver un vecteur qui est contenu dans les deux, un mot à dire, de sorte que les bivecteurs peuvent être écrits sous forme de produits extérieurs impliquant un :

${\displaystyle {\begin{aligned}\mathbf {B} &=\mathbf {a} \wedge \mathbf {b} \\\mathbf {C} &=\mathbf {a} \wedge \mathbf {c} \ fin{aligné}}}$

Ceci peut être interprété géométriquement comme le montre le schéma : les deux aires s'additionnent pour en donner une troisième, les trois aires formant les faces d'un prisme avec a , b , c et b + c comme arêtes. Cela correspond aux deux façons de calculer la surface en utilisant la distributivité du produit extérieur :

${\displaystyle {\begin{aligné}\mathbf {B} +\mathbf {C} &=\mathbf {a} \wedge \mathbf {b} +\mathbf {a} \wedge \mathbf {c} \\& =\mathbf {a} \wedge (\mathbf {b} +\mathbf {c} ).\end{aligned}}}$

Cela ne fonctionne qu'en trois dimensions car c'est la seule dimension où un vecteur parallèle aux deux bivecteurs doit exister. Dans des dimensions supérieures, les bivecteurs ne sont généralement pas associés à un seul plan, ou s'ils le sont (des bivecteurs simples), deux bivecteurs peuvent n'avoir aucun vecteur en commun, et donc s'additionner à un bivecteur non simple.

Quatre dimensions

En quatre dimensions les éléments de base pour l'espace ⋀ ² R ⁴ des bivecteurs sont ( e ₁₂ , e ₁₃ , e ₁₄ , e ₂₃ , e ₂₄ , e ₃₄ ), donc un bivecteur général est de la forme

${\displaystyle \mathbf {A} =a_{12}\mathbf {e} _{12}+a_{13}\mathbf {e} _{13}+a_{14}\mathbf {e} _{14} +a_{23}\mathbf {e} _{23}+a_{24}\mathbf {e} _{24}+a_{34}\mathbf {e} _{34}.}$

Orthogonalité

En quatre dimensions le dual de Hodge d'un bivecteur est un bivecteur, et l'espace ⋀ ² R ⁴ est dual à lui-même. Les vecteurs normaux ne sont pas uniques, à la place chaque plan est orthogonal à tous les vecteurs dans son espace dual de Hodge. Cela peut être utilisé pour diviser les bivecteurs en deux « moitiés », de la manière suivante. On a trois paires de bivecteurs orthogonaux : ( e ₁₂ , e ₃₄ ), ( e ₁₃ , e ₂₄ ) et ( e ₁₄ , e ₂₃ ). Il existe quatre manières distinctes de choisir un bivecteur dans chacune des deux premières paires, et une fois que ces deux premières sont sélectionnées, leur somme donne le troisième bivecteur de l'autre paire. Par exemple, ( e ₁₂ , e ₁₃ , e ₁₄ ) et ( e ₂₃ , e ₂₄ , e ₃₄ ).

Bivecteurs simples en 4D

En quatre dimensions, les bivecteurs sont générés par le produit extérieur des vecteurs dans R ⁴ , mais avec une différence importante par rapport à R ³ et R ² . En quatre dimensions, tous les bivecteurs ne sont pas simples. Il existe des bivecteurs tels que e ₁₂ + e ₃₄ qui ne peuvent pas être générés par le produit extérieur de deux vecteurs. Cela signifie également qu'ils n'ont pas de réel, c'est-à-dire scalaire, carré. Dans ce cas

${\displaystyle (\mathbf {e} _{12}+\mathbf {e} _{34})^{2}=\mathbf {e} _{12}\mathbf {e} _{12}+\mathbf {e} _{12}\mathbf {e} _{34}+\mathbf {e} _{34}\mathbf {e} _{12}+\mathbf {e} _{34}\mathbf {e} _{34}=-2+2\mathbf {e} _{1234}.}$

L'élément e ₁₂₃₄ est le pseudoscalaire dans Cl ₄ , distinct du scalaire, donc le carré est non scalaire.

Tous les bivecteurs en quatre dimensions peuvent être générés en utilisant au plus deux produits extérieurs et quatre vecteurs. Le bivecteur ci-dessus peut être écrit comme

${\displaystyle \mathbf {e} _{12}+\mathbf {e} _{34}=\mathbf {e} _{1}\wedge \mathbf {e} _{2}+\mathbf {e} _ {3}\coin \mathbf {e} _{4}.}$

De même, chaque bivecteur peut être écrit comme la somme de deux bivecteurs simples. Il est utile de choisir pour cela deux bivecteurs orthogonaux, ce qui est toujours possible. De plus, pour un bivecteur générique, le choix des bivecteurs simples est unique, c'est-à-dire qu'il n'y a qu'une seule façon de décomposer en bivecteurs orthogonaux ; la seule exception est lorsque les deux bivecteurs orthogonaux ont des grandeurs égales (comme dans l'exemple ci-dessus) : dans ce cas, la décomposition n'est pas unique. La décomposition est toujours unique dans le cas des bivecteurs simples, avec en prime qu'une des parties orthogonales est nulle.

Rotations en R ⁴

Comme en trois dimensions, les bivecteurs en quatre dimensions génèrent des rotations à travers la carte exponentielle, et toutes les rotations peuvent être générées de cette façon. Comme en trois dimensions si B est un bivecteur alors le rotor R est e ^{B /2} et les rotations sont générées de la même manière :

${\displaystyle v'=RvR^{-1}.\,}$

Les rotations générées sont cependant plus complexes. Ils peuvent être classés comme suit :

les rotations simples sont celles qui fixent un plan dans 4D, et tournent d'un angle "autour" de ce plan.

les doubles rotations n'ont qu'un seul point fixe, l'origine, et tournent selon deux angles autour de deux plans orthogonaux. En général, les angles sont différents et les plans sont spécifiés de manière unique

Les rotations isocliniques sont des rotations doubles où les angles de rotation sont égaux. Dans ce cas, les plans autour desquels s'effectue la rotation ne sont pas uniques.

Ceux-ci sont générés par des bivecteurs de manière simple. Les rotations simples sont générées par des bivecteurs simples, avec le plan fixe duel ou orthogonal au plan du bivecteur. On peut dire que la rotation a lieu autour de ce plan, dans le plan du bivecteur. Tous les autres bivecteurs génèrent des rotations doubles, les deux angles de rotation étant égaux aux magnitudes des deux bivecteurs simples dont le bivecteur non simple est composé. Les rotations isocliniques surviennent lorsque ces grandeurs sont égales, auquel cas la décomposition en deux bivecteurs simples n'est pas unique.

Les bivecteurs en général ne commutent pas, mais une exception sont les bivecteurs orthogonaux et leurs exposants. Donc, si le bivecteur B = B ₁ + B ₂ , où B ₁ et B ₂ sont des bivecteurs simples orthogonaux, est utilisé pour générer une rotation, il se décompose en deux rotations simples qui commutent comme suit :

${\displaystyle R=e^{\frac {\mathbf {B} _{1}+\mathbf {B} _{2}}{2}}=e^{\frac {\mathbf {B} _{1 }}{2}}e^{\frac {\mathbf {B} _{2}}{2}}=e^{\frac {\mathbf {B} _{2}}{2}}e^{ \frac {\mathbf {B} _{1}}{2}}}$

Il est toujours possible de le faire car tous les bivecteurs peuvent être exprimés comme des sommes de bivecteurs orthogonaux.

Rotations espace-temps

L'espace-temps est un modèle mathématique de notre univers utilisé en relativité restreinte. Il se compose de trois dimensions spatiales et d'une dimension temporelle combinées en un seul espace à quatre dimensions. Elle est naturellement décrite à l'aide d'algèbre géométrique et de bivecteurs, la métrique euclidienne étant remplacée par une métrique de Minkowski . Cette algèbre est identique à celle de l'espace euclidien, sauf que la signature est modifiée, donc

${\displaystyle {\mathbf {e} _{i}}^{2}={\begin{cases}1,&i=1,2,3\\-1,&i=4\end{cases}}}$

(Notez que l'ordre et les indices ci-dessus ne sont pas universels - ici e ₄ est la dimension temporelle). L'algèbre géométrique est Cl _3,1 ( R ), et le sous-espace des bivecteurs est ⋀ ² R ^3,1 .

Les bivecteurs simples sont de deux types. Les bivecteurs simples e ₂₃ , e ₃₁ et e ₁₂ ont des carrés négatifs et couvrent les bivecteurs du sous-espace tridimensionnel correspondant à l'espace euclidien, R ³ . Ces bivecteurs génèrent des rotations ordinaires dans R ³ .

Les bivecteurs simples e ₁₄ , e ₂₄ et e ₃₄ ont des carrés positifs et couvrent comme plans une dimension d'espace et la dimension de temps. Celles-ci génèrent également des rotations via la carte exponentielle, mais au lieu de fonctions trigonométriques, des fonctions hyperboliques sont nécessaires, ce qui génère un rotor comme suit :

${\displaystyle e^{\frac {{\boldsymbol {\Omega }}\theta }{2}}=\cosh \left({\frac {\theta }{2}}\right)+{\boldsymbol {\ Omega }}\sinh \left({\frac {\theta }{2}}\right),}$

où Ω est le bivecteur ( e ₁₄ , etc.), identifié par la métrique d'une transformation linéaire antisymétrique de R ^3,1 . Il s'agit des boosts de Lorentz , exprimés de manière particulièrement compacte, utilisant le même type d'algèbre que dans R ³ et R ⁴ .

En général, toutes les rotations de l'espace-temps sont générées à partir de bivecteurs via la carte exponentielle, c'est-à-dire qu'un rotor général généré par le bivecteur A est de la forme

${\displaystyle R=e^{\frac {\mathbf {A} }{2}}.}$

L'ensemble de toutes les rotations dans l'espace-temps forme le groupe de Lorentz , et à partir d'eux la plupart des conséquences de la relativité restreinte peuvent être déduites. Plus généralement, cela montre comment les transformations dans l'espace euclidien et l'espace-temps peuvent toutes être décrites en utilisant le même type d'algèbre.

les équations de Maxwell

(Remarque : dans cette section, les 3-vecteurs traditionnels sont indiqués par des lignes sur les symboles et le vecteur espace-temps et les bivecteurs par des symboles en gras, avec les vecteurs J et A exceptionnellement en majuscule)

Les équations de Maxwell sont utilisées en physique pour décrire la relation entre les champs électriques et magnétiques . Normalement données sous forme de quatre équations différentielles, elles ont une forme particulièrement compacte lorsque les champs sont exprimés sous la forme d'un bivecteur espace-temps à partir de ⋀ ² R ^3,1 . Si les champs électrique et magnétique dans R ³ sont E et B alors le bivecteur électromagnétique est

${\displaystyle \mathbf {F} ={\frac {1}{c}}{\overline {E}}\mathbf {e} _{4}+{\overline {B}}\mathbf {e} _{ 123},}$

où e ₄ est à nouveau le vecteur de base pour la dimension temporelle et c est la vitesse de la lumière . Le produit B e ₁₂₃ rendements du bivecteur qui est Hodge double de B en trois dimensions, comme discuté ci - dessus , tandis que E e ₄ en tant que produit de vecteurs orthogonaux est également évaluée bivecteur. Dans l'ensemble, c'est le tenseur électromagnétique exprimé de manière plus compacte sous forme de bivecteur, et est utilisé comme suit. Tout d'abord, il est lié au 4-courant J , une quantité vectorielle donnée par

${\displaystyle \mathbf {J} ={\overline {j}}+c\rho \mathbf {e} _{4},}$

où j est la densité de courant et ρ est la densité de charge . Ils sont liés par un opérateur différentiel ∂, qui est

${\displaystyle \partial =\nabla -\mathbf {e} _{4}{\frac {1}{c}}{\frac {\partial }{\partial t}}.}$

L'opérateur ∇ est un opérateur différentiel en algèbre géométrique, agissant sur les dimensions de l'espace et donné par ∇ M = ∇⋅ M + ∇∧ M . Lorsqu'il est appliqué aux vecteurs, ∇⋅ M est la divergence et ∇∧ M est la boucle, mais avec un résultat bivecteur plutôt que vectoriel, c'est-à-dire duel en trois dimensions à la boucle. Pour la quantité générale M, ils jouent le rôle d'opérateurs différentiels d'abaissement et d'élévation du grade. En particulier, si M est un scalaire, alors cet opérateur n'est que le gradient , et il peut être considéré comme un opérateur algébrique géométrique del .

Ensemble, ils peuvent être utilisés pour donner une forme particulièrement compacte aux équations de Maxwell avec des sources :

${\displaystyle \partial \mathbf {F} =\mathbf {J} .}$

Cette équation, lorsqu'elle est décomposée selon l'algèbre géométrique, en utilisant des produits géométriques qui ont à la fois des effets d'élévation et d'abaissement des notes, est équivalente aux quatre équations de Maxwell. Il est également lié au quatre-potentiel électromagnétique , un vecteur A donné par

${\displaystyle \mathbf {A} ={\overline {A}}+{\frac {1}{c}}V\mathbf {e} _{4},}$

où A est le potentiel magnétique vectoriel et V est le potentiel électrique. Il est lié au bivecteur électromagnétique comme suit

${\displaystyle \partial \mathbf {A} =-\mathbf {F} ,}$

en utilisant le même opérateur différentiel ∂.

Dimensions supérieures

Comme cela a été suggéré dans les sections précédentes, une grande partie de l'algèbre géométrique se généralise bien dans des dimensions supérieures. L'algèbre géométrique de l'espace réel R ⁿ est Cl _n ( R ), et le sous-espace des bivecteurs est ⋀ ² R ⁿ .

Le nombre de bivecteurs simples nécessaires pour former un bivecteur général augmente avec la dimension, donc pour n impair c'est ( n − 1) / 2 , pour n pair c'est n / 2 . Ainsi, pour quatre et cinq dimensions, seuls deux bivecteurs simples sont nécessaires, mais trois sont nécessaires pour six et sept dimensions. Par exemple, en six dimensions à base standard ( e ₁ , e ₂ , e ₃ , e ₄ , e ₅ , e ₆ ) le bivecteur

${\displaystyle \mathbf {e} _{12}+\mathbf {e} _{34}+\mathbf {e} _{56}}$

est la somme de trois bivecteurs simples mais pas moins. Comme en quatre dimensions il est toujours possible de trouver des bivecteurs simples orthogonaux pour cette somme.

Rotations dans des dimensions supérieures

Comme dans les trois et quatre dimensions, les rotors sont générés par la carte exponentielle, donc

${\displaystyle e^{\frac {\mathbf {B} }{2}}}$

est le rotor engendré par le bivecteur B . Les rotations simples, qui ont lieu dans un plan de rotation autour d'une lame fixe de dimension ( n − 2) sont générées par des bivecteurs simples, tandis que d'autres bivecteurs génèrent des rotations plus complexes qui peuvent être décrites en termes de bivecteurs simples dont ils sont les sommes, chacun lié à un plan de rotation. Tous les bivecteurs peuvent être exprimés comme la somme de bivecteurs simples orthogonaux et commutatifs, de sorte que les rotations peuvent toujours être décomposées en un ensemble de rotations commutatives autour des plans associés à ces bivecteurs. Le groupe des rotors en n dimensions est le groupe de spin , Spin( n ).

Une caractéristique notable, liée au nombre de bivecteurs simples et donc de plans de rotation, est que dans les dimensions impaires, chaque rotation a un axe fixe - il est trompeur de l'appeler un axe de rotation car dans les dimensions supérieures, les rotations ont lieu dans plusieurs plans orthogonaux. à cela. Ceci est lié aux bivecteurs, car les bivecteurs de dimensions impaires se décomposent en le même nombre de bivecteurs que la dimension paire ci-dessous, ils ont donc le même nombre de plans, mais une dimension supplémentaire. Comme chaque plan génère des rotations dans deux dimensions dans des dimensions impaires, il doit y avoir une dimension, c'est-à-dire un axe, qui n'est pas en rotation.

Les bivecteurs sont également liés à la matrice de rotation en n dimensions. Comme en trois dimensions l' équation caractéristique de la matrice peut être résolue pour trouver les valeurs propres . Dans les dimensions impaires, cela a une racine réelle, avec le vecteur propre l'axe fixe, et dans les dimensions paires, il n'a pas de racines réelles, donc toutes ou toutes sauf une des racines sont des paires conjuguées complexes. Chaque paire est associée à une composante simple du bivecteur associé à la rotation. En particulier, le log de chaque paire est de ± la magnitude, tandis que les vecteurs propres générés à partir des racines sont parallèles et peuvent donc être utilisés pour générer le bivecteur. En général, les valeurs propres et les bivecteurs sont uniques, et l'ensemble des valeurs propres donne la décomposition complète en bivecteurs simples ; si les racines sont répétées alors la décomposition du bivecteur en bivecteurs simples n'est pas unique.

Géométrie projective

L'algèbre géométrique peut être appliquée à la géométrie projective d'une manière simple. L'algèbre géométrique utilisée est Cl _n ( R ), n 3 , l'algèbre de l'espace vectoriel réel R ⁿ . Ceci est utilisé pour décrire des objets dans l' espace projectif réel RP ^{n -1} . Les vecteurs non nuls dans Cl _n ( R ) ou R ⁿ sont associés à des points de l'espace projectif, de sorte que les vecteurs qui ne diffèrent que par un facteur d'échelle, donc leur produit extérieur est nul, sont mappés au même point. Les bivecteurs simples non nuls dans ² R ⁿ représentent des droites dans RP ^{n -1} , les bivecteurs ne différant que par un facteur d'échelle (positif ou négatif) représentant la même droite.

Une description de la géométrie projective peut être construite dans l'algèbre géométrique en utilisant des opérations de base. Par exemple, étant donné deux points distincts de RP ^{n -1} représentés par les vecteurs a et b la ligne les contenant est donnée par a ∧ b (ou b ∧ a ). Deux lignes se croisent en un point si A ∧ B = 0 pour leurs bivecteurs A et B . Ce point est donné par le vecteur

${\displaystyle \mathbf {p} =\mathbf {A} \lor \mathbf {B} =(\mathbf {A} \times \mathbf {B} )J^{-1}.}$

L'opération « ∨ » est la rencontre, qui peut être défini comme ci - dessus en termes de la jointure, J = A ∧ B pour les non-zéro A ∧ B . En utilisant ces opérations, la géométrie projective peut être formulée en termes d'algèbre géométrique. Par exemple, étant donné un troisième bivecteur (non nul) C le point p se trouve sur la ligne donnée par C si et seulement si

${\displaystyle \mathbf {p} \land \mathbf {C} =0.}$

Donc la condition pour que les droites données par A , B et C soient colinéaires est

${\displaystyle (\mathbf {A} \lor \mathbf {B} )\land \mathbf {C} =0,}$

qui dans Cl ₃ ( R ) et RP ^{2 se} simplifie en

${\displaystyle \langle \mathbf {ABC} \rangle =0,}$

où les crochets angulaires désignent la partie scalaire du produit géométrique. De la même manière, toutes les opérations spatiales projectives peuvent être écrites en termes d'algèbre géométrique, avec des bivecteurs représentant des lignes générales dans l'espace projectif, de sorte que toute la géométrie peut être développée en utilisant l'algèbre géométrique.

Tenseurs et matrices

Comme indiqué ci - dessus, un bivecteur peut être écrit sous la forme d'une matrice antisymétrique qui, à travers la carte exponentielle, génère une matrice de rotation qui décrit la même rotation que le rotor, également générée par la carte exponentielle mais appliquée au vecteur. Mais il est également utilisé avec d'autres bivecteurs tels que le tenseur de vitesse angulaire et le tenseur électromagnétique , respectivement une matrice ou un tenseur antisymétrique 3×3 et 4×4.

Les bivecteurs réels dans ⋀ ² R ⁿ sont des matrices isomorphes à n × n antisymétriques, ou alternativement à des tenseurs antisymétriques de degré 2 sur R ⁿ . Alors que les bivecteurs sont isomorphes aux vecteurs (via le dual) en trois dimensions, ils peuvent être représentés par des matrices antisymétriques dans n'importe quelle dimension. Ceci est utile pour relier les bivecteurs à des problèmes décrits par des matrices, afin qu'ils puissent être reformulés en termes de bivecteurs, étant donné une interprétation géométrique, puis souvent résolus plus facilement ou liés géométriquement à d'autres problèmes bivecteurs.

Plus généralement toute algèbre géométrique réelle est isomorphe à une algèbre matricielle . Ceux-ci contiennent des bivecteurs en tant que sous-espace, bien que souvent d'une manière qui n'est pas particulièrement utile. Ces matrices sont principalement intéressantes pour classer les algèbres de Clifford.

Voir également

• Multivecteur
• Algèbre multilinéaire

Remarques

Références générales

• Léo Dorst ; Daniel Fontijne ; Stephen Mann (2009). "§ 2.3.3 Visualisation des bivecteurs" . Algèbre géométrique pour l'informatique: une approche orientée objet de la géométrie (2e éd.). Morgan Kaufmann. p. 31 sqq . ISBN 978-0-12-374942-0.
• Whitney, Hassler (1957). Théorie de l'intégration géométrique . Princeton : Princeton University Press . ISBN 978-0-486-44583-0.

• Lounesto, Pertti (2001). Algèbres et spineurs de Clifford . Cambridge : Cambridge University Press . ISBN 978-0-521-00551-7.

• Chris Doran & Anthony Lasenby (2003). "§ 1.6 Le produit extérieur" . Algèbre géométrique pour les physiciens . Cambridge : Cambridge University Press . p. 11 et suiv . ISBN 978-0-521-71595-9.