Lois de la forme -Laws of Form
Laws of Form (ci-après LoF ) est un livre de G. Spencer-Brown , publié en 1969, qui chevauche la frontière entre les mathématiques et la philosophie . LoF décrit trois systèmes logiques distincts:
- L'« arithmétique primaire » (décrite au chapitre 4 de LoF ), dont les modèles incluent l'arithmétique booléenne ;
- L'« algèbre primaire » (chapitre 6 de LoF ), dont les modèles incluent l' algèbre booléenne à deux éléments (ci-après abrégée 2 ), la logique booléenne et le calcul propositionnel classique ;
- « Equations du second degré » (chapitre 11), dont les interprétations incluent les automates finis et l' arithmétique récursive restreinte d' Alonzo Church (RRA).
« Algèbre des limites » est le terme de Meguire (2011) pour l'union de l'algèbre primaire et de l'arithmétique primaire. Les lois de la forme se réfèrent parfois vaguement à "l'algèbre primaire" ainsi qu'à LoF .
Le livre
La préface indique que l'œuvre a été explorée pour la première fois en 1959, et Spencer Brown cite Bertrand Russell comme soutenant son entreprise. Il remercie également JCP Miller de l' University College de Londres pour avoir aidé à la relecture et offert d'autres conseils. En 1963, Spencer Brown a été invité par Harry Frost , maître de conférences en sciences physiques au département d'études extra-murales de l' Université de Londres pour donner un cours sur les mathématiques de la logique.
LoF a émergé des travaux d'ingénierie électronique que son auteur a effectués vers 1960, et des conférences ultérieures sur la logique mathématique qu'il a données sous les auspices du programme d'extension de l' Université de Londres . LoF est apparu dans plusieurs éditions. La deuxième série d'éditions paraît en 1972 avec la « Préface à la première édition américaine » qui met l'accent sur l'utilisation de paradoxes autoréférentiels. la plus récente étant une traduction allemande de 1997, et n'a jamais été épuisée.
Les mathématiques ne remplissent qu'environ 55pp et sont plutôt élémentaires. Mais « LoF prose mystique et déclamatoire s, et son amour du paradoxe , en font un difficile lire pour tous. Spencer-Brown a été influencé par Wittgenstein et RD Laing . LoF fait également écho à un certain nombre de thèmes des écrits de Charles Sanders Peirce , Bertrand Russell et Alfred North Whitehead .
Le livre entier est écrit de manière opérationnelle, donnant des instructions au lecteur au lieu de lui dire ce qui « est ». Conformément à l'intérêt de G. Spencer-Brown pour les paradoxes, la seule phrase qui fait une déclaration que quelque chose est, est la déclaration, qui dit qu'aucune de ces déclarations n'est utilisée dans ce livre. À l'exception de cette seule phrase, le livre peut être considéré comme un exemple d' E-Prime .
accueil
Ostensiblement un ouvrage de mathématiques formelles et de philosophie, LoF est devenu en quelque sorte un classique culte : il a été salué par Heinz von Foerster lorsqu'il l'a examiné pour le Whole Earth Catalog . Ceux qui sont d'accord indiquent que LoF incarne une « mathématiques de la conscience » énigmatique , son symbolisme algébrique capturant une (peut-être même « la ») racine implicite de la cognition : la capacité de « distinguer ». LoF soutient que l'algèbre primaire révèle des liens frappants entre la logique , l'algèbre booléenne et l'arithmétique, et la philosophie du langage et de l' esprit .
Banaschewski (1977) soutient que l'algèbre primaire n'est rien d'autre qu'une nouvelle notation pour l'algèbre booléenne. En effet, l' algèbre booléenne à deux éléments 2 peut être considérée comme l'interprétation voulue de l'algèbre primaire. Pourtant la notation de l'algèbre primaire :
- Exploite pleinement la dualité caractérisant non seulement les algèbres booléennes mais tous les treillis ;
- Met en évidence comment des déclarations syntaxiquement distinctes en logique et 2 peuvent avoir une sémantique identique ;
- Simplifie considérablement les calculs d'algèbre booléenne et les preuves en logique propositionnelle et syllogistique .
De plus, la syntaxe de l'algèbre primaire peut être étendue à des systèmes formels autres que 2 et la logique propositionnelle, résultant en des mathématiques de frontière (voir § Travaux connexes ci-dessous).
LoF a influencé, entre autres, Heinz von Foerster , Louis Kauffman , Niklas Luhmann , Humberto Maturana , Francisco Varela et William Bricken . Certains de ces auteurs ont modifié l'algèbre primaire de diverses manières intéressantes.
LoF a affirmé que certaines conjectures mathématiques bien connues de très longue date, telles que le théorème des quatre couleurs , le dernier théorème de Fermat et la conjecture de Goldbach , sont prouvables en utilisant des extensions de l'algèbre primaire. Spencer-Brown a finalement fait circuler une prétendue preuve du théorème des quatre couleurs, mais elle a suscité le scepticisme.
Le formulaire (Chapitre 1)
Le symbole:
Aussi appelée « marque » ou « croix », est la caractéristique essentielle des lois de la forme. À la manière inimitable et énigmatique de Spencer-Brown, la Marque symbolise la racine de la cognition , c'est-à-dire que la Marque dualiste indique la capacité de différencier un « ceci » de « tout le reste sauf ceci ».
Dans LoF , une croix dénote le dessin d'une « distinction » et peut être considérée comme signifiant ce qui suit, à la fois :
- Action de tracer une frontière autour de quelque chose, le séparant ainsi de tout le reste ;
- Ce qui se distingue de tout en traçant la frontière ;
- Passage d'un côté à l'autre de la frontière.
Les trois manières impliquent une action de la part de l'entité cognitive (par exemple, la personne) faisant la distinction. Comme le dit LoF :
"La première commande :
- Faire une distinction
peut bien s'exprimer ainsi :
- Qu'il y ait une distinction,
- Trouver une distinction,
- Voir une distinction,
- Décrire une distinction,
- Définir une distinction,
Ou alors:
- Qu'une distinction soit faite". ( LoF , Notes au chapitre 2)
Le contrepoint à l'état Marqué est l'état Non-marqué, qui n'est tout simplement rien, le vide, ou l'infini inexprimable représenté par un espace blanc. C'est simplement l'absence d'une Croix. Aucune distinction n'a été faite et rien n'a été franchi. L'état Marqué et le vide sont les deux valeurs primitives des Lois de la Forme.
La Croix peut être considérée comme désignant la distinction entre deux états, l'un "considéré comme un symbole" et l'autre pas ainsi considéré. De ce fait naît une curieuse résonance avec certaines théories de la conscience et du langage . Paradoxalement, la Forme est à la fois Observatrice et Observée, et est aussi l'acte créateur de faire une observation. LoF (à l'exclusion de la matière arrière) se termine par les mots :
... la première distinction, la Marque et l'observateur ne sont pas seulement interchangeables, mais, dans la forme, identiques.
CS Peirce est venu à une idée connexe dans les années 1890; voir § Travaux connexes .
L'arithmétique primaire (Chapitre 4)
La syntaxe de l'arithmétique primaire est la suivante. Il n'y a que deux expressions atomiques :
Il existe deux règles inductives :
- Une croix
 peut être écrite sur n'importe quelle expression;
peut être écrite sur n'importe quelle expression; - Deux expressions peuvent être concaténées .
La sémantique de l'arithmétique primaire n'est peut-être que la seule définition explicite de LoF : "La distinction est la continence parfaite".
Que l'"état non marqué" soit synonyme de vide. Soit une croix vide dénoter "l'état marqué". Traverser, c'est passer d'une valeur, l'état non marqué ou marqué, à l'autre. Nous pouvons maintenant énoncer les axiomes « arithmétiques » A1 et A2, qui fondent l'arithmétique primaire (et donc toutes les lois de la forme) :
"A1. La loi de l'appel". Appeler deux fois depuis un état est indiscernable d'appeler une fois. Faire une distinction deux fois a le même effet que la faire une fois. Par exemple, dire « Que la lumière soit » puis dire à nouveau « Que la lumière soit » revient à le dire une fois. Officiellement:
"A2. La loi de la traversée". Après le passage de l'état non marqué à l'état marqué, un nouveau croisement ("recroisement") à partir de l'état marqué ramène l'un à l'état non marqué. Le recroisement annule donc le croisement. Officiellement:
Dans A1 et A2, l'expression à droite de '=' a moins de symboles que l'expression à gauche de '='. Cela suggère que chaque expression arithmétique primaire peut, par application répétée de A1 et A2, être simplifiée en l'un des deux états suivants : l'état marqué ou non marqué. C'est bien le cas, et le résultat est la "simplification" de l'expression. Les deux métathéorèmes fondamentaux de l'arithmétique primaire déclarent que :
- Chaque expression finie a une simplification unique. (T3 en LoF );
- Partant d'un état initial marqué ou non marqué, « compliquer » une expression par un nombre fini d'applications répétées de A1 et A2 ne peut donner une expression dont la simplification diffère de l'état initial. (T4 en LoF ).
Ainsi, la relation d' équivalence logique divise toutes les expressions arithmétiques primaires en deux classes d'équivalence : celles qui simplifient jusqu'à la croix et celles qui simplifient jusqu'au vide.
A1 et A2 ont des analogues lâches dans les propriétés des circuits électriques en série et en parallèle, et dans d'autres manières de schématiser les processus, y compris l'organigramme. A1 correspond à une connexion en parallèle et A2 à une connexion en série, étant entendu que faire une distinction correspond à changer la façon dont deux points d'un circuit sont connectés, et pas simplement à ajouter du câblage.
L'arithmétique primaire est analogue aux langages formels suivants issus des mathématiques et de l' informatique :
- Un langage de Dyck d'ordre 1 avec un alphabet nul ;
- Le langage sans contexte le plus simple de la hiérarchie de Chomsky ;
- Un système de réécriture qui est fortement normalisant et confluentes .
L'expression « calcul des indications » dans LoF est un synonyme de « arithmétique primaire ».
La notion de canon
Un concept propre à LoF est celui de « canon ». Bien que LoF ne définisse pas le canon, les deux extraits suivants des Notes au chpt. 2 sont aptes :
Les structures de commandement les plus importantes sont parfois appelées canons . Ce sont les manières dont les injonctions directrices semblent se grouper en constellations, et ne sont donc en aucun cas indépendantes les unes des autres. Un canon porte la distinction d'être en dehors (c'est-à-dire de décrire) le système en construction, mais une commande de construire (par exemple, « faites une distinction »), même si elle peut être d'une importance centrale, n'est pas un canon. Un canon est un ordre, ou un ensemble d'ordres, pour permettre ou permettre, mais pas pour construire ou créer.
... la principale forme de communication mathématique n'est pas la description mais l'injonction... La musique est une forme d'art similaire, le compositeur n'essaie même pas de décrire l'ensemble de sons qu'il a en tête, encore moins l'ensemble des sentiments occasionnés à travers eux , mais écrit un ensemble de commandes qui, si elles sont obéies par l'interprète, peuvent aboutir à une reproduction, pour l'auditeur, de l'expérience originale du compositeur.
Ces extraits se rapportent à la distinction en métalogique entre le langage objet , le langage formel du système logique en discussion, et le métalangage , un langage (souvent un langage naturel) distinct du langage objet, utilisé pour exposer et discuter le langage objet. La première citation semble affirmer que les canons font partie du métalangage. La deuxième citation semble affirmer que les déclarations dans le langage objet sont essentiellement des commandes adressées au lecteur par l'auteur. Ni l'une ni l'autre de ces affirmations ne tient dans la métalogique standard.
L'algèbre primaire (Chapitre 6)
Syntaxe
Étant donné toute expression arithmétique primaire valide, insérez dans un ou plusieurs emplacements un nombre quelconque de lettres latines portant des indices numériques facultatifs ; le résultat est une formule d' algèbre primaire . Les lettres ainsi employées en mathématiques et en logique sont appelées variables . Une variable d'algèbre primaire indique un emplacement où l'on peut écrire la valeur primitive ![]() ou son complément
ou son complément ![]() . Plusieurs instances de la même variable désignent plusieurs emplacements de la même valeur primitive.
. Plusieurs instances de la même variable désignent plusieurs emplacements de la même valeur primitive.
Règles régissant l'équivalence logique
Le signe '=' peut lier deux expressions logiquement équivalentes ; le résultat est une équation . Par « logiquement équivalent », on entend que les deux expressions ont la même simplification. L'équivalence logique est une relation d'équivalence sur l'ensemble des formules algébriques primaires, régie par les règles R1 et R2. Soient "C" et "D" des formules contenant chacune au moins une instance de la sous-formule A :
- R1 , Substitution d'égaux . Remplacez une ou plusieurs instances de A dans C par B , ce qui donne E . Si A = B , alors C = E .
- R2 , Remplacement uniforme . Remplacez toutes les instances de A dans C et D par B . C devient E et D devient F . Si C = D , alors E = F . Notez que A = B n'est pas requis.
R2 est utilisé très fréquemment dans les démonstrations d' algèbre primaire (voir ci-dessous), presque toujours en silence. Ces règles sont couramment invoquées en logique et dans la plupart des mathématiques, presque toujours inconsciemment.
L' algèbre primaire est constituée d' équations , c'est-à-dire de paires de formules liées par un infixe '='. R1 et R2 permettent de transformer une équation en une autre. Par conséquent, l' algèbre primaire est un système formel équationnel , comme les nombreuses structures algébriques , y compris l'algèbre booléenne , qui sont des variétés . La logique équationnelle était courante avant les Principia Mathematica (par exemple, Peirce, 1,2,3 Johnson 1892), et a des défenseurs actuels (Gries et Schneider 1993).
La logique mathématique conventionnelle consiste en des formules tautologiques , signalées par un tourniquet préfixé . Pour indiquer que la formule algébrique primaire A est une tautologie , écrivez simplement " A = ![]() ". Si l'on remplace '=' dans R1 et R2 par le biconditionnel , les règles résultantes sont valables en logique conventionnelle. Cependant, la logique conventionnelle repose principalement sur la règle modus ponens ; ainsi la logique conventionnelle est ponctuelle . La dichotomie équationnelle-ponentielle distille une grande partie de ce qui distingue la logique mathématique du reste des mathématiques.
". Si l'on remplace '=' dans R1 et R2 par le biconditionnel , les règles résultantes sont valables en logique conventionnelle. Cependant, la logique conventionnelle repose principalement sur la règle modus ponens ; ainsi la logique conventionnelle est ponctuelle . La dichotomie équationnelle-ponentielle distille une grande partie de ce qui distingue la logique mathématique du reste des mathématiques.
Initiales
Une initiale est une équation algébrique primaire vérifiable par une procédure de décision et en tant que telle n'est pas un axiome . LoF pose les initiales :
|
|
= . |
L'absence de quoi que ce soit à droite du "=" ci-dessus, est délibérée.
|
|
C | = |
|
. |
J2 est la loi distributive familière de la logique phrastique et de l'algèbre booléenne .
Un autre ensemble d'initiales, plus convivial pour les calculs, est :
|
|
UNE | = | UNE. |
|
|
= |
|
. |
|
UNE |
|
= | UNE |
|
. |
C'est grâce à C2 que l' algèbre primaire est un treillis . En vertu de J1a , c'est un réseau complémenté dont la borne supérieure est ![]() . Par J0 ,
. Par J0 , ![]() est la borne inférieure et l' élément d'identité correspondants . J0 est également une version algébrique de A2 et précise le sens des
est la borne inférieure et l' élément d'identité correspondants . J0 est également une version algébrique de A2 et précise le sens des ![]() alias avec la page blanche.
alias avec la page blanche.
T13 dans LoF généralise C2 comme suit. Toute formule d' algèbre primaire (ou logique phrastique) B peut être considérée comme un arbre ordonné avec des branches . Puis:
T13 : Une sous-formule A peut être copiée à volonté dans n'importe quelle profondeur de B supérieure à celle de A , tant que A et sa copie sont dans la même branche de B . De plus, étant donné plusieurs instances de A dans la même branche de B , toutes les instances sauf les moins profondes sont redondantes.
Alors qu'une preuve de T13 nécessiterait une induction , l'intuition sous-jacente devrait être claire.
C2 ou son équivalent est nommé :
- "Génération" en LoF ;
- « Exclusion » dans Johnson (1892);
- "Pervasion" dans l'œuvre de William Bricken.
Peut-être la première instance d'un axiome ou d'une règle avec la puissance de C2 était la « règle de (De) Iteration », combinant T13 et AA = A , de CS Peirce de graphiques existentiels .
LoF affirme que la concaténation peut être lue comme une commutation et une association par défaut et n'a donc pas besoin d'être explicitement supposée ou démontrée. (Peirce a fait une affirmation similaire à propos de ses graphes existentiels .) Soit une période une notation temporaire pour établir le groupement. Cette concaténation commute et associe peut alors être démontrée à partir de :
- Initial AC.D = CD.A et la conséquence AA = A (Byrne 1946). Ce résultat est valable pour tous les réseaux , car AA = A est une conséquence facile de la loi d'absorption , qui est valable pour tous les réseaux ;
- Initiales AC.D = AD.C et J0 . Puisque J0 n'est valable que pour les réseaux avec une borne inférieure, cette méthode n'est valable que pour les réseaux bornés (qui incluent l' algèbre primaire et 2 ). La commutativité est triviale ; il suffit de définir A =
 . Associativité : AC.D = CA.D = CD.A = A.CD .
. Associativité : AC.D = CA.D = CD.A = A.CD .
Après avoir démontré l'associativité, la période peut être écartée.
Les initiales dans Meguire (2011) sont AC.D = CD.A , appelée B1 ; B2 , J0 ci-dessus ; B3 , J1a ci-dessus ; et B4 , C2. De par leur conception, ces initiales sont très similaires aux axiomes pour un groupe abélien , G1-G3 ci - dessous.
Théorie de la preuve
L' algèbre primaire contient trois sortes d'assertions prouvées :
- La conséquence est une équation algébrique primaire vérifiée par une démonstration . Une démonstration consiste en une séquence d' étapes , chaque étape étant justifiée par une conséquence initiale ou précédemment démontrée.
- Le théorème est un énoncé dans le métalangage vérifié par une preuve , c'est-à-dire un argument, formulé dans le métalangage, qui est accepté par les mathématiciens et les logiciens entraînés.
- Initiale , définie ci-dessus. Démonstrations et preuves invoquent une initiale comme s'il s'agissait d'un axiome.
La distinction entre conséquence et théorème vaut pour tous les systèmes formels, y compris les mathématiques et la logique, mais n'est généralement pas explicite. Une procédure de démonstration ou de décision peut être effectuée et vérifiée par ordinateur. La preuve d'un théorème ne peut pas être.
Laissez - A et B être algèbre primaire formules . Une démonstration de A = B peut se dérouler de deux manières :
- Modifiez A par étapes jusqu'à ce que B soit obtenu, ou vice versa ;
- Simplifier à la fois
 et
et 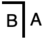 à
à  . C'est ce qu'on appelle un "calcul".
. C'est ce qu'on appelle un "calcul".
Une fois que A = B a été démontré, A = B peut être invoqué pour justifier les étapes des démonstrations ultérieures. les démonstrations et les calculs d' algèbre primaire ne nécessitent souvent pas plus que J1a , J2 , C2 , et les conséquences ![]() ( C3 dans LoF ),
( C3 dans LoF ), ![]() ( C1 ) et AA = A ( C5 ).
( C1 ) et AA = A ( C5 ).
La conséquence 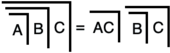 , C7' dans LoF , permet un algorithme , esquissé dans LoF s preuve de T14, qui transforme une formule algèbre primaire arbitraire en une formule équivalente dont la profondeur n'excède pas deux. Le résultat est une forme normale , l' analogue algébrique primaire de la forme normale conjonctive . LoF (T14-15) prouve la première algèbre analogique du bien connu algèbre de Boole théorème que chaque formule a une forme normale.
, C7' dans LoF , permet un algorithme , esquissé dans LoF s preuve de T14, qui transforme une formule algèbre primaire arbitraire en une formule équivalente dont la profondeur n'excède pas deux. Le résultat est une forme normale , l' analogue algébrique primaire de la forme normale conjonctive . LoF (T14-15) prouve la première algèbre analogique du bien connu algèbre de Boole théorème que chaque formule a une forme normale.
Soit A une sous - formule d'une formule B . Lorsqu'il est associé à C3 , J1a peut être considéré comme la condition de clôture des calculs : B est une tautologie si et seulement si A et ( A ) apparaissent tous les deux à la profondeur 0 de B . Une condition connexe apparaît dans certaines versions de la déduction naturelle . Une démonstration par calcul n'est souvent guère plus que :
- Invocation répétée de T13 pour éliminer les sous-formules redondantes ;
- Effacer toutes les sous-formules ayant la forme
 .
.
La dernière étape d'un calcul appelle toujours J1a .
LoF inclut de nouvelles preuves élégantes de la métathéorie standard suivante :
- Complétude : toutes les conséquences de l' algèbre primaire sont démontrables à partir des initiales (T17).
- Indépendance : J1 ne peut pas être démontré de J2 et vice versa (T18).
Que la logique phrastique soit complète est enseignée dans chaque premier cours universitaire de logique mathématique . Mais les cours universitaires d'algèbre booléenne mentionnent rarement la complétude de 2 .
Interprétations
Si les états Marqué et Non marqué sont lus comme les valeurs booléennes 1 et 0 (ou True et False ), l' algèbre primaire interprète 2 (ou la logique propositionnelle ). LoF montre comment l' algèbre primaire peut interpréter le syllogisme . Chacune de ces interprétations est discutée dans une sous-section ci-dessous. L' extension de l' algèbre primaire afin qu'il puisse interpréter la norme logique du premier ordre n'a pas encore fait, mais Peirce de bêta graphiques existentiels suggèrent que cette extension est possible.
Algèbre booléenne à deux éléments 2
L' algèbre primaire est une élégante notation minimaliste pour l' algèbre booléenne à deux éléments 2 . Laisser:
- Un booléen join (+) ou meet (×) interprète la concaténation ;
- Le complément de A interpréter
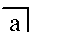
- 0 (1) interpréter la marque vide si join (meet) interprète la concaténation (car une opération binaire appliquée à zéro opérande peut être considérée comme étant égale à l' élément d'identité de cette opération ; ou pour le dire autrement, un opérande qui est manquant pourrait être considéré comme agissant par défaut comme l'élément d'identité).
Si join (meet) interprète AC , alors meet (join) interprète . Ainsi l' algèbre primaire et 2 sont isomorphes mais pour un détail : la complémentation de l' algèbre primaire peut être nulle, auquel cas elle dénote une valeur primitive. Modulo ce détail, 2 est un modèle de l'algèbre primaire. L'arithmétique primaire suggère l'axiomatisation arithmétique suivante de 2 : 1+1=1+0=0+1=1=~0, et 0+0=0=~1.
L' ensemble est le domaine booléen ou transporteur . Dans le langage de l'algèbre universelle , l' algèbre primaire est la structure algébrique de type . L' adéquation expressive du trait de Sheffer indique que l' algèbre primaire est également une algèbre de type . Dans les deux cas, les identités sont J1a, J0, C2 et ACD=CDA . Puisque l' algèbre primaire et 2 sont isomorphes , 2 peut être vu comme une algèbre de type . Cette description de 2 est plus simple que la classique, à savoir une algèbre de type .
![]()
![]()
Les deux interprétations possibles sont duelles au sens booléen. (En algèbre booléenne, l'échange de AND OR et 1 ↔ 0 dans une équation donne une équation également valable.) Les identités restent invariantes quelle que soit l'interprétation choisie, de sorte que les transformations ou les modes de calcul restent les mêmes ; seule l'interprétation de chaque forme serait différente. Exemple : J1a est ![]() . Interpréter la juxtaposition comme OU et
. Interpréter la juxtaposition comme OU et ![]() comme 1, cela se traduit par ce qui est vrai. En interprétant la juxtaposition comme AND et comme 0, cela se traduit par ce qui est également vrai (et le dual de ).
comme 1, cela se traduit par ce qui est vrai. En interprétant la juxtaposition comme AND et comme 0, cela se traduit par ce qui est également vrai (et le dual de ).
![]()
Logique des peines
Que la page blanche indique Faux , et qu'une Croix soit lue comme Non . Alors l'arithmétique primaire a la lecture propositionnelle suivante :
- = Faux
L' algèbre primaire interprète la logique phrastique comme suit. Une lettre représente une expression phrastique donnée. Ainsi:
|
, |
|
les deux interprètent A si et seulement si B ou A est équivalent à B . |
Ainsi, toute expression en logique propositionnelle a une traduction algébrique primaire . De manière équivalente, l' algèbre primaire interprète la logique phrastique. Étant donné une affectation de chaque variable aux états Marqué ou Non marqué, cette traduction algébrique primaire se réduit à une expression arithmétique primaire, qui peut être simplifiée. La répétition de cet exercice pour toutes les affectations possibles des deux valeurs primitives à chaque variable révèle si l'expression originale est tautologique ou satisfiable . C'est un exemple de procédure de décision , plus ou moins dans l'esprit des tables de vérité conventionnelles. Étant donné une formule algébrique primaire contenant N variables, cette procédure de décision nécessite de simplifier 2 N formules arithmétiques primaires. Pour une procédure de décision moins fastidieuse plus dans l'esprit de l'« analyse de la valeur de vérité » de Quine , voir Meguire (2003).
Schwartz (1981) a prouvé que l' algèbre primaire est équivalente — syntaxiquement , sémantiquement et théoriquement — au calcul propositionnel classique . De même, on peut montrer que l' algèbre primaire est syntaxiquement équivalente avec des expressions construites de la manière habituelle à partir des valeurs de vérité classiques true et false , des connecteurs logiques NON, OU et ET, et des parenthèses.
Interpréter l'État non marqué comme faux est totalement arbitraire ; cet état peut également être lu comme True . Tout ce qui est requis est que l'interprétation de la concaténation passe de OU à ET. SI A ALORS B se traduit maintenant par au ![]() lieu de
lieu de ![]() . Plus généralement, l' algèbre primaire est « auto- duale », ce qui signifie que toute formule d' algèbre primaire a deux lectures propositionnelles ou booléennes , chacune étant duelle de l'autre. Une autre conséquence de l'auto-dualité est la non-pertinence des lois de De Morgan ; ces lois sont intégrées dans la syntaxe de l' algèbre primaire dès le départ.
. Plus généralement, l' algèbre primaire est « auto- duale », ce qui signifie que toute formule d' algèbre primaire a deux lectures propositionnelles ou booléennes , chacune étant duelle de l'autre. Une autre conséquence de l'auto-dualité est la non-pertinence des lois de De Morgan ; ces lois sont intégrées dans la syntaxe de l' algèbre primaire dès le départ.
La vraie nature de la distinction entre l' algèbre primaire d' une part, et la logique 2 et propositionnelle d'autre part, émerge maintenant. Dans ces derniers formalismes, la complémentation / négation opérant sur « rien » n'est pas bien formée. Mais une croix vide est une expression algèbre primaire bien formée , dénotant l'état Marqué, une valeur primitive. Par conséquent, une croix non vide est un opérateur , tandis qu'une croix vide est un opérande car elle désigne une valeur primitive. Ainsi, l' algèbre primaire révèle que les concepts mathématiques jusqu'ici distincts d'opérateur et d'opérande ne sont en fait que des facettes différentes d'une seule action fondamentale, la réalisation d'une distinction.
Syllogismes
L'annexe 2 de LoF montre comment traduire les syllogismes et sorites traditionnels en algèbre primaire . Un syllogisme valide est simplement un syllogisme dont la traduction algébrique primaire se simplifie en une croix vide. Soit A * un littéral , c'est-à-dire soit A soit , indifféremment. Alors tout syllogisme qui n'exige pas qu'un ou plusieurs termes soient supposés non vides est l'une des 24 permutations possibles d'une généralisation de Barbara dont l' équivalent algèbre primaire est . Ces 24 permutations possibles incluent les 19 formes syllogistiques jugées valides dans la logique aristotélicienne et médiévale . Cette traduction d' algèbre primaire de la logique syllogistique suggère également que l' algèbre primaire peut interpréter la logique monadique et des termes , et que l' algèbre primaire a des affinités avec les schémas de termes booléens de Quine (1982 : Part II).
Un exemple de calcul
Le calcul suivant du théorème de Praeclarum non trivial de Leibniz illustre le pouvoir démonstratif de l' algèbre primaire . Soit C1 = A , C2 soit , C3 soit , J1a soit , et OI signifie que les variables et les sous-formules ont été réordonnées d'une manière que permettent la commutativité et l'associativité.
| [( P → R )∧( Q → S )]→[( P ∧ Q )→( R ∧ S )]. | Théorème du Praeclarum . | ||||||||||||||||||||||
|
traduction algèbre primaire | ||||||||||||||||||||||
|
C1. | ||||||||||||||||||||||
|
C1. | ||||||||||||||||||||||
|
OI. | ||||||||||||||||||||||
|
C2. | ||||||||||||||||||||||
|
OI. | ||||||||||||||||||||||
|
C2. | ||||||||||||||||||||||
|
OI. | ||||||||||||||||||||||
|
C2. | ||||||||||||||||||||||
|
C1. | ||||||||||||||||||||||
|
OI. | ||||||||||||||||||||||
|
J1a. | ||||||||||||||||||||||
|
OI. | ||||||||||||||||||||||
|
C3. |
Relation avec les magmas
L' algèbre primaire incarne un point noté par Huntington en 1933 : l'algèbre booléenne nécessite, en plus d'une opération unaire , une, et non deux, opérations binaires . D'où le fait rarement noté que les algèbres booléennes sont des magmas . (Les magmas étaient appelés groupoïdes jusqu'à ce que ce dernier terme soit approprié par la théorie des catégories .) Pour voir cela, notez que l' algèbre primaire est une commutative :
- Semi-groupe parce que la juxtaposition de l' algèbre primaire commute et s'associe ;
-
Monoïde avec élément d'identité
 , grâce à J0 .
, grâce à J0 .
Les groupes nécessitent également une opération unaire , appelée inverse , la contrepartie de groupe de la complémentation booléenne . Notons ![]() l'inverse de a . Notons
l'inverse de a . Notons ![]() l' élément d'identité de groupe . Alors les groupes et l' algèbre primaire ont les mêmes signatures , c'est-à-dire qu'ils sont tous deux des algèbres de type 〈2,1,0〉. D' où l' algèbre primaire est une algèbre limite . Les axiomes pour un groupe abélien , en notation aux frontières, sont :
l' élément d'identité de groupe . Alors les groupes et l' algèbre primaire ont les mêmes signatures , c'est-à-dire qu'ils sont tous deux des algèbres de type 〈2,1,0〉. D' où l' algèbre primaire est une algèbre limite . Les axiomes pour un groupe abélien , en notation aux frontières, sont :
A partir de G1 et G2 , la commutativité et l'associativité de la concaténation peuvent être dérivées, comme ci-dessus. Notez que G3 et J1a sont identiques. G2 et J0 seraient identiques si ![]() =
= ![]() remplacé A2 . C'est l'identité arithmétique qui définit la théorie des groupes, en notation aux frontières.
remplacé A2 . C'est l'identité arithmétique qui définit la théorie des groupes, en notation aux frontières.
L' algèbre primaire diffère d'un groupe abélien de deux manières :
- A partir de A2 , il en résulte que
 ≠
≠  . Si l' algèbre primaire était un groupe ,
. Si l' algèbre primaire était un groupe ,  =
=  tiendrait, et l'un de a = ou a = a devrait être une conséquence algèbre primaire . Notez que et sont des compléments mutuels d'algèbre primaire , comme l'exige la théorie des groupes, ce qui est vrai à la fois de la théorie des groupes et de l' algèbre primaire ;
tiendrait, et l'un de a = ou a = a devrait être une conséquence algèbre primaire . Notez que et sont des compléments mutuels d'algèbre primaire , comme l'exige la théorie des groupes, ce qui est vrai à la fois de la théorie des groupes et de l' algèbre primaire ;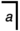




- C2 délimite le plus clairement l' algèbre primaire des autres magmas, car C2 permet de démontrer la loi d'absorption qui définit les réseaux , et la loi de distribution centrale à l'algèbre de Boole .
Les deux A2 et C2 suivi de B étant un de l » ensemble ordonné .
Équations du second degré (Chapitre 11)
Le chapitre 11 de LoF introduit des équations du second degré , composées de formules récursives qui peuvent être vues comme ayant une profondeur « infinie ». Certaines formules récursives simplifient l'état marqué ou non marqué. D'autres « oscillent » indéfiniment entre les deux états selon qu'une profondeur donnée est paire ou impaire. Plus précisément, certaines formules récursives peuvent être interprétées comme oscillant entre vrai et faux sur des intervalles de temps successifs, auquel cas une formule est réputée avoir une valeur de vérité « imaginaire ». Ainsi l'écoulement du temps peut être introduit dans l' algèbre primaire .
Turney (1986) montre comment ces formules récursives peuvent être interprétées via l' arithmétique récursive restreinte d' Alonzo Church (RRA). Church a introduit RRA en 1955 comme une formalisation axiomatique des automates finis . Turney (1986) présente une méthode générale pour traduire les équations du second degré en RRA de Church, illustrant sa méthode en utilisant les formules E1 , E2 et E4 au chapitre 11 de LoF . Cette traduction en RRA met en lumière les noms que Spencer-Brown a donnés à E1 et E4 , à savoir « mémoire » et « compteur ». Et ainsi ARR formalise précise LoF la notion « d'une valeur de vérité imaginaire.
Travaux connexes
Gottfried Leibniz , dans des mémorandums non publiés avant la fin du XIXe et le début du XXe siècle, a inventé la logique booléenne . Sa notation était isomorphe à celle de LoF : concaténation lue comme une conjonction , et « non-( X ) » lue comme le complément de X . La reconnaissance du rôle de pionnier de Leibniz dans la logique algébrique a été annoncée par Lewis (1918) et Rescher (1954). Mais une pleine appréciation des réalisations de Leibniz a dû attendre le travail de Wolfgang Lenzen, publié dans les années 1980 et passé en revue dans Lenzen (2004).
Charles Sanders Peirce (1839-1914) a anticipé l' algèbre primaire dans trois domaines de travail :
- Deux articles qu'il écrivit en 1886 proposèrent une algèbre logique n'employant qu'un seul symbole, la banderole , presque identique à la Croix de LoF . La sémantique de la banderole est identique à celle de la Croix, sauf que Peirce n'a jamais écrit de banderole sans rien en dessous. Un extrait de l'un de ces articles a été publié en 1976, mais ils n'ont été publiés dans leur intégralité qu'en 1993.
- Dans un article d'encyclopédie de 1902, Peirce a noté l'algèbre booléenne et la logique phrastique à la manière de cette entrée, sauf qu'il a utilisé deux styles de parenthèses, basculant entre '(', ')' et '[', ']' avec chaque incrément dans profondeur de la formule.
- La syntaxe de ses graphes existentiels alpha n'est qu'une concaténation , lue comme une conjonction , et une clôture par des ovales, lue comme une négation . Si la concaténation de l' algèbre primaire est lue comme une conjonction , alors ces graphiques sont isomorphes à l' algèbre primaire (Kauffman 2001).
Ironiquement, LoF cite le vol. 4 de Peirce's Collected Papers, la source des formalismes en (2) et (3) ci-dessus. (1)-(3) étaient pratiquement inconnus au moment où (années 1960) et à l'endroit où (Royaume-Uni) LoF a été écrit. La sémiotique de Peirce , sur laquelle LoF est muette, peut pourtant éclairer les aspects philosophiques de LoF .
Kauffman (2001) discute une autre notation proche de celle de LoF , celle d'un article de 1917 de Jean Nicod , disciple de Bertrand Russell .
Les formalismes ci-dessus sont, comme l' algèbre primaire , toutes les instances de mathématiques de frontière , c'est-à-dire des mathématiques dont la syntaxe est limitée aux lettres et aux crochets (dispositifs englobants). Une syntaxe minimaliste de cette nature est une "notation aux limites". La notation de limite est exempte de symboles d'opérateur infix , prefix ou postfix . Les accolades très connues ('{', '}') de la théorie des ensembles peuvent être vues comme une notation de frontière.
Les travaux de Leibniz, Peirce et Nicod sont innocents de la métathéorie, comme ils l'ont écrit avant l'article historique d' Emil Post en 1920 (que LoF cite), prouvant que la logique sententielle est complète, et avant que Hilbert et Łukasiewicz ne montrent comment prouver l' indépendance de l'axiome en utilisant modèles .
Craig (1979) a soutenu que le monde, et comment les humains perçoivent et interagissent avec ce monde, a une riche structure booléenne. Craig était un logicien orthodoxe et une autorité en logique algébrique .
Les sciences cognitives de deuxième génération ont émergé dans les années 1970, après l' écriture de LoF . Sur les sciences cognitives et leur pertinence pour l'algèbre booléenne, la logique et la théorie des ensembles , voir Lakoff (1987) (voir les entrées d'index sous « Exemples de schéma d'image : conteneur ») et Lakoff et Núñez (2001). Aucun des deux livres ne cite LoF .
Les biologistes et scientifiques cognitifs Humberto Maturana et son étudiant Francisco Varela discutent tous deux de LoF dans leurs écrits, qui identifient la "distinction" comme l'acte cognitif fondamental. La psychologue et scientifique cognitive de Berkeley Eleanor Rosch a beaucoup écrit sur la notion étroitement liée de catégorisation.
D'autres systèmes formels avec des affinités possibles avec l'algèbre primaire comprennent :
- Méréologie qui a typiquement une structure en treillis très similaire à celle de l'algèbre de Boole. Pour quelques auteurs, la méréologie est simplement un modèle de l'algèbre booléenne et donc aussi de l'algèbre primaire.
- Mereotopology , qui est intrinsèquement plus riche que l'algèbre booléenne;
- Le système de Whitehead (1934), dont la primitive fondamentale est "indication".
L'arithmétique et l'algèbre primaires sont un formalisme minimaliste pour la logique phrastique et l'algèbre booléenne. D'autres formalismes minimalistes ayant le pouvoir de la théorie des ensembles incluent :
- Le calcul lambda ;
- Logique combinatoire avec deux ( S et K ) voire un ( X ) combinateurs primitifs ;
- Logique mathématique faite avec simplement trois notions primitives : un connectif, NAND (dont la traduction algébrique primaire est ou, duellement, ), quantification universelle et une formule atomique binaire , dénotant l' appartenance à un ensemble . C'est le système de Quine (1951).
- Les graphes existentiels bêta , avec un seul prédicat binaire indiquant l'appartenance à un ensemble. Cela doit encore être exploré. Les graphiques alpha mentionnés ci-dessus sont un cas particulier des graphiques bêta .
Voir également
- Algèbre de Boole (Wikipédia en anglais simple)
- Algèbre de Boole (introduction)
- Algèbre booléenne (logique)
- Algèbre booléenne (structure)
- Algèbres booléennes définies canoniquement
- Logique booléenne
- Graphique entitatif
- Graphe existentiel
- Liste des sujets d'algèbre booléenne
- Calcul propositionnel
- Algèbre booléenne à deux éléments
Remarques
Les références
- Editions des Lois de la Forme :
- 1969. Londres : Allen & Unwin, couverture rigide.
- 1972. Crown Publishers, couverture rigide : ISBN 0-517-52776-6
- 1973. Bantam Books, livre de poche. ISBN 0-553-07782-1
- 1979. EP Dutton, livre de poche. ISBN 0-525-47544-3
- 1994. Portland OR : Cognizer Company, livre de poche. ISBN 0-9639899-0-1
- 1997 Traduction allemande, intitulée Gesetze der Form . Lübeck : Bohmeier Verlag. ISBN 3-89094-321-7
- 2008 Bohmeier Verlag, Leipzig, 5e édition internationale. ISBN 978-3-89094-580-4
- Bostock, David, 1997. Logique intermédiaire . Université d'Oxford. Presse.
- Byrne, Lee, 1946, "Deux formulations d'algèbre booléenne", Bulletin de l'American Mathematical Society : 268–71.
- Craig, Guillaume (1979). "La logique booléenne et le monde physique de tous les jours". Actes et adresses de l'American Philosophical Association . 52 (6) : 751-78. doi : 10.2307/3131383 . JSTOR 3131383 .
- David Gries et Schneider, FB, 1993. Une approche logique des mathématiques discrètes . Springer-Verlag.
- William Ernest Johnson , 1892, "Le calcul logique", Mind 1 (ns): 3-30.
- Louis H. Kauffman , 2001, " Les mathématiques de CS Peirce ", Cybernetics and Human Knowing 8 : 79-110.
- ------, 2006, " Reformuler le théorème des couleurs de la carte. "
- ------, 2006a. " Lois de la forme – Une exploration des mathématiques et des fondements. " Projet de livre (donc gros).
- Lenzen, Wolfgang, 2004, " Leibniz's Logic " dans Gabbay, D., et Woods, J., eds., The Rise of Modern Logic: From Leibniz to Frege (Manuel d'histoire de la logique – Vol. 3) . Amsterdam : Elsevier, 1-83.
- Lakoff, George , 1987. Les femmes, le feu et les choses dangereuses . Presse de l'Université de Chicago.
- -------- et Rafael E. Núñez , 2001. D'où viennent les mathématiques : Comment l'esprit incarné fait naître les mathématiques . Livres de base.
- Meguire, PG (2003). "Découverte de l'algèbre des limites : une notation simplifiée pour l'algèbre booléenne et les foncteurs de vérité". Journal international des systèmes généraux . 32 : 25-87. CiteSeerX 10.1.1.106.634 . doi : 10.1080/0308107031000075690 . S2CID 9460101 .
- --------, 2011. Algèbre des limites : une approche plus simple de la logique de base et de l'algèbre booléenne . VDM Publishing Ltd. ISBN 978-3639367492 . La source d'une grande partie de cette entrée, y compris la notation qui met entre parenthèses ce que LoF place sous une croix. Évite les aspects plus spéculatifs de LoF .
- Willard Quine , 1951. Logique mathématique , 2e éd. Presse de l'Université Harvard.
- --------, 1982. Methods of Logic , 4e éd. Presse de l'Université Harvard.
- Rescher, Nicolas (1954). « L'interprétation de Leibniz de ses calculs logiques » . Journal de logique symbolique . 18 (1) : 1–13. doi : 10.2307/2267644 . JSTOR 2267644 . S2CID 689315 .
- Schwartz, Daniel G. (1981). « Isomorphismes des lois de la forme de G. Spencer-Brown et du calcul de F. Varela pour l'auto-référence ». Journal international des systèmes généraux . 6 (4) : 239–55. doi : 10.1080/03081078108934802 .
- Turney, PD (1986). " Lois de la forme et automates finis ". Journal international des systèmes généraux . 12 (4) : 307-18. doi : 10.1080/03081078608934939 .
- AN Whitehead , 1934, "Indication, classes, nombre, validation", Mind 43 (ns): 281–97, 543. Les rectificatifs à la p. 543 sont nombreux et importants, et les réimpressions ultérieures de cet article ne les incorporent pas.
- Dirk Baecker (éd.) (1993), Kalkül der Form. Suhrkamp ; Dirk Baecker (éd.), Probleme der Form . Suhrkamp.
- Dirk Baecker (éd.) (1999), Problèmes de forme , Stanford University Press.
- Dirk Baecker (éd.) (2013), A Mathematics of Form, A Sociology of Observers , Cybernetics & Human Knowing, vol. 20, non. 3-4 .
Liens externes
- Laws of Form , archive du site de Richard Shoup.
- Discours de Spencer-Brown à Esalen, 1973. Les formes autoréférentielles sont introduites dans la section intitulée "Degré d'équations et théorie des types".
- Louis H. Kauffman , " Box Algebra, Boundary Mathematics, Logic, and Laws of Form. "
- Kissel, Matthias, " Une introduction non systématique mais facile à comprendre aux lois de la forme . "
- Le Forum des lois de la forme , où l'algèbre primaire et les formalismes associés sont discutés depuis 2002.
- Une rencontre avec GSB par Moshe Klein
- The Markable Mark , une introduction par étapes faciles aux idées des lois de la forme
- Le calcul BF et la racine carrée de la négation par Louis Kauffman et Arthur Collings ; il étend les Lois de la Forme en ajoutant une valeur logique imaginaire. (Les valeurs logiques imaginaires sont introduites au chapitre 11 du livre Laws of Form .)
- Cours sur les lois de la forme - un cours en ligne gratuit qui présente le corps principal du texte des lois de la forme par Leon Conrad, le dernier étudiant de Spencer-Brown, qui a étudié le travail avec l'auteur.

























