Espace (mathématiques) - Space (mathematics)

En mathématiques , un espace est un ensemble (parfois appelé univers ) avec une structure ajoutée .

Alors que les mathématiques modernes utilisent de nombreux types d'espaces, tels que des espaces euclidiens , espaces linéaires , espaces topologiques , les espaces de Hilbert , ou des espaces de probabilité , il ne définit pas la notion d ' « espace » lui - même.

Un espace se compose d'objets mathématiques sélectionnés qui sont traités comme des points, et de relations sélectionnées entre ces points. La nature des points peut être très variable : par exemple, les points peuvent être des éléments d'un ensemble, des fonctions sur un autre espace, ou des sous-espaces d'un autre espace. Ce sont les relations qui définissent la nature de l'espace. Plus précisément, les espaces isomorphes sont considérés comme identiques, où un isomorphisme entre deux espaces est une correspondance un à un entre leurs points qui préserve les relations. Par exemple, les relations entre les points d'un espace euclidien tridimensionnel sont uniquement déterminées par les axiomes d'Euclide, et tous les espaces euclidiens tridimensionnels sont considérés comme identiques.

Les notions topologiques telles que la continuité ont des définitions naturelles dans chaque espace euclidien. Cependant, la topologie ne distingue pas les lignes droites des lignes courbes, et la relation entre les espaces euclidiens et topologiques est donc « oublieuse ». Les relations de ce type sont traitées plus en détail dans la section "Types d'espaces" .

Il n'est pas toujours clair si un objet mathématique donné doit être considéré comme un "espace" géométrique ou une "structure" algébrique. Une définition générale de « structure », proposée par Bourbaki , englobe tous les types d'espaces courants, fournit une définition générale de l'isomorphisme et justifie le transfert de propriétés entre les structures isomorphes.

Histoire

Tableau 1 | Développement historique des concepts mathématiques

Classique	Moderne
les axiomes sont des implications évidentes des définitions	les axiomes sont conventionnels
les théorèmes sont la vérité objective absolue	les théorèmes sont des implications des axiomes correspondants
les relations entre les points, les lignes, etc. sont déterminées par leur nature	les relations entre les points, les lignes, etc. sont essentielles ; leur nature n'est pas
les objets mathématiques nous sont donnés avec leur structure	chaque théorie mathématique décrit ses objets par certaines de leurs propriétés
la géométrie correspond à une réalité expérimentale	la géométrie est une vérité mathématique
toutes les propriétés géométriques de l'espace découlent des axiomes	les axiomes d'un espace n'ont pas besoin de déterminer toutes les propriétés géométriques
la géométrie est une science autonome et vivante	la géométrie classique est un langage universel des mathématiques
l'espace est en trois dimensions	différents concepts de dimension s'appliquent à différents types d'espaces
l'espace est l'univers de la géométrie	les espaces ne sont que des structures mathématiques, ils se produisent dans diverses branches des mathématiques

Avant l'âge d'or de la géométrie

Dans les mathématiques grecques anciennes, "l'espace" était une abstraction géométrique de la réalité tridimensionnelle observée dans la vie quotidienne. Vers 300 avant JC, Euclide a donné des axiomes pour les propriétés de l'espace. Euclide a construit toutes les mathématiques sur ces fondements géométriques, allant jusqu'à définir des nombres en comparant les longueurs de segments de droite à la longueur d'un segment de référence choisi.

La méthode des coordonnées ( géométrie analytique ) a été adoptée par René Descartes en 1637. A cette époque, les théorèmes géométriques étaient traités comme des vérités objectives absolues connaissables par l'intuition et la raison, similaires aux objets des sciences naturelles ; et les axiomes ont été traités comme des implications évidentes des définitions.

Deux relations d'équivalence entre figures géométriques ont été utilisées : congruence et similarité . Les translations, les rotations et les réflexions transforment une figure en figures congruentes ; homothéties - en figures similaires. Par exemple, tous les cercles sont mutuellement similaires, mais les ellipses ne sont pas similaires aux cercles. Une troisième relation d'équivalence, introduite par Gaspard Monge en 1795, apparaît en géométrie projective : non seulement les ellipses, mais aussi les paraboles et les hyperboles, se transforment en cercles sous des transformations projectives appropriées ; ce sont tous des chiffres projectivement équivalents.

La relation entre les deux géométries, euclidienne et projective, montre que les objets mathématiques ne nous sont pas donnés avec leur structure . Au contraire, chaque théorie mathématique décrit ses objets par certaines de leurs propriétés, précisément celles qui sont posées comme axiomes aux fondements de la théorie.

Les distances et les angles ne peuvent pas apparaître dans les théorèmes de la géométrie projective, puisque ces notions ne sont ni mentionnées dans les axiomes de la géométrie projective ni définies à partir des notions qui y sont mentionnées. La question « quelle est la somme des trois angles d'un triangle » a un sens en géométrie euclidienne mais n'a pas de sens en géométrie projective.

Une situation différente est apparue au XIXe siècle : dans certaines géométries la somme des trois angles d'un triangle est bien définie mais différente de la valeur classique (180 degrés). La géométrie hyperbolique non euclidienne , introduite par Nikolai Lobatchevsky en 1829 et János Bolyai en 1832 (et Carl Friedrich Gauss en 1816, non publié) a déclaré que la somme dépend du triangle et est toujours inférieure à 180 degrés. Eugenio Beltrami en 1868 et Felix Klein en 1871 ont obtenu des « modèles » euclidiens de la géométrie hyperbolique non euclidienne, et ont ainsi complètement justifié cette théorie comme une possibilité logique.

Cette découverte força l'abandon des prétentions à la vérité absolue de la géométrie euclidienne. Il a montré que les axiomes ne sont pas « évidents », ni « les implications des définitions ». Ce sont plutôt des hypothèses. Dans quelle mesure correspondent-ils à une réalité expérimentale ? Cet important problème physique n'a plus rien à voir avec les mathématiques. Même si une « géométrie » ne correspond pas à une réalité expérimentale, ses théorèmes n'en restent pas moins des « vérités mathématiques ».

Un modèle euclidien d'une géométrie non-euclidienne est un choix de certains objets existant dans l'espace euclidien et de certaines relations entre ces objets qui satisfont tous les axiomes (et donc tous les théorèmes) de la géométrie non-euclidienne. Ces objets et relations euclidiens "jouent" la géométrie non-euclidienne comme des acteurs contemporains jouant une performance ancienne. Les acteurs peuvent imiter une situation qui ne s'est jamais produite dans la réalité. Les relations entre les acteurs sur la scène imitent les relations entre les personnages de la pièce. De même, les relations choisies entre les objets choisis du modèle euclidien imitent les relations non euclidiennes. Il montre que les relations entre les objets sont essentielles en mathématiques, alors que la nature des objets ne l'est pas.

L'âge d'or et après

Le mot « géométrie » (du grec ancien : géo- « terre », -métron « mesure ») signifiait initialement un moyen pratique de traiter les longueurs, les régions et les volumes dans l'espace dans lequel nous vivons, mais a ensuite été largement étendu (ainsi que comme la notion d'espace dont il est ici question).

Selon Bourbaki, la période entre 1795 ( Géométrie descriptive de Monge) et 1872 (le "programme Erlangen" de Klein) peut être qualifiée d'âge d'or de la géométrie. L'espace d'origine étudié par Euclide est maintenant appelé espace euclidien à trois dimensions . Son axiomatique, a commencé par Euclide il y a 23 siècles, a été réformé avec les axiomes de Hilbert , les axiomes de Tarski et les axiomes de Birkhoff . Ces systèmes d'axiomes décrivent l'espace via des notions primitives (telles que "point", "entre", "congruent") contraints par un certain nombre d' axiomes .

La géométrie analytique a fait de grands progrès et a réussi à remplacer les théorèmes de la géométrie classique par des calculs via des invariants de groupes de transformation. Depuis lors, les nouveaux théorèmes de la géométrie classique intéressent plus les amateurs que les mathématiciens professionnels. Cependant, l'héritage de la géométrie classique n'a pas été perdu. Selon Bourbaki, « dépassée dans son rôle de science autonome et vivante, la géométrie classique est ainsi transfigurée en un langage universel des mathématiques contemporaines ».

Simultanément, les nombres ont commencé à remplacer la géométrie en tant que fondement des mathématiques. Par exemple, dans l'essai de 1872 de Richard Dedekind Stetigkeit und irrationale Zahlen ( Continuité et nombres irrationnels ), il affirme que les points sur une ligne devraient avoir les propriétés des coupes de Dedekind , et que par conséquent une ligne était la même chose que l'ensemble des nombres réels . Dedekind prend soin de noter qu'il s'agit d'une hypothèse qui ne peut être prouvée. Dans les traitements modernes, l'affirmation de Dedekind est souvent considérée comme la définition d'une ligne, réduisant ainsi la géométrie à l'arithmétique. L'espace euclidien à trois dimensions est défini comme un espace affine dont l'espace vectoriel associé des différences de ses éléments est équipé d'un produit scalaire. Une définition « à partir de zéro », comme dans Euclide, est maintenant peu utilisée, car elle ne révèle pas la relation de cet espace avec d'autres espaces. De plus, un espace projectif tridimensionnel est maintenant défini comme l'espace de tous les sous-espaces unidimensionnels (c'est-à-dire des lignes droites passant par l'origine) d'un espace vectoriel quadridimensionnel. Ce déplacement des fondements nécessite un nouvel ensemble d'axiomes, et si ces axiomes sont adoptés, les axiomes classiques de la géométrie deviennent des théorèmes.

Un espace se compose désormais d'objets mathématiques sélectionnés (par exemple, des fonctions sur un autre espace, ou des sous-espaces d'un autre espace, ou simplement des éléments d'un ensemble) traités comme des points, et des relations sélectionnées entre ces points. Par conséquent, les espaces ne sont que des structures mathématiques de commodité. On peut s'attendre à ce que les structures appelées "espaces" soient perçues plus géométriquement que les autres objets mathématiques, mais ce n'est pas toujours vrai.

Selon la célèbre leçon inaugurale donnée par Bernhard Riemann en 1854, tout objet mathématique paramétré par n nombres réels peut être traité comme un point de l' espace à n dimensions de tous ces objets. Les mathématiciens contemporains suivent régulièrement cette idée et trouvent extrêmement suggestif d'utiliser la terminologie de la géométrie classique presque partout.

Les fonctions sont des objets mathématiques importants. Habituellement, ils forment des espaces fonctionnels de dimension infinie , comme l'a déjà noté Riemann et élaboré au 20e siècle par l'analyse fonctionnelle .

Taxonomie des espaces

Trois rangs taxonomiques

Si chaque type d'espace a sa propre définition, l'idée générale d'« espace » échappe à la formalisation. Certaines structures sont appelées espaces, d'autres non, sans critère formel. De plus, il n'y a pas de consensus sur l'idée générale de « structure ». Selon Pudlák, "Les mathématiques [...] ne peuvent pas être expliquées complètement par un seul concept tel que la structure mathématique. Néanmoins, l'approche structuraliste de Bourbaki est la meilleure que nous ayons." Nous reviendrons sur l'approche structuraliste de Bourbaki dans la dernière section "Espaces et structures", tandis que nous esquissons maintenant une possible classification des espaces (et des structures) dans l'esprit de Bourbaki.

Nous classons les espaces sur trois niveaux. Étant donné que chaque théorie mathématique décrit ses objets par certaines de leurs propriétés, la première question à se poser est : quelles propriétés ? Cela conduit au premier niveau de classification (supérieur). Au deuxième niveau, on prend en compte les réponses à des questions particulièrement importantes (parmi les questions qui font sens selon le premier niveau). Au troisième niveau de classification, on prend en compte les réponses à toutes les questions possibles.

Par exemple, la classification de niveau supérieur distingue les espaces euclidiens et projectifs , puisque la distance entre deux points est définie dans les espaces euclidiens mais indéfinie dans les espaces projectifs. Un autre exemple. La question « quelle est la somme des trois angles d'un triangle » a un sens dans un espace euclidien mais pas dans un espace projectif. Dans un espace non euclidien, la question a un sens mais reçoit une réponse différente, ce qui n'est pas une distinction de niveau supérieur.

De plus, la distinction entre un plan euclidien et un espace euclidien à trois dimensions n'est pas une distinction de niveau supérieur ; la question « quelle est la dimension » a un sens dans les deux cas.

La classification de second niveau distingue, par exemple, les espaces euclidiens et non euclidiens ; entre les espaces de dimension finie et de dimension infinie ; entre espaces compacts et non compacts, etc. Dans les termes de Bourbaki, la classification de second niveau est la classification par « espèces ». Contrairement à la taxonomie biologique, un espace peut appartenir à plusieurs espèces.

La classification de troisième niveau distingue, par exemple, des espaces de dimension différente, mais ne fait pas de distinction entre un plan d'un espace euclidien à trois dimensions, traité comme un espace euclidien à deux dimensions, et l'ensemble de toutes les paires de nombres réels, également traité comme un espace euclidien à deux dimensions. De même, il ne fait pas de distinction entre les différents modèles euclidiens du même espace non euclidien. Plus formellement, le troisième niveau classe les espaces jusqu'à l' isomorphisme . Un isomorphisme entre deux espaces est défini comme une correspondance bijective entre les points du premier espace et les points du deuxième espace, qui préserve toutes les relations stipulées selon le premier niveau. Les espaces mutuellement isomorphes sont considérés comme des copies d'un seul espace. Si l'un d'eux appartient à une espèce donnée, alors ils le font tous.

La notion d'isomorphisme éclaire la classification de niveau supérieur. Étant donné une correspondance bijective entre deux espaces de la même classe supérieure, on peut se demander s'il s'agit d'un isomorphisme ou non. Cette question n'a pas de sens pour deux espaces de classes différentes.

Un isomorphisme à lui-même est appelé un automorphisme. Les automorphismes d'un espace euclidien sont des déplacements, des rotations, des réflexions et des compositions de ceux-ci. L'espace euclidien est homogène dans le sens où chaque point peut être transformé en tout autre point par un automorphisme.

Les axiomes euclidiens ne laissent aucune liberté ; ils déterminent uniquement toutes les propriétés géométriques de l'espace. Plus exactement : tous les espaces euclidiens tridimensionnels sont mutuellement isomorphes. En ce sens, nous avons "l'espace euclidien tridimensionnel. Dans les termes de Bourbaki, la théorie correspondante est univalente . En revanche, les espaces topologiques sont généralement non isomorphes ; leur théorie est polyvalente . Une idée similaire se produit en logique mathématique : une théorie est dite catégorique si tous ses modèles de même cardinalité sont mutuellement isomorphes. Selon Bourbaki, l'étude des théories multivalentes est la caractéristique la plus frappante qui distingue les mathématiques modernes des mathématiques classiques.

Relations entre espèces d'espaces

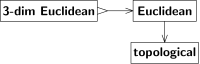
Les notions topologiques (continuité, convergence, ensembles ouverts, ensembles fermés etc.) sont définies naturellement dans tout espace euclidien. En d'autres termes, tout espace euclidien est aussi un espace topologique. Tout isomorphisme entre deux espaces euclidiens est aussi un isomorphisme entre les espaces topologiques correspondants (appelé « homéomorphisme »), mais l'inverse est faux : un homéomorphisme peut fausser les distances. Dans les termes de Bourbaki, « l'espace topologique » est une structure sous-jacente de la structure « de l'espace euclidien ». Des idées similaires se produisent dans la théorie des catégories : la catégorie des espaces euclidiens est une catégorie concrète sur la catégorie des espaces topologiques ; l' oublieux (ou « stripping ») foncteur cartes de la première catégorie à cette dernière catégorie.

Un espace euclidien tridimensionnel est un cas particulier d'espace euclidien. Dans les termes de Bourbaki, les espèces de l'espace euclidien à trois dimensions sont plus riches que les espèces de l'espace euclidien. De même, l'espèce de l'espace topologique compact est plus riche que l'espèce de l'espace topologique.

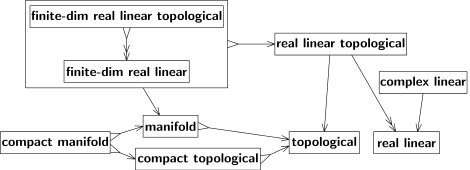
De telles relations entre les espèces d'espaces peuvent être exprimées de manière schématique comme le montre la Fig. 3. Une flèche de A à B signifie que chaque espace A est également un espace B, ou peut être traité comme un espace B, ou fournit un B -Espace, etc. le traitement a et B en tant que classes d'espaces , on peut interpréter la flèche comme une transition de a à B. (termes de Bourbaki, « procédure de déduction » d'un B-espace d'un a-espace. Pas tout à fait une fonction sauf si les classes A,B sont des ensembles ; cette nuance n'invalide pas ce qui suit.) Les deux flèches de la figure 3 ne sont pas inversibles, mais pour des raisons différentes.

Le passage de « euclidien » à « topologique » est oublieux. La topologie distingue le continu du discontinu, mais ne distingue pas le rectiligne du curviligne. L'intuition nous dit que la structure euclidienne ne peut pas être restaurée à partir de la topologie. Une preuve utilise un automorphisme de l'espace topologique (c'est-à-dire un auto-homéomorphisme ) qui n'est pas un automorphisme de l'espace euclidien (c'est-à-dire pas une composition de décalages, de rotations et de réflexions). Une telle transformation transforme la structure euclidienne donnée en une structure euclidienne (isomorphe mais) différente ; les deux structures euclidiennes correspondent à une seule structure topologique.

En revanche, le passage de « 3-dim euclidien » à « euclidien » n'est pas oublieux ; un espace euclidien n'a pas besoin d'être tridimensionnel, mais s'il se trouve à être tridimensionnel, il est à part entière, aucune structure n'est perdue. En d'autres termes, cette dernière transition est injective (un-à-un), tandis que la première transition n'est pas injective (plusieurs-à-un). Nous désignons les transitions injectives par une flèche avec une queue barbelée, "↣" plutôt que "→".

Les deux transitions ne sont pas surjectives , c'est-à-dire que tous les espaces B ne résultent pas d'un espace A. Premièrement, un espace euclidien à 3 dimensions est un cas particulier (non général) d'espace euclidien. Deuxièmement, une topologie d'un espace euclidien est un cas particulier de topologie (par exemple, il doit être non compact et connecté, etc.). Nous désignons les transitions surjectives par une flèche à deux pointes, "↠" plutôt que "→". Voir par exemple la figure 4 ; là, la flèche de "topologique linéaire réel" à "linéaire réel" est à deux pointes, puisque tout espace linéaire réel admet une (au moins une) topologie compatible avec sa structure linéaire.

Une telle topologie est non unique en général, mais unique lorsque l'espace linéaire réel est de dimension finie. Pour ces espaces, la transition est à la fois injective et surjective, c'est-à-dire bijective ; voir la flèche de « finite-dim real linear topological » à « finite-dim real linear" sur la figure 4. La transition inverse existe (et pourrait être représentée par une deuxième flèche vers l'arrière). Les deux espèces de structures sont donc équivalentes. En pratique, on ne fait aucune distinction entre espèces équivalentes de structures. Les structures équivalentes peuvent être traitées comme une structure unique, comme le montre un grand encadré sur la figure 4.

Les transitions désignées par les flèches obéissent à des isomorphismes. C'est-à-dire que deux espaces A isomorphes conduisent à deux espaces B isomorphes .

Le diagramme de la figure 4 est commutatif . C'est-à-dire que tous les chemins dirigés dans le diagramme avec les mêmes points de départ et de fin conduisent au même résultat. D'autres diagrammes ci-dessous sont également commutatifs, à l'exception des flèches en pointillés sur la figure 9. La flèche de « topologique » à « mesurable » est en pointillés pour la raison expliquée ici : « Pour transformer un espace topologique en un espace mesurable on lui donne une -algèbre. La -algèbre des ensembles de Borel est le choix le plus populaire, mais pas le seul." Une flèche pleine indique une transition répandue, dite "canonique" qui se suggère naturellement et est largement utilisée, souvent implicitement, par défaut. Par exemple, en parlant d'une fonction continue sur un espace euclidien, il n'est pas nécessaire de spécifier explicitement sa topologie. En fait, des topologies alternatives existent et sont parfois utilisées, par exemple, la topologie fine ; mais ceux-ci sont toujours spécifiés explicitement, car ils sont beaucoup moins notables que la topologie dominante. Une flèche en pointillé indique que plusieurs transitions sont en cours d'utilisation et qu'aucune n'est assez répandue.

Types d'espaces

Espaces linéaires et topologiques

Deux espaces de base sont les espaces linéaires (également appelés espaces vectoriels) et les espaces topologiques .

Les espaces linéaires sont de nature algébrique ; il existe des espaces linéaires réels (sur le corps des nombres réels ), des espaces linéaires complexes (sur le corps des nombres complexes ), et plus généralement des espaces linéaires sur n'importe quel corps. Tout espace linéaire complexe est aussi un espace linéaire réel (ce dernier est sous - jacent au premier), puisque chaque nombre réel est aussi un nombre complexe. Plus généralement, un espace vectoriel sur un champ a également la structure d'un espace vectoriel sur un sous-champ de ce champ. Les opérations linéaires, données dans un espace linéaire par définition, conduisent à des notions telles que lignes droites (et plans, et autres sous-espaces linéaires) ; lignes parallèles; ellipses (et ellipsoïdes). Cependant, il est impossible de définir des lignes orthogonales (perpendiculaires) ou de distinguer des cercles parmi des ellipses, car dans un espace linéaire, il n'y a pas de structure comme un produit scalaire qui pourrait être utilisé pour mesurer des angles. La dimension d'un espace linéaire est définie comme le nombre maximal de vecteurs linéairement indépendants ou, de manière équivalente, comme le nombre minimal de vecteurs qui s'étendent sur l'espace ; il peut être fini ou infini. Deux espaces linéaires sur le même champ sont isomorphes si et seulement s'ils sont de même dimension. Un espace linéaire complexe à n dimensions est également un espace linéaire réel à 2 n dimensions .

Les espaces topologiques sont de nature analytique . Les ensembles ouverts , donnés dans un espace topologique par définition, conduisent à des notions telles que les fonctions continues , les chemins, les cartes ; suites convergentes, limites ; intérieur, limite, extérieur. Cependant, continuité uniforme , ensembles bornés , séquences de Cauchy , fonctions différentiables (chemins, cartes) restent indéfinis. Les isomorphismes entre espaces topologiques sont traditionnellement appelés homéomorphismes ; ce sont des correspondances biunivoques continues dans les deux sens. L' intervalle ouvert (0,1) est homéomorphe à toute la droite réelle (−∞,∞) mais pas homéomorphe à l' intervalle fermé [0,1], ni à un cercle. La surface d'un cube est homéomorphe à une sphère (la surface d'une boule) mais pas homéomorphe à un tore. Les espaces euclidiens de dimensions différentes ne sont pas homéomorphes, ce qui semble évident, mais n'est pas facile à prouver. La dimension d'un espace topologique est difficile à définir ; la dimension inductive (basée sur l'observation que la dimension de la frontière d'une figure géométrique est généralement un de moins que la dimension de la figure elle-même) et la dimension de couverture de Lebesgue peuvent être utilisées. Dans le cas d'un espace euclidien de dimension n , les deux dimensions topologiques sont égales à n .

Chaque sous-ensemble d'un espace topologique est lui-même un espace topologique (en revanche, seuls les sous-ensembles linéaires d'un espace linéaire sont des espaces linéaires). Les espaces topologiques arbitraires, étudiés par la topologie générale (appelée aussi topologie des ensembles de points) sont trop divers pour une classification complète jusqu'à l'homéomorphisme. Les espaces topologiques compacts sont une classe importante d'espaces topologiques ("espèces" de ce "type"). Toute fonction continue est bornée sur un tel espace. L'intervalle fermé [0,1] et la droite réelle étendue [−∞,∞] sont compacts ; l'intervalle ouvert (0,1) et la ligne (−∞,∞) ne le sont pas. La topologie géométrique étudie les variétés (une autre "espèce" de ce "type"); ce sont des espaces topologiques localement homéomorphes aux espaces euclidiens (et satisfaisant quelques conditions supplémentaires). Les variétés de faible dimension sont complètement classées jusqu'à l'homéomorphisme.

Les structures linéaires et topologiques sous-tendent la structure de l' espace topologique linéaire (en d'autres termes, l'espace vectoriel topologique). Un espace topologique linéaire est à la fois un espace linéaire réel ou complexe et un espace topologique, de sorte que les opérations linéaires sont continues. Donc un espace linéaire qui est aussi topologique n'est pas en général un espace topologique linéaire.

Tout espace linéaire réel ou complexe de dimension finie est un espace topologique linéaire dans le sens où il porte une et une seule topologie qui en fait un espace topologique linéaire. Les deux structures, « espace linéaire réel ou complexe de dimension finie » et « espace topologique linéaire de dimension finie », sont donc équivalentes, c'est-à-dire mutuellement sous-jacentes. En conséquence, chaque transformation linéaire inversible d'un espace topologique linéaire de dimension finie est un homéomorphisme. Les trois notions de dimension (une algébrique et deux topologiques) concordent pour les espaces linéaires réels de dimension finie. Dans les espaces de dimension infinie, cependant, différentes topologies peuvent se conformer à une structure linéaire donnée, et les transformations linéaires inversibles ne sont généralement pas des homéomorphismes.

Espaces affines et projectifs

Il est commode d'introduire des espaces affines et projectifs au moyen d'espaces linéaires, comme suit. Un sous-espace linéaire à n dimensions d' un espace linéaire à ( n + 1) dimensions , étant lui-même un espace linéaire à n dimensions , n'est pas homogène ; il contient un point spécial, l'origine. En le décalant par un vecteur extérieur à celui-ci, on obtient un sous-espace affine à n dimensions . C'est homogène. Un espace affine n'a pas besoin d'être inclus dans un espace linéaire, mais est isomorphe à un sous-espace affine d'un espace linéaire. Tous les espaces affines de dimension n sont mutuellement isomorphes. Pour reprendre les mots de John Baez , "un espace affine est un espace vectoriel qui a oublié son origine". En particulier, tout espace linéaire est aussi un espace affine.

Étant donné un sous-espace affine de dimension n A dans un espace linéaire de dimension ( n +1) L , une droite dans A peut être définie comme l'intersection de A avec un sous -espace linéaire de L bidimensionnel qui coupe A : en d'autres termes , avec un plan passant par l'origine qui n'est pas parallèle à A . Plus généralement, un sous-espace affine de dimension k de A est l'intersection de A avec un sous-espace linéaire de dimension ( k +1) de L qui coupe A .

Chaque point du sous-espace affine A est l'intersection de A avec un sous -espace linéaire unidimensionnel de L . Cependant, certains sous - espaces à une dimension de L sont parallèles à A ; dans un certain sens, ils coupent A à l'infini. L'ensemble de tous les sous - espaces linéaires à une dimension d' un espace linéaire à ( n +1) dimension est, par définition, un espace projectif à n dimensions . Et le sous-espace affine A est intégré dans l'espace projectif en tant que sous-ensemble propre. Cependant, l'espace projectif lui-même est homogène. Une droite dans l'espace projectif correspond à un sous -espace linéaire à deux dimensions de l'espace linéaire à ( n +1) dimensions. Plus généralement, un sous-espace projectif de dimension k de l'espace projectif correspond à un sous-espace linéaire de dimension ( k +1) de l'espace linéaire de dimension ( n +1), et est isomorphe à l' espace projectif de dimension k .

Ainsi définis, les espaces affines et projectifs sont de nature algébrique ; elles peuvent être réelles, complexes, et plus généralement, sur n'importe quel domaine.

Tout espace affine ou projectif réel ou complexe est aussi un espace topologique. Un espace affine est une variété non compacte ; un espace projectif est une variété compacte. Dans un espace projectif réel une droite est homéomorphe à un cercle, donc compacte, contrairement à une droite dans un espace linéaire d'affine.

Espaces métriques et uniformes

Les distances entre les points sont définies dans un espace métrique . Les isomorphismes entre les espaces métriques sont appelés isométries. Tout espace métrique est aussi un espace topologique. Un espace topologique est dit métrisable s'il sous-tend un espace métrique. Toutes les variétés sont métrisables.

Dans un espace métrique, on peut définir des ensembles bornés et des suites de Cauchy. Un espace métrique est dit complet si toutes les suites de Cauchy convergent. Chaque espace incomplet est isométriquement intégré, en tant que sous-ensemble dense, dans un espace complet (l'achèvement). Chaque espace métrique compact est complet ; la vraie ligne est non compacte mais complète ; l'intervalle ouvert (0,1) est incomplet.

Tout espace euclidien est aussi un espace métrique complet. De plus, toutes les notions géométriques immanentes à un espace euclidien peuvent être caractérisées en fonction de sa métrique. Par exemple, le segment de droite reliant deux points donnés A et C est constitué de tous les points B tels que la distance entre A et C est égale à la somme de deux distances, entre A et B et entre B et C .

La dimension de Hausdorff (liée au nombre de petites boules qui couvrent l'ensemble donné) s'applique aux espaces métriques, et peut être non entière (en particulier pour les fractales ). Pour un espace euclidien de dimension n , la dimension de Hausdorff est égale à n .

Les espaces uniformes n'introduisent pas de distances, mais permettent toujours d'utiliser la continuité uniforme, les séquences de Cauchy (ou filtres ou réseaux ), la complétude et la complétion. Tout espace uniforme est aussi un espace topologique. Tout espace topologique linéaire (métrisable ou non) est aussi un espace uniforme, et est complet en dimension finie mais généralement incomplet en dimension infinie. Plus généralement, tout groupe topologique commutatif est aussi un espace uniforme. Un groupe topologique non commutatif, cependant, porte deux structures uniformes, l'une invariante à gauche, l'autre invariante à droite.

Espaces normés, de Banach, de produit interne et de Hilbert

Les vecteurs dans un espace euclidien forment un espace linéaire, mais chaque vecteur a aussi une longueur, en d'autres termes, la norme, . Un espace linéaire réel ou complexe doté d'une norme est un espace normé . Tout espace normé est à la fois un espace topologique linéaire et un espace métrique. Un espace de Banach est un espace normé complet. De nombreux espaces de séquences ou de fonctions sont des espaces de Banach de dimension infinie. ${\style d'affichage x}$${\style d'affichage \lVert x\rVert }$

L'ensemble de tous les vecteurs de norme inférieure à un est appelé la boule unité d'un espace normé. C'est un ensemble convexe, à symétrie centrale, généralement pas un ellipsoïde ; par exemple, il peut s'agir d'un polygone (dans le plan) ou, plus généralement, d'un polytope (en dimension finie arbitraire). La loi du parallélogramme (appelée aussi identité du parallélogramme)

${\displaystyle \lVert xy\rVert ^{2}+\lVert x+y\rVert ^{2}=2\lVert x\rVert ^{2}+2\lVert y\rVert ^{2}\ ,}$

échoue généralement dans les espaces normés, mais est valable pour les vecteurs dans les espaces euclidiens, ce qui résulte du fait que la norme euclidienne au carré d'un vecteur est son produit scalaire avec lui-même, . ${\displaystyle \lVert x\rVert ^{2}=(x,x)}$

Un espace produit interne est un espace linéaire réel ou complexe, doté d'une forme bilinéaire ou respectivement sesquilinéaire, satisfaisant certaines conditions et appelé produit interne. Chaque espace produit intérieur est également un espace normé. Un espace normé sous-tend un espace produit intérieur si et seulement s'il satisfait la loi du parallélogramme, ou de manière équivalente, si sa boule unité est un ellipsoïde. Les angles entre les vecteurs sont définis dans les espaces de produits internes. Un espace de Hilbert est défini comme un espace de produit interne complet. (Certains auteurs insistent sur le fait qu'il doit être complexe, d'autres admettent également de vrais espaces de Hilbert.) De nombreux espaces de séquences ou de fonctions sont des espaces de Hilbert de dimension infinie. Les espaces de Hilbert sont très importants pour la théorie quantique .

Tous les espaces de produits internes réels à n dimensions sont mutuellement isomorphes. On peut dire que l' espace euclidien à n dimensions est l' espace produit interne réel à n dimensions qui a oublié son origine.

Variétés lisses et riemanniennes

Les variétés lisses ne sont pas appelées "espaces", mais pourraient l'être. Chaque variété lisse est une variété topologique et peut être intégrée dans un espace linéaire de dimension finie. Les surfaces lisses dans un espace linéaire de dimension finie sont des variétés lisses : par exemple, la surface d'un ellipsoïde est une variété lisse, un polytope ne l'est pas. Les espaces linéaires, affines et projectifs réels ou complexes de dimension finie sont également des variétés lisses.

À chacun de ses points, un chemin lisse dans une variété lisse a un vecteur tangent qui appartient à l'espace tangent de la variété en ce point. Espaces tangents à un n -dimensionnelle lisse sont multiples n -dimensionnelle espaces linéaires. La différentielle d'une fonction lisse sur une variété lisse fournit une fonctionnelle linéaire sur l'espace tangent en chaque point.

Une variété riemannienne , ou espace de Riemann, est une variété lisse dont les espaces tangents sont dotés de produits internes satisfaisant certaines conditions. Les espaces euclidiens sont aussi des espaces de Riemann. Les surfaces lisses dans les espaces euclidiens sont des espaces de Riemann. Un espace hyperbolique non euclidien est aussi un espace de Riemann. Une courbe dans un espace de Riemann a une longueur, et la longueur de la courbe la plus courte entre deux points définit une distance, telle que l'espace de Riemann est un espace métrique. L'angle entre deux courbes se coupant en un point est l'angle entre leurs lignes tangentes.

En renonçant à la positivité des produits scalaires sur les espaces tangents, on obtient des espaces pseudo-Riemann , y compris les espaces lorentziens qui sont très importants pour la relativité générale .

Espaces mesurables, de mesure et de probabilité

En renonçant aux distances et aux angles tout en conservant les volumes (des corps géométriques), on accède à la théorie de la mesure . Outre le volume, une mesure généralise les notions de distribution d'aire, de longueur, de masse (ou de charge), mais aussi de distribution de probabilité, selon l' approche d' Andrey Kolmogorov en théorie des probabilités .

Un "corps géométrique" des mathématiques classiques est beaucoup plus régulier qu'un simple ensemble de points. La limite du corps est de volume nul. Ainsi, le volume du corps est le volume de son intérieur, et l'intérieur peut être épuisé par une suite infinie de cubes. En revanche, la frontière d'un ensemble arbitraire de points peut être de volume non nul (un exemple : l'ensemble de tous les points rationnels à l'intérieur d'un cube donné). La théorie de la mesure a réussi à étendre la notion de volume à une vaste classe d'ensembles, les ensembles dits mesurables . En effet, les ensembles non mesurables n'apparaissent presque jamais dans les applications.

Les ensembles mesurables, donnés dans un espace mesurable par définition, conduisent à des fonctions et des cartes mesurables. Afin de transformer un espace topologique en un espace mesurable on le dote d'une -algèbre. La -algèbre des ensembles de Borel est le choix le plus populaire, mais pas le seul. ( Baire ensembles , ensembles mesurables universellement , etc, sont également utilisés parfois.) La topologie est pas déterminée uniquement par le Borel de-algèbre; par exemple, la topologie normale et la topologie faible sur un espace de Hilbert séparable conduisent à la même σ-algèbre de Borel . Pas tous les σ-algèbre est la Borel σ-algèbre d' une certaine topologie. En fait, une -algèbre peut être générée par une collection donnée d'ensembles (ou de fonctions) indépendamment de toute topologie. Chaque sous-ensemble d'un espace mesurable est lui-même un espace mesurable.

Les espaces mesurables standard (également appelés espaces de Borel standard ) sont particulièrement utiles en raison d'une certaine similitude avec les espaces compacts (voir EoM ). Chaque application mesurable bijective entre des espaces mesurables standard est un isomorphisme ; c'est-à-dire que le mappage inverse est également mesurable. Et une correspondance entre de tels espaces est mesurable si et seulement si son graphe est mesurable dans l'espace produit. De même, toute application continue bijective entre des espaces métriques compacts est un homéomorphisme ; c'est-à-dire que l'application inverse est également continue. Et une application entre de tels espaces est continue si et seulement si son graphe est fermé dans l'espace produit.

Tout ensemble de Borel dans un espace euclidien (et plus généralement, dans un espace métrique complet séparable), doté de la -algèbre de Borel , est un espace mesurable standard. Tous les espaces mesurables standard innombrables sont mutuellement isomorphes.

Un espace de mesure est un espace mesurable doté d'une mesure. Un espace euclidien avec la mesure de Lebesgue est un espace de mesure. La théorie de l'intégration définit l'intégrabilité et les intégrales de fonctions mesurables sur un espace de mesure.

Les ensembles de mesure 0, appelés ensembles nuls, sont négligeables. En conséquence, un « isomorphisme mod 0 » est défini comme un isomorphisme entre des sous-ensembles de mesure complète (c'est-à-dire avec un complément négligeable).

Un espace de probabilité est un espace de mesure tel que la mesure de tout l'espace est égale à 1. Le produit de toute famille (finie ou non) d'espaces de probabilité est un espace de probabilité. En revanche, pour les espaces de mesure en général, seul le produit d'un nombre fini d'espaces est défini. En conséquence, il existe de nombreuses mesures de probabilité de dimension infinie (en particulier, les mesures gaussiennes ), mais pas de mesures de Lebesgue de dimension infinie.

Les espaces de probabilité standard sont particulièrement utiles . Sur un espace de probabilité standard, une espérance conditionnelle peut être traitée comme l'intégrale sur la mesure conditionnelle ( probabilités conditionnelles régulières , voir aussi désintégration de la mesure ). Étant donné deux espaces de probabilité standard, chaque homomorphisme de leurs algèbres de mesures est induit par une carte préservant les mesures. Chaque mesure de probabilité sur un espace mesurable standard conduit à un espace de probabilité standard. Le produit d'une suite (finie ou non) d'espaces de probabilité standard est un espace de probabilité standard. Tous les espaces de probabilité standard non atomiques sont mutuellement isomorphes mod 0 ; l'un d'eux est l'intervalle (0,1) avec la mesure de Lebesgue.

Ces espaces sont moins géométriques. En particulier, la notion de dimension, applicable (sous une forme ou une autre) à tous les autres espaces, ne s'applique pas aux espaces mesurables, de mesure et de probabilité.

Géométrie non commutative

L'étude théorique du calcul, connue sous le nom d' analyse mathématique , a conduit au début du 20e siècle à la considération d'espaces linéaires de fonctions à valeur réelle ou à valeur complexe. Les premiers exemples en étaient les espaces fonctionnels , chacun adapté à sa propre classe de problèmes. Ces exemples partageaient de nombreuses caractéristiques communes, et ces caractéristiques ont rapidement été résumées dans des espaces de Hilbert, des espaces de Banach et des espaces vectoriels topologiques plus généraux. Il s'agissait d'une boîte à outils puissante pour la solution d'un large éventail de problèmes mathématiques.

L'information la plus détaillée était portée par une classe d'espaces appelés algèbres de Banach . Ce sont des espaces de Banach avec une opération de multiplication continue. Un premier exemple important était l'algèbre de Banach de fonctions mesurables essentiellement bornées sur un espace de mesure X . Cet ensemble de fonctions est un espace de Banach sous addition ponctuelle et multiplication scalaire. Avec l'opération de multiplication ponctuelle, il devient un type spécial d'espace de Banach, maintenant appelé algèbre de von Neumann commutative . La multiplication ponctuelle détermine une représentation de cette algèbre sur l'espace de Hilbert des fonctions carrées intégrables sur X . Une première observation de John von Neumann était que cette correspondance fonctionnait également à l'envers : étant donné quelques hypothèses techniques légères, une algèbre commutative de von Neumann avec une représentation sur un espace de Hilbert détermine un espace de mesure, et ces deux constructions (d'une algèbre de von Neumann plus une représentation et d'un espace de mesure) sont mutuellement inverses.

Von Neumann a alors proposé que les algèbres de von Neumann non commutatives aient une signification géométrique, tout comme le font les algèbres de von Neumann commutatives. Avec Francis Murray , il a produit une classification des algèbres de von Neumann. La construction intégrale directe montre comment décomposer n'importe quelle algèbre de von Neumann en une collection d'algèbres plus simples appelées facteurs . Von Neumann et Murray ont classé les facteurs en trois types. Le type I était presque identique au cas commutatif. Les types II et III présentaient de nouveaux phénomènes. Une algèbre de type II de von Neumann a déterminé une géométrie avec la particularité que la dimension pouvait être n'importe quel nombre réel non négatif, pas seulement un entier. Les algèbres de type III étaient celles qui n'étaient ni de type I ni de type II, et après plusieurs décennies d'efforts, il s'est avéré qu'elles étaient étroitement liées aux facteurs de type II.

Une approche légèrement différente de la géométrie des espaces fonctionnels s'est développée en même temps que les travaux de von Neumann et Murray sur la classification des facteurs. Cette approche est la théorie des C*-algèbres . Ici, l'exemple motivant est la C*-algèbre , où X est un espace topologique de Hausdorff localement compact. Par définition, il s'agit de l'algèbre des fonctions continues à valeurs complexes sur X qui disparaissent à l'infini (ce qui signifie grosso modo que plus vous vous éloignez d'un point choisi, plus la fonction se rapproche de zéro) avec les opérations d'addition et de multiplication ponctuelles. Le théorème de Gelfand-Naimark impliquait qu'il existe une correspondance entre les C*-algèbres commutatives et les objets géométriques : Chaque C*-algèbre commutative est de la forme pour un espace de Hausdorff localement compact X . Par conséquent, il est possible d'étudier les espaces de Hausdorff localement compacts uniquement en termes de C*-algèbres commutatives. La géométrie non-commutative s'en inspire pour l'étude des C*-algèbres non-commutatives : s'il existait un « espace non-commutatif X », alors ce serait une C*-algèbre non-commutative ; si en plus le théorème de Gelfand-Naimark s'appliquait à ces objets inexistants, alors les espaces (commutatifs ou non) seraient les mêmes que les C*-algèbres ; ainsi, faute d'une approche directe de la définition d'un espace non-commutatif, un espace non-commutatif est défini comme une C*-algèbre non-commutative . De nombreux outils géométriques standard peuvent être reformulés en termes de C*-algèbres, ce qui donne des techniques d'inspiration géométrique pour étudier les C*-algèbres non commutatives . ${\style d'affichage C_{0}(X)}$${\style d'affichage C_{0}(X)}$${\style d'affichage C_{0}(X)}$

Ces deux exemples sont maintenant des cas d'un champ appelé géométrie non commutative . Les exemples spécifiques d'algèbres de von Neumann et d'algèbres C* sont respectivement appelés théorie de la mesure non commutative et topologie non commutative. La géométrie non commutative n'est pas simplement une poursuite de la généralité pour elle-même et n'est pas seulement une curiosité. Des espaces non commutatifs naissent naturellement, voire inévitablement, de certaines constructions. Par exemple, considérons les pavages non périodiques de Penrose de l'avion par des cerfs-volants et des fléchettes. C'est un théorème que, dans un tel pavage, chaque parcelle finie de cerfs-volants et de fléchettes apparaît infiniment souvent. En conséquence, il n'y a aucun moyen de distinguer deux pavages de Penrose en regardant une partie finie. Cela rend impossible d'affecter à l'ensemble de tous les pavages une topologie au sens traditionnel du terme. Malgré cela, les pavages de Penrose déterminent une C*-algèbre non commutative , et par conséquent ils peuvent être étudiés par les techniques de la géométrie non commutative. Un autre exemple, et d'un grand intérêt en géométrie différentielle , vient des feuilletages de variétés. Ce sont des façons de diviser la variété en sous-variétés de plus petite dimension appelées feuilles , dont chacune est localement parallèle aux autres à proximité. L'ensemble de toutes les feuilles peut être transformé en un espace topologique. Cependant, l'exemple d'une rotation irrationnelle montre que cet espace topologique peut être inaccessible aux techniques de la théorie de la mesure classique. Cependant, il existe une algèbre de von Neumann non commutative associée à l'espace foliaire d'un feuilletage, et encore une fois, cela donne à un espace autrement inintelligible une bonne structure géométrique.

Schémas

La géométrie algébrique étudie les propriétés géométriques des équations polynomiales . Les polynômes sont un type de fonction défini à partir des opérations arithmétiques de base d'addition et de multiplication. Pour cette raison, ils sont étroitement liés à l'algèbre. La géométrie algébrique offre un moyen d'appliquer des techniques géométriques à des questions d'algèbre pure, et vice versa.

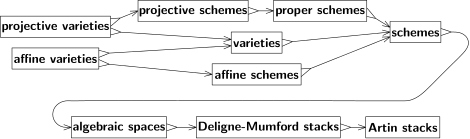
Avant les années 1940, la géométrie algébrique fonctionnait exclusivement sur les nombres complexes, et la variété la plus fondamentale était l'espace projectif. La géométrie de l'espace projectif est étroitement liée à la théorie de la perspective , et son algèbre est décrite par des polynômes homogènes . Toutes les autres variétés ont été définies comme des sous-ensembles de l'espace projectif. Les variétés projectives étaient des sous-ensembles définis par un ensemble de polynômes homogènes. À chaque point de la variété projective, tous les polynômes de l'ensemble devaient être égaux à zéro. Le complément de l'ensemble zéro d'un polynôme linéaire est un espace affine, et une variété affine était l'intersection d'une variété projective avec un espace affine.

André Weil a vu que le raisonnement géométrique pouvait parfois être appliqué dans des situations de théorie des nombres où les espaces en question pouvaient être discrets ou même finis. Dans la poursuite de cette idée, Weil a réécrit les fondements de la géométrie algébrique, libérant à la fois la géométrie algébrique de sa dépendance aux nombres complexes et introduisant des variétés algébriques abstraites qui n'étaient pas intégrées dans l'espace projectif. Celles-ci sont maintenant simplement appelées variétés .

Le type d'espace qui sous-tend la géométrie algébrique la plus moderne est encore plus général que les variétés algébriques abstraites de Weil. Il a été introduit par Alexander Grothendieck et s'appelle un schéma . L'une des motivations de la théorie des schémas est que les polynômes sont exceptionnellement structurés parmi les fonctions et que les variétés algébriques sont par conséquent rigides. Cela pose des problèmes lorsqu'on essaie d'étudier des situations dégénérées. Par exemple, presque n'importe quelle paire de points sur un cercle détermine une ligne unique appelée ligne sécante, et lorsque les deux points se déplacent autour du cercle, la ligne sécante varie continuellement. Cependant, lorsque les deux points entrent en collision, la ligne sécante dégénère en une ligne tangente. La ligne tangente est unique, mais la géométrie de cette configuration - un seul point sur un cercle - n'est pas assez expressive pour déterminer une ligne unique. L'étude de situations comme celle-ci nécessite une théorie capable d'attribuer des données supplémentaires à des situations dégénérées.

L'un des éléments constitutifs d'un schéma est un espace topologique. Les espaces topologiques ont des fonctions continues, mais les fonctions continues sont trop générales pour refléter la structure algébrique sous-jacente d'intérêt. L'autre ingrédient d'un schéma est donc une gerbe sur l'espace topologique, appelée « gerbe de structure ». Sur chaque sous-ensemble ouvert de l'espace topologique, le faisceau spécifie une collection de fonctions, appelées « fonctions régulières ». L'espace topologique et le faisceau de structure doivent satisfaire ensemble des conditions qui signifient que les fonctions proviennent d'opérations algébriques.

Comme les variétés, les schèmes sont définis comme des espaces modélisés localement sur un espace familier. Dans le cas des variétés, l'espace familier est l'espace euclidien. Pour un schéma, les modèles locaux sont appelés schémas affines . Les schémas affines fournissent un lien direct entre la géométrie algébrique et l' algèbre commutative . Les objets fondamentaux d'étude en algèbre commutative sont les anneaux commutatifs . Si est un anneau commutatif, alors il existe un schéma affine correspondant qui traduit la structure algébrique de en géométrie. Inversement, tout schéma affine détermine un anneau commutatif, à savoir l'anneau des sections globales de son faisceau de structure. Ces deux opérations étant mutuellement inverses, les schémas affines fournissent un nouveau langage pour étudier les questions d'algèbre commutative. Par définition, chaque point d'un schéma a un voisinage ouvert qui est un schéma affine. ${\style d'affichage R}$${\displaystyle \operatorname {Spec} R}$${\style d'affichage R}$

Il existe de nombreux schémas qui ne sont pas affines. En particulier, les espaces projectifs satisfont à une condition appelée propriété qui est analogue à la compacité. Les schémas affines ne peuvent pas être appropriés (sauf dans des situations triviales comme lorsque le schéma n'a qu'un seul point), et donc aucun espace projectif n'est un schéma affine (sauf pour les espaces projectifs de dimension zéro). Les schémas projectifs, c'est-à-dire ceux qui apparaissent comme des sous-schémas fermés d'un espace projectif, sont la famille de schémas la plus importante.

Plusieurs généralisations de schémas ont été introduites. Michael Artin a défini un espace algébrique comme le quotient d'un schéma par les relations d'équivalence qui définissent les morphismes étales . Les espaces algébriques conservent bon nombre des propriétés utiles des schémas tout en étant plus flexibles. Par exemple, le théorème de Keel-Mori peut être utilisé pour montrer que de nombreux espaces de modules sont des espaces algébriques.

Plus général qu'un espace algébrique est une pile Deligne-Mumford . Les piles DM sont similaires aux schémas, mais elles permettent des singularités qui ne peuvent pas être décrites uniquement en termes de polynômes. Ils jouent le même rôle pour les schémas que les orbifolds font pour les variétés . Par exemple, le quotient du plan affine par un groupe fini de rotations autour de l'origine donne un empilement de Deligne-Mumford qui n'est pas un schéma ou un espace algébrique. Loin de l'origine, le quotient par l'action de groupe identifie des ensembles finis de points également espacés sur un cercle. Mais à l'origine, le cercle n'est constitué que d'un seul point, l'origine elle-même, et l'action de groupe fixe ce point. Dans la pile DM du quotient, cependant, ce point vient avec les données supplémentaires d'être un quotient. Ce type de structure raffinée est utile dans la théorie des espaces de modules, et en fait, il a été introduit à l'origine pour décrire les modules de courbes algébriques .

Une autre généralisation sont les piles algébriques , également appelées piles d'Artin. Les piles DM sont limitées aux quotients par des actions de groupe fini. Bien que cela suffise pour de nombreux problèmes de la théorie des modules, c'est trop restrictif pour d'autres, et les piles d'Artin permettent des quotients plus généraux.

Topoi

Dans les travaux de Grothendieck sur les conjectures de Weil , il a introduit un nouveau type de topologie maintenant appelé topologie de Grothendieck . Un espace topologique (au sens ordinaire du terme) axiomatise la notion de « proximité », faisant en sorte que deux points soient proches si et seulement s'ils se trouvent dans plusieurs des mêmes ensembles ouverts. En revanche, une topologie de Grothendieck axiomatise la notion de « recouvrement ». Une couverture d'un espace est une collection de sous-espaces qui contiennent conjointement toutes les informations de l'espace ambiant. Puisque les faisceaux sont définis en termes de revêtements, une topologie de Grothendieck peut également être vue comme une axiomatisation de la théorie des faisceaux.

Les travaux de Grothendieck sur ses topologies l'ont conduit à la théorie des topoi . Dans ses mémoires Récoltes et Semailles , il les appelle sa « conception la plus vaste ». Un faisceau (soit sur un espace topologique soit par rapport à une topologie de Grothendieck) est utilisé pour exprimer des données locales. La catégorie de toutes les gerbes porte toutes les manières possibles d'exprimer des données locales. Les espaces topologiques étant construits à partir de points, qui sont eux-mêmes une sorte de données locales, la catégorie des faisceaux peut donc être utilisée en remplacement de l'espace d'origine. Grothendieck a donc défini un topos comme une catégorie de gerbes et étudié les topoi comme des objets d'intérêt à part entière. Ceux-ci sont maintenant appelés Grothendieck topoi .

Chaque espace topologique détermine un topos, et vice versa. Il existe des espaces topologiques où la prise du topos associé fait perdre de l'information, mais ceux-ci sont généralement considérés comme pathologiques. (Une condition nécessaire et suffisante est que l'espace topologique soit un espace sobre .) A l'inverse, il existe des topoi dont les espaces topologiques associés ne capturent pas le topos originel. Mais, loin d'être pathologiques, ces topoi peuvent présenter un grand intérêt mathématique. Par exemple, la théorie de la cohomologie étale de Grothendieck (qui a finalement conduit à la preuve des conjectures de Weil) peut être formulée comme une cohomologie dans le topos étale d'un schéma, et ce topos ne vient pas d'un espace topologique.

Les espaces topologiques conduisent en effet à des topoi très particuliers appelés locales . L'ensemble des sous-ensembles ouverts d'un espace topologique détermine un treillis . Les axiomes pour un espace topologique font de ces réseaux des algèbres de Heyting complètes . La théorie des lieux prend cela comme point de départ. Un lieu est défini comme une algèbre de Heyting complète, et les propriétés élémentaires des espaces topologiques sont réexprimées et réprouvées en ces termes. Le concept d'un lieu s'avère plus général que celui d'un espace topologique, dans la mesure où chaque espace topologique sobre détermine un lieu unique, mais de nombreux lieux intéressants ne proviennent pas d'espaces topologiques. Parce que les locales n'ont pas besoin d'avoir des points, l'étude des locales est appelée en plaisantant topologie inutile .

Les topoi présentent également des liens profonds avec la logique mathématique. Chaque topos de Grothendieck a une gerbe spéciale appelée classificateur de sous-objet. Ce classificateur de sous-objet fonctionne comme l'ensemble de toutes les valeurs de vérité possibles. Dans les topos d'ensembles, le classificateur de sous-objet est l'ensemble , correspondant à "False" et "True". Mais dans d'autres topoi, le classificateur de sous-objet peut être beaucoup plus compliqué. Lawvere et Tierney ont reconnu que l'axiomatisation du classificateur de sous-objets donnait un type plus général de topos, maintenant connu sous le nom de topos élémentaire , et que les topoi élémentaires étaient des modèles de logique intuitionniste . En plus de fournir un moyen puissant d'appliquer des outils de la logique à la géométrie, cela a rendu possible l'utilisation de méthodes géométriques en logique. ${\style d'affichage \{0,1\}}$

Espaces et structures

Selon Kevin Carlson,

Aucun de ces mots ["espace" et "structure"] n'a de définition mathématique unique. Les mots anglais peuvent être utilisés essentiellement dans toutes les mêmes situations, mais vous pensez souvent qu'un "espace" est plus géométrique et une "structure" plus algébrique. [...] Vous pourriez donc considérer les "structures" comme des endroits où nous faisons de l'algèbre, et les "espaces" comme des endroits où nous faisons de la géométrie. Ensuite, beaucoup de grandes mathématiques sont venues du passage des structures aux espaces et vice versa, comme lorsqu'on regarde le groupe fondamental d'un espace topologique ou le spectre d'un anneau . Mais au final, la distinction n'est ni dure ni rapide et ne va pas loin : beaucoup de choses sont évidemment à la fois des structures et des espaces, certaines ne le sont évidemment pas non plus, et certaines personnes pourraient bien être en désaccord avec tout ce que j'ai dit ici.

Néanmoins, une définition générale de la « structure » a été proposée par Bourbaki ; il embrasse tous les types d'espaces mentionnés ci-dessus, (presque ?) tous les types de structures mathématiques utilisées jusqu'à présent, et plus encore. Il fournit une définition générale de l'isomorphisme et justifie le transfert de propriétés entre structures isomorphes. Cependant, il n'a jamais été utilisé activement dans la pratique mathématique (pas même dans les traités mathématiques écrits par Bourbaki lui-même). Voici les dernières phrases d'une critique par Robert Reed d'un livre de Leo Corry :

Corry ne semble pas sentir que toute définition formelle de la structure pourrait rendre justice à l'utilisation du concept dans la pratique mathématique réelle [...] point de vue de Corry pourrait se résumer comme la conviction que la « structure » fait essentiellement référence à une façon de faire les mathématiques , et est donc un concept probablement tout aussi loin d'être précisément définissable que l'artefact culturel des mathématiques elles-mêmes.

Pour plus d'informations sur les structures mathématiques, voir Wikipedia : structure mathématique , définitions équivalentes des structures mathématiques et transport de la structure .

La distinction entre « espaces » géométriques et « structures » algébriques est parfois claire, parfois insaisissable. Clairement, les groupes sont algébriques, tandis que les espaces euclidiens sont géométriques. Les modules sur les anneaux sont aussi algébriques que les groupes. En particulier, lorsque l' anneau apparaît comme un champ , le module apparaît comme un espace linéaire ; est-ce algébrique ou géométrique ? En particulier, lorsqu'il est de dimension finie, sur des nombres réels, et doté du produit scalaire , il devient espace euclidien ; maintenant géométrique. Le champ (algébrique ?) des nombres réels est le même que la droite (géométrique ?) réelle . Sa clôture algébrique , le corps (algébrique ?) des nombres complexes , est la même que le plan complexe (géométrique ?) . C'est d'abord « un lieu où l'on fait de l' analyse » (plutôt que de l'algèbre ou de la géométrie).

Chaque espace traité dans la section " Types d'espaces " ci-dessus, à l'exception des sous- sections " Géométrie non commutative ", " Schémas " et " Topoi ", est un ensemble (le " ensemble de base principal " de la structure, selon Bourbaki) doté de une structure supplémentaire; les éléments de l'ensemble de base sont généralement appelés "points" de cet espace. En revanche, les éléments de (l'ensemble de base d') une structure algébrique ne sont généralement pas appelés "points".

Cependant, on utilise parfois plus d'un ensemble de base principal. Par exemple, la géométrie projective bidimensionnelle peut être formalisée via deux ensembles de base , l'ensemble des points et l'ensemble des lignes. De plus, une caractéristique frappante des plans projectifs est la symétrie des rôles joués par les points et les lignes . Un exemple moins géométrique : un graphe peut être formalisé via deux ensembles de base , l'ensemble des sommets (appelés aussi nœuds ou points) et l'ensemble des arêtes (appelés aussi arcs ou lignes). Généralement, un nombre fini d'ensembles de base principaux et un nombre fini d'ensembles de base auxiliaires sont stipulés par Bourbaki.

De nombreuses structures mathématiques de saveur géométrique traitées dans les sous-sections « Géométrie non commutative », « Schémas » et « Topoï » ci-dessus ne stipulent pas un ensemble de points de base. Par exemple, la « topologie inutile » (en d'autres termes, la topologie sans points ou la théorie des lieux) commence avec un seul ensemble de base dont les éléments imitent des ensembles ouverts dans un espace topologique (mais ne sont pas des ensembles de points) ; voir aussi meréotopologie et géométrie sans point .

Espaces mathématiques par nom

Voir également

• Structure mathématique
• Transport de structure
• Ensemble (mathématiques)

Remarques

Notes de bas de page

Les références

Cet article a été soumis à WikiJournal of Science pour une évaluation externe par des pairs universitaires en 2017 ( rapports des évaluateurs ). Le contenu mis à jour a été réintégré dans la page Wikipedia sous une licence CC-BY-SA-3.0 ( 2018 ). La version du dossier examinée est : Boris Tsirelson ; et al. (1er juin 2018). "Les espaces en mathématiques" (PDF) . WikiJournal des sciences . 1 (1) : 2. doi : 10.15347/WJS/2018.002 . ISSN  2470-6345 . Wikidata  Q55120290 .

• Bourbaki, Nicolas , Éléments de mathématiques , Hermann (original), Addison-Wesley (traduction).
• Bourbaki, Nicolas (1968), Éléments de mathématiques : Théorie des ensembles , Hermann (original), Addison-Wesley (traduction).
• Eisenbud, David ; Harris, Joe (2000), La géométrie des schémas , Springer-Verlag, doi : 10.1007/b97680 , ISBN 978-0-387-98638-8.
• Gowers, Timothée ; Barrow-Green, juin ; Chef, Imre , éd. (2008), The Princeton Companion to Mathematics , Princeton University Press, ISBN 978-0-691-11880-2.
• Itô, Kiyosi , éd. (1993), Dictionnaire encyclopédique des mathématiques (deuxième éd.), Société mathématique du Japon (original), MIT press (traduction).

Liens externes

• Médias liés à l' espace (mathématiques) sur Wikimedia Commons
• Matilde Marcolli (2009) La notion d'espace en mathématiques , de Caltech .