9 cubes - 9-cube

Enneract à 9 cubes
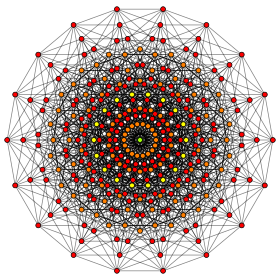Projection orthogonale à l' intérieur du polygone de Petrie Les sommets orange sont doublés, le jaune en a 4 et le centre vert en a 8
Type	Régulier 9-polytope
Famille	hypercube
Symbole Schläfli	{4,3 7 }
Diagramme de Coxeter-Dynkin
8 faces	18 {4,3 6 }
7 faces	144 {4,3 5 }
6 faces	672 {4,3 4 }
5 faces	2016 {4,3 3 }
4 faces	4032 {4,3,3}
Cellules	5376 {4,3}
Visages	4608 {4}
Bords	2304
Sommets	512
Figure de sommet	8 simplex
Polygone de Petrie	octadécagone
Groupe Coxeter	C 9 , [3 7 , 4]
Double	9-orthoplex
Propriétés	convexe

En géométrie , un 9-cube est un hypercube à neuf dimensions avec 512 sommets , 2304 arêtes , 4608 faces carrées , 5376 cellules cubiques , 4032 tesseract 4 faces , 2016 5-cube 5 faces , 672 6-cube 6 faces , 144 7 cubes 7 faces et 18 8 cubes 8 faces .

Il peut être nommé par son symbole Schläfli {4,3 ⁷ }, étant composé de trois 8 cubes autour de chaque 7 faces. Il est également appelé un enneract , un portemanteau de tesseract (le 4-cube ) et enne pour neuf (dimensions) en grec . Il peut également être appelé un octadéca-9-tope ou octadécayoton , comme un polytope à neuf dimensions construit avec 18 facettes régulières .

Il fait partie d'une famille infinie de polytopes, appelés hypercubes. Le dual d'un 9-cube peut être appelé 9-orthoplex et fait partie de la famille infinie des cross-polytopes .

Coordonnées cartésiennes

Les coordonnées cartésiennes des sommets d'un cube 9 centré à l'origine et la longueur d'arête 2 sont

(± 1, ± 1, ± 1, ± 1, ± 1, ± 1, ± 1, ± 1, ± 1)

tandis que l'intérieur du même se compose de tous les points ( x ₀ , x ₁ , x ₂ , x ₃ , x ₄ , x ₅ , x ₆ , x ₇ , x ₈ ) avec −1 <  x _i  <1.

Les projections

Ce graphe à 9 cubes est une projection orthogonale . Cette orientation montre les colonnes de sommets positionnées à une distance sommet-bord-sommet d'un sommet à gauche à un sommet à droite, et les arêtes attachant des colonnes adjacentes de sommets. Le nombre de sommets dans chaque colonne représente les lignes du triangle de Pascal , soit 1: 9: 36: 84: 126: 126: 84: 36: 9: 1.

Images

projections orthographiques

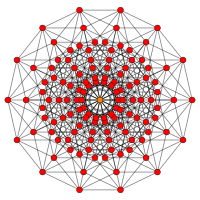
B 9		B 8		B 7
[18]		[16]		[14]
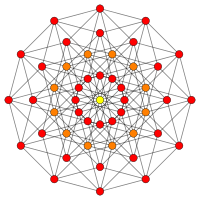
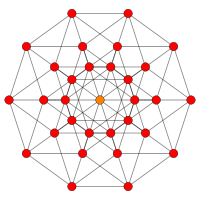
B 6			B 5
[12]			[dix]
B 4		B 3		B 2
[8]		[6]		[4]
A 7		A 5		A 3
[8]		[6]		[4]

Polytopes dérivés

L'application d'une opération d' alternance , la suppression de sommets alternés du 9-cube , crée un autre polytope uniforme , appelé 9-demicube , (partie d'une famille infinie appelée demihypercubes ), qui a 18 8-demicube et 256 8-simplex facettes.

Remarques

Références

• HSM Coxeter :
  • Coxeter, Regular Polytopes , (3e édition, 1973), édition Dover, ISBN   0-486-61480-8 , p. 296, Tableau I (iii): Polytopes réguliers, trois polytopes réguliers en n dimensions (n≥5)
  • HSM Coxeter, Regular Polytopes , 3e édition, Dover New York, 1973, p. 296, Tableau I (iii): Polytopes réguliers, trois polytopes réguliers en n dimensions (n≥5)
  • Kaleidoscopes: Selected Writings of HSM Coxeter , édité par F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN   978-0-471-01003-6 [1]
    • (Papier 22) HSM Coxeter, Polytopes réguliers et semi-réguliers I , [Math. Zeit. 46 (1940) 380-407, MR 2,10]
    • (Papier 23) HSM Coxeter, Polytopes réguliers et semi-réguliers II , [Math. Zeit. 188 (1985) 559-591]
    • (Papier 24) HSM Coxeter, Polytopes réguliers et semi-réguliers III , [Math. Zeit. 200 (1988) 3-45]
• Norman Johnson Uniform Polytopes , Manuscrit (1991)
  • NW Johnson: The Theory of Uniform Polytopes and Honeycombs , Ph.D. (1966)
• Klitzing, Richard. "Polytopes uniformes 9D (polyyotta) o3o3o3o3o3o3o3o4x - enne" .

Liens externes

• Weisstein, Eric W. "Hypercube" . MathWorld .
• Olshevsky, George. "Mesurer le polytope" . Glossaire de l'hyperespace . Archivé de l'original le 4 février 2007.
• Glossaire multidimensionnel: hypercube Garrett Jones