5-simplex - 5-simplex

Hexateron 5 simplex (hix)
Type	5-polytope uniforme
Symbole Schläfli	{3 4 }
Diagramme de Coxeter
4 faces	6	6 {3,3,3}
Cellules	15	15 {3,3}
Visages	20	20 {3}
Bords	15
Sommets	6
Figure de sommet	5 cellules
Groupe Coxeter	A 5 , [3 4 ], commande 720
Double	auto-double
Point de base	(0,0,0,0,0,1)
Circumradius	0,645497
Propriétés	convexe , isogonal régulier , auto-dual

En géométrie à cinq dimensions , un 5- simplex est un 5-polytope régulier auto-double . Il a six sommets , 15 arêtes , 20 faces triangulaires , 15 cellules tétraédriques et 6 facettes à 5 cellules . Il a un angle dièdre de cos ⁻¹ ( 1/5), soit environ 78,46 °.

Le 5-simplex est une solution au problème: faites 20 triangles équilatéraux en utilisant 15 allumettes, où chaque côté de chaque triangle est exactement une allumette.

Noms alternatifs

Il peut également être appelé un hexateron , ou hexa-5-tope , en tant que polytope à 6 facettes en 5 dimensions. Le nom hexatéron est dérivé de hexa- pour avoir six facettes et teron (avec ter- étant une corruption de tétra- ) pour avoir des facettes à quatre dimensions.

Par Jonathan Bowers, un hexatéron reçoit l'acronyme hix .

En tant que configuration

Cette matrice de configuration représente le 5-simplex. Les lignes et colonnes correspondent aux sommets, arêtes, faces, cellules et 4 faces. Les nombres diagonaux indiquent combien de chaque élément se produit dans tout le 5-simplex. Les nombres non diagonaux indiquent combien d'éléments de la colonne se trouvent dans ou à l'élément de la ligne. La matrice de cet auto-double simplex est identique à sa rotation de 180 degrés.

${\ displaystyle {\ begin {bmatrix} {\ begin {matrix} 6 & 5 & 10 & 10 & 5 \\ 2 & 15 & 4 & 6 & 4 \\ 3 & 3 & 20 & 3 & 3 \\ 4 & 6 & 4 & 15 & 2 \\ 5 & 10 & 10 & 5 & 6 \ end {matrix}} \ end {bmatrix}}}$

Coordonnées cartésiennes hexatéroniques régulières

L' hexatéron peut être construit à partir d'une 5 cellules en ajoutant un 6ème sommet de sorte qu'il soit équidistant de tous les autres sommets de la 5 cellule.

Les coordonnées cartésiennes des sommets d'un hexatéron régulier centré sur l'origine ayant une longueur d'arête 2 sont:

${\ displaystyle {\ begin {aligné} & \ left ({\ tfrac {1} {\ sqrt {15}}}, \ {\ tfrac {1} {\ sqrt {10}}}, \ {\ tfrac {1 } {\ sqrt {6}}}, \ {\ tfrac {1} {\ sqrt {3}}}, \ \ pm 1 \ right) \\ [5pt] & \ left ({\ tfrac {1} {\ sqrt {15}}}, \ {\ tfrac {1} {\ sqrt {10}}}, \ {\ tfrac {1} {\ sqrt {6}}}, \ - {\ tfrac {2} {\ sqrt {3}}}, \ 0 \ right) \\ [5pt] & \ left ({\ tfrac {1} {\ sqrt {15}}}, \ {\ tfrac {1} {\ sqrt {10}}} , \ - {\ tfrac {\ sqrt {3}} {\ sqrt {2}}}, \ 0, \ 0 \ right) \\ [5pt] & \ left ({\ tfrac {1} {\ sqrt {15 }}}, \ - {\ tfrac {2 {\ sqrt {2}}} {\ sqrt {5}}}, \ 0, \ 0, \ 0 \ right) \\ [5pt] & \ left (- { \ tfrac {\ sqrt {5}} {\ sqrt {3}}}, \ 0, \ 0, \ 0, \ 0 \ right) \ end {Aligné}}}$

Les sommets du 5-simplex peuvent être plus simplement positionnés sur un hyperplan dans le 6-espace comme des permutations de (0,0,0,0,0,1) ou (0,1,1,1,1,1). Ces constructions peuvent être vues comme des facettes du 6-orthoplex ou du 6-cube rectifié respectivement.

Images projetées

projections orthographiques

Un avion k Coxeter	A 5	A 4
Graphique
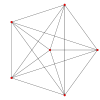
Symétrie dièdre	[6]	[5]
Un avion k Coxeter	A 3	A 2
Graphique
Symétrie dièdre	[4]	[3]

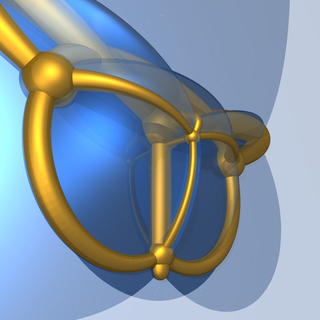Projection stéréographique 4D à 3D du diagramme de Schlegel 5D à 4D de l'hexatéron.

Formes de symétrie inférieure

Une forme de symétrie inférieure est une pyramide à 5 cellules () v {3,3,3}, avec un ordre de symétrie [3,3,3] 120, construite comme une base à 5 cellules dans un hyperplan à 4 espaces , et un sommet point au - dessus de l'hyperplan. Les cinq côtés de la pyramide sont constitués de cellules à 5 cellules. Ceux-ci sont vus comme des figures de sommet de 6-polytopes réguliers tronqués , comme un 6-cube tronqué .

Une autre forme est {} v {3,3}, avec [2,3,3] ordre de symétrie 48, la jonction d'un digon orthogonal et d'un tétraèdre, décalé orthogonalement, avec toutes les paires de sommets connectées entre elles. Une autre forme est {3} v {3}, avec [3,2,3] ordre de symétrie 36, et symétrie étendue [[3,2,3]], ordre 72. Elle représente la jonction de 2 triangles orthogonaux, décalés orthogonalement, avec toutes les paires de sommets connectés entre eux.

Celles-ci sont visibles sur les figures de sommets de 6-polytopes réguliers tronqués et tronqués, comme un 6-cube tronqué et un 6-simplex tronqué . Les étiquettes d'arête ici représentent les types de face le long de cette direction et représentent donc différentes longueurs d'arête.

Vertex chiffres pour les 6 simplex tronqués

() v {3,3,3}		{} v {3,3}		{3} v {3}
6 simplex tronqué	6 cubes tronqués	bitruncated 6-simplex	bitruncated 6 cubes	6 simplex tronqué

Composé

Le composé de deux 5-simplexes dans des configurations doubles peut être vu dans cette projection de plan A6 Coxeter , avec des sommets et des arêtes 5-simplex rouge et bleu. Ce composé a une symétrie [[3,3,3,3]], d'ordre 1440. L'intersection de ces deux 5-simplexes est un 5-simplex birectifié uniforme . = ∩ .

5-polytopes uniformes associés

Il s'agit du premier d'une série dimensionnelle de polytopes et de nids d'abeilles uniformes, exprimés par Coxeter sous la forme d'une série 1 _3k . Un cas à 4 dimensions dégénéré existe sous forme de pavage à 3 sphères, un dièdre tétraédrique .

1 figurines dimensionnelles _3k

Espace	Fini				Euclidienne	Hyperbolique
n	4	5	6	sept	8	9
Groupe Coxeter	A 3 A 1	A 5	D 6	E 7	${\ displaystyle {\ tilde {E}} _ {7}}$= E 7 +	${\ displaystyle {\ bar {T}} _ {8}}$= E 7 ++
Diagramme de Coxeter
Symétrie	[3 -1,3,1 ]	[3 0,3,1 ]	[3 1,3,1 ]	[3 2,3,1 ]	[[3 3,3,1 ]]	[3 4,3,1 ]
Ordre	48	720	23 040	2 903 040	∞
Graphique					-	-
Nom	1 3, -1	1 30	1 31	1 32	1 33	1 34

Il s'agit du premier d'une série dimensionnelle de polytopes et de nids d'abeilles uniformes, exprimés par Coxeter sous la forme d'une série 3 _k1 . Un cas dégénéré en 4 dimensions existe sous forme de pavage à 3 sphères, un hosohèdre tétraédrique .

3 chiffres dimensionnels _k1

Espace	Fini				Euclidienne	Hyperbolique
n	4	5	6	sept	8	9
Groupe Coxeter	A 3 A 1	A 5	D 6	E 7	${\ displaystyle {\ tilde {E}} _ {7}}$= E 7 +	${\ displaystyle {\ bar {T}} _ {8}}$= E 7 ++
Diagramme de Coxeter
Symétrie	[3 -1,3,1 ]	[3 0,3,1 ]	[[3 1,3,1 ]] = [4,3,3,3,3]	[3 2,3,1 ]	[3 3,3,1 ]	[3 4,3,1 ]
Ordre	48	720	46 080	2 903 040	∞
Graphique					-	-
Nom	3 1, -1	3 10	3 11	3 21	3 31	3 41

Le 5-simplex, comme 2 ₂₀ polytope est le premier d'une série dimensionnelle 2 _2k .

2 figures _2k de n dimensions

Espace	Fini			Euclidienne	Hyperbolique
n	4	5	6	sept	8
Groupe Coxeter	A 2 A 2	A 5	E 6	${\ displaystyle {\ tilde {E}} _ {6}}$= E 6 +	E 6 ++
Diagramme de Coxeter
Graphique				∞	∞
Nom	2 2, -1	2 20	2 21	2 22	2 23

Le 5-simplex régulier est l'un des 19 polytera uniformes basés sur le groupe [3,3,3,3] Coxeter , tous représentés ici dans les projections orthographiques du plan A ₅ Coxeter . (Les sommets sont colorés par ordre de chevauchement de projection, rouge, orange, jaune, vert, cyan, bleu, violet ayant progressivement plus de sommets)

Polytopes A5
t 0	t 1	t 2	t 0,1	t 0,2	t 1,2	t 0,3
t 1,3	t 0,4	t 0,1,2	t 0,1,3	t 0,2,3	t 1,2,3	t 0,1,4
t 0,2,4	t 0,1,2,3	t 0,1,2,4	t 0,1,3,4	t 0,1,2,3,4

Remarques

Références

• Gosset, T. (1900). "Sur les figures régulières et semi-régulières dans l'espace de n dimensions". Messager des mathématiques . Macmillan. pp. 43–.
• Coxeter, HSM :
  • - (1973). "Tableau I (iii): Polytopes réguliers, trois polytopes réguliers en n-dimensions (n≥5)". Regular Polytopes (3e éd.). Douvres. pp.  296 . ISBN 0-486-61480-8.
  • Sherk, F. Arthur; McMullen, Peter; Thompson, Anthony C .; Weiss, Asia Ivic, éds. (1995). Kaléidoscopes: Écrits sélectionnés du HSM Coxeter . Wiley. ISBN 978-0-471-01003-6.
    • (Papier 22) - (1940). "Polytopes réguliers et semi-réguliers I" . Math. Zeit . 46 : 380–407. doi : 10.1007 / BF01181449 . S2CID  186237114 .
    • (Papier 23) - (1985). "Polytopes II régulier et semi-régulier" . Math. Zeit . 188 (4): 559-591. doi : 10.1007 / BF01161657 . S2CID  120429557 .
    • (Papier 24) - (1988). "Polytopes III Régulier et Semi-Régulier" . Math. Zeit . 200 : 3–45. doi : 10.1007 / BF01161745 . S2CID  186237142 .
• Conway, John H .; Burgiel, Heidi; Goodman-Strass, Chaim (2008). "26. Hémicubes: 1 _n1 ". Les symétries des choses . p. 409. ISBN 978-1-56881-220-5.
• Johnson, Norman (1991). "Polytopes uniformes" (manuscrit). Citer le journal nécessite |journal=( aide )
  • Johnson, NW (1966). La théorie des polytopes uniformes et des nids d'abeilles (PhD). Université de Toronto.

Liens externes

• Olshevsky, George. "Simplex" . Glossaire de l'hyperespace . Archivé de l'original le 4 février 2007.
• Polytopes de différentes dimensions , Jonathan Bowers
• Glossaire multidimensionnel