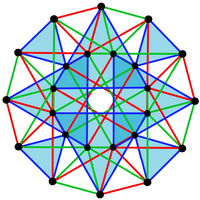
24 cellules - 24-cell
| 24 cellules | |
|---|---|

Diagramme de Schlegel
(sommets et arêtes) | |
| Taper | Convexe régulier 4-polytope |
| Symbole Schläfli | {3,4,3} r{3,3,4} = {3 1,1,1 } = |
| Diagramme de Coxeter |
|
| Cellules | 24 {3,4} |
| Visages | 96 {3} |
| Bords | 96 |
| Sommets | 24 |
| Figure de sommet | cube |
| Polygone de Pétrie | dodécagone |
| Groupe Coxeter | F 4 , [3,4,3], ordre 1152 B 4 , [4,3,3], ordre 384 D 4 , [3 1,1,1 ], ordre 192 |
| Double | Auto-dual |
| Propriétés | convexe , isogonal , isotoxal , isoedrique |
| Indice uniforme | 22 |
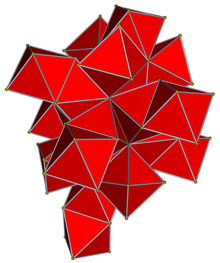
En géométrie , la cellule 24 est le 4-polytope régulier convexe (analogue à quatre dimensions d'un solide platonicien) avec le symbole de Schläfli {3,4,3}. Il est aussi appelé C 24 , ou le icositetrachoron , OCTAPLEX (abréviation de "complexe octaédrique"), icosatetrahedroid , octacube , hyper-diamant ou polyoctahedron , étant construit de octaédriques cellules .
La limite des 24 cellules est composée de 24 cellules octaédriques dont six se rencontrent à chaque sommet et trois à chaque bord. Ensemble, ils ont 96 faces triangulaires, 96 arêtes et 24 sommets. La figure du sommet est un cube . Le 24 cellules est auto-dual . Lui et le tesseract sont les seuls 4-polytopes réguliers convexes dans lesquels la longueur du bord est égale au rayon.
Le 24 cellules n'a pas d'analogue régulier en 3 dimensions. C'est le seul des six polytopes réguliers convexes qui n'est pas l'analogue à quatre dimensions de l'un des cinq solides platoniciens réguliers . Cependant, il peut être vu comme l'analogue d'une paire de solides irréguliers : le cuboctaèdre et son dual le dodécaèdre rhombique .
Les copies traduites des 24 cellules peuvent carreler l'espace à quatre dimensions face à face, formant le nid d'abeilles à 24 cellules . En tant que polytope pouvant carreler par translation, le 24-cell est un exemple de parallélotope , le plus simple qui n'est pas aussi un zonotope .
Géométrie
La cellule 24 incorpore les géométries de chaque polytope régulier convexe dans les quatre premières dimensions, à l'exception de la cellule 5, celles avec un 5 dans leur symbole Schlӓfli et les polygones {7} et au-dessus. Il est particulièrement utile d'explorer les 24 cellules, car on peut voir les relations géométriques entre tous ces polytopes réguliers dans un seul 24 cellules ou son nid d'abeilles .
Le 24-cellule est le quatrième dans la séquence de 6 4-polytopes réguliers convexes (par ordre de taille et de complexité). Il peut être déconstruit en 3 instances qui se chevauchent de son prédécesseur le tesseract (8 cellules), comme le 8 cellules peut être déconstruit en 2 instances qui se chevauchent de son prédécesseur le 16 cellules . La procédure inverse pour construire chacun de ceux-ci à partir d'une instance de son prédécesseur préserve le rayon du prédécesseur, mais produit généralement un successeur avec une longueur d'arête plus petite.
| 4-polytopes convexes réguliers | |||||||
|---|---|---|---|---|---|---|---|
| Groupe Symétrie | Un 4 | B 4 | F 4 | H 4 | |||
| Nom |
5 cellules hyper- |
16 cellules Hyper- |
8 cellules Hyper- |
24 cellules |
600 cellules Hyper- |
120 cellules Hyper- |
|
| Symbole Schläfli | {3, 3, 3} | {3, 3, 4} | {4, 3, 3} | {3, 4, 3} | {3, 3, 5} | {5, 3, 3} | |
| Diagramme de Coxeter |
|
|
|
|
|
|
|
| Graphique |

|

|

|

|

|

|
|
| Sommets | 5 | 8 | 16 | 24 | 120 | 600 | |
| Bords | dix | 24 | 32 | 96 | 720 | 1200 | |
| Visages | 10 triangles |
32 triangles |
24 carrés |
96 triangles |
1200 triangles |
720 pentagones |
|
| Cellules | 5 tétraèdres |
16 tétraèdres |
8 cubes |
24 octaèdres |
600 tétraèdres |
120 dodécaèdres |
|
| Rayon long | 1 | 1 | 1 | 1 | 1 | 1 | |
| Longueur du bord | √ 5/√ 2 1.581 | √ 2 ≈ 1,414 | 1 | 1 | 1/?? 0,618 | 1/√ 2 φ 2 0,270 | |
| Rayon court | 1/4 | 1/2 | 1/2 | √ 2/2 0,707 | 1 - (√ 2/2 √ 3 φ) 2 0,936 | 1 - (1/2 √ 3 φ) 2 0,968 | |
| Zone | dix•√ 8/3 9.428 | 32•√ 3/4 13.856 | 24 | 96•√ 3/4 41.569 | 1200•√ 3/8φ 2 99.238 | 720•25 + 10 √ 5/8φ 4 621,9 | |
| Le volume | 5•5 √ 5/24 2.329 | 16•1/3 5.333 | 8 | 24•√ 2/3 11.314 | 600•1/3 √ 8 φ 3 16.693 | 120•2 + φ/2 √ 8 φ 3 18.118 | |
| 4-Contenu | √ 5/24•(√ 5/2) 4 0,146 | 2/3 0,667 | 1 | 2 | Court∙Vol/4 3.907 | Court∙Vol/4 4.385 | |
Coordonnées
Carrés
La cellule 24 est l' enveloppe convexe de ses sommets qui peuvent être décrits comme les 24 permutations de coordonnées de :
- .
Ces coordonnées peuvent être construites comme ![]()
![]()
![]()
![]()
![]()
![]()
![]() , rectifiant le 16-cell
, rectifiant le 16-cell ![]()
![]()
![]()
![]()
![]()
![]()
![]() avec 8 permutations de sommets de (±2,0,0,0). La figure de sommet d'une cellule à 16 est l' octaèdre ; ainsi, couper les sommets de la cellule 16 au milieu de ses bords incidents produit 8 cellules octaédriques. Ce processus rectifie également les cellules tétraédriques des 16 cellules qui deviennent 16 octaèdres, donnant aux 24 cellules 24 cellules octaédriques.
avec 8 permutations de sommets de (±2,0,0,0). La figure de sommet d'une cellule à 16 est l' octaèdre ; ainsi, couper les sommets de la cellule 16 au milieu de ses bords incidents produit 8 cellules octaédriques. Ce processus rectifie également les cellules tétraédriques des 16 cellules qui deviennent 16 octaèdres, donnant aux 24 cellules 24 cellules octaédriques.
Dans ce référentiel, les 24 cellules ont des arêtes de longueur √ 2 et sont inscrites dans une 3-sphère de rayon √ 2 . Remarquablement, la longueur du bord est égale au cercle circonscrit, comme dans l' hexagone ou le cuboctaèdre . De tels polytopes sont radialement équilatéraux .
Les 24 sommets forment 18 grands carrés (3 ensembles de 6 carrés centraux orthogonaux), dont 3 se coupent à chaque sommet. En ne visualisant qu'un carré à chaque sommet, les 24 cellules peuvent être vues comme les sommets de 3 paires de grands carrés complètement orthogonaux qui ne se coupent à aucun sommet.
Hexagones
La cellule 24 est auto-duale , ayant le même nombre de sommets (24) que les cellules et le même nombre d'arêtes (96) que les faces.
Si le dual des 24 cellules ci-dessus de longueur d'arête √ 2 est obtenu en l'alternant autour de sa sphère inscrite , une autre cellule de 24 est trouvée qui a une longueur d'arête et un rayon de circonférence 1, et ses coordonnées révèlent plus de structure. Dans ce référentiel, les 24 cellules se trouvent au sommet, et ses sommets peuvent être donnés comme suit :
8 sommets obtenus en permutant les coordonnées entières :
- (±1, 0, 0, 0)
et 16 sommets de coordonnées demi-entières de la forme :
- (±1/2, ±1/2, ±1/2, ±1/2)
dont les 24 se trouvent à la distance 1 de l'origine.
Considérés comme des quaternions , ce sont les quaternions unitaires de Hurwitz .
Les 24 cellules ont un rayon unitaire et une longueur d'arête unitaire dans ce système de coordonnées. Nous appelons le système coordonnées de rayon unitaire pour le distinguer des autres, comme les coordonnées de rayon √ 2 utilisées ci-dessus .
Les 24 sommets et 96 arêtes forment 16 grands hexagones non orthogonaux, dont quatre se coupent à chaque sommet. En ne visualisant qu'un seul hexagone à chaque sommet, les 24 cellules peuvent être vues comme les 24 sommets de 4 grands cercles hexagonaux non sécants qui sont parallèles à Clifford .
Les 12 axes et 16 hexagones des 24 cellules constituent une configuration de Reye , qui dans le langage des configurations s'écrit 12 4 16 3 pour indiquer que chaque axe appartient à 4 hexagones, et chaque hexagone contient 3 axes.
Triangles
Les 24 sommets forment 32 grands triangles équilatéraux inscrits dans les 16 grands hexagones.
Accords hypercubiques
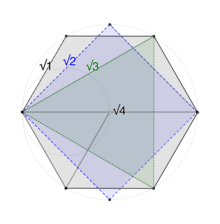
Les 24 sommets de la répartition 24 des cellules à quatre différents accords longueurs les unes des autres: √ 1 , √ 2 , √ 3 et √ 4 .
Chaque sommet est joint à 8 autres par une arête de longueur 1, s'étendant sur 60° = ??/3d'arc. Les prochains sommets les plus proches sont 6 sommets situés à 90° =??/2loin, le long d'une corde intérieure de longueur √ 2 . 8 autres sommets se trouvent à 120° =2 π/3loin, le long d'une corde intérieure de longueur √ 3 . Le sommet opposé est éloigné de 180° = π le long d'un diamètre de longueur 2. Enfin, comme la cellule 24 est radialement équilatérale, son centre peut être traité comme un sommet canonique du 25e sommet, qui est à 1 longueur d'arête de tous les autres.
Pour visualiser la façon dont les polytopes intérieures de la forme de 24 cellules en même temps (comme décrit ci - dessous ), garder à l' esprit que les quatre longueurs de corde ( √ 1 , √ 2 , √ 3 , √ 4 ) sont les longs diamètres des hypercubes de dimensions 1 à 4 : le grand diamètre du carré est √ 2 ; le grand diamètre du cube est √ 3 ; et le grand diamètre du tesseract est √ 4 . De plus, le grand diamètre de l'octaèdre est √ 2 comme le carré; et le long diamètre des 24 cellules elle-même est √ 4 comme le tesseract. Dans la 24 cellule, les √ 2 cordes sont les bords des carrés centraux et les √ 4 accords sont les diagonales des carrés centraux.
Géodésiques

Les cordes des sommets des 24 cellules sont disposées en polygones de grand cercle géodésique . La distance géodésique entre deux sommets 24 des cellules le long d' un trajet de √ 1 bords est toujours 1, 2, ou 3, et il est 3 uniquement pour les sommets opposés.
Les √ 1 bords se produisent dans 16 grands cercles hexagonaux (dans des plans inclinés à 60 degrés les uns des autres), 4 qui se croisent à chaque sommet. Les 96 arêtes distinctes √ 1 divisent la surface en 96 faces triangulaires et 24 cellules octaédriques : une à 24 cellules. Les 16 grands cercles hexagonaux peuvent être divisés en 4 ensembles de 4 géodésiques parallèles Clifford sans intersection , de sorte qu'un seul grand cercle hexagonal de chaque ensemble passe par chaque sommet et que les 4 hexagones de chaque ensemble atteignent les 24 sommets.
Les √ 2 cordes se produisent dans 18 grands cercles carrés (3 séries de 6 plans orthogonaux), 3 qui se croisent à chaque sommet. Les 72 cordes √ 2 distinctes ne s'étendent pas dans les mêmes plans que les grands cercles hexagonaux ; ils ne suivent pas les bords des 24 cellules, ils passent par ses centres de cellules octogonaux. Les 18 grands cercles carrés peuvent être divisés en 3 ensembles de 6 géodésiques parallèles Clifford sans intersection, de sorte qu'un seul grand cercle carré de chaque ensemble passe par chaque sommet et que les 6 carrés de chaque ensemble atteignent les 24 sommets.
Les √ 3 accords se produisent dans 32 cercles triangulaires grands dans 16 plans, dont 4 se croisent à chaque sommet. Les 96 distincts √ 3 cordes entrent sommet à chaque sommet-autre-dans les mêmes plans que les cercles hexagonaux grands.
Les cordes √ 4 se présentent sous la forme de 12 diamètres sommet à sommet (3 ensembles de 4 axes orthogonaux), les 24 rayons autour du 25e sommet central.
La somme des longueurs au carré de tous ces accords distincts des 24 cellules est 576 = 24 2 . Ce sont tous les polygones centraux passant par les sommets, mais dans l'espace 4, il y a des géodésiques sur la sphère 3 qui ne se trouvent pas du tout dans des plans centraux. Il existe des chemins géodésiques les plus courts entre deux sommets à 24 cellules qui sont hélicoïdaux plutôt que simplement circulaires ; elles correspondent à des rotations isocliniques diagonales plutôt qu'à de simples rotations.
Les √ 1 bords se produisent dans 48 paires parallèles, √ 3 part. Les √ 2 cordes se produisent dans 36 paires parallèles, √ 2 morceaux. Les √ 3 accords se produisent dans 48 paires parallèles, √ une de l' autre.
Les plans centraux des 24 cellules peuvent être divisés en 4 hyperplans centraux (3 espaces) formant chacun un cuboctaèdre . Les grands carrés sont distants de 90 degrés ; les grands hexagones sont distants de 60 degrés ; un grand carré et un grand hexagone sont distants de 60 degrés. Chaque ensemble de polygones centraux similaires (carrés ou hexagones) peut être divisé en 4 ensembles de polygones parallèles Clifford non sécants (de 6 carrés ou 4 hexagones). Chaque ensemble de grands cercles parallèles de Clifford est un faisceau de fibres parallèles qui visite les 24 sommets une seule fois.
Chaque grand cercle croise les autres grands cercles auxquels il n'est pas parallèle à Clifford à un diamètre √ 4 des 24 cellules. Les grands cercles complètement orthogonaux ou parallèles à Clifford ne se coupent pas du tout : ils passent par des ensembles disjoints de sommets.
Bâtiments
Les triangles et les carrés se réunissent uniquement dans les 24 cellules pour générer, en tant qu'éléments intérieurs, tous les polytopes convexes réguliers à faces triangulaires et carrées dans les quatre premières dimensions (avec des mises en garde pour les cellules à 5 et 600 cellules ) . Par conséquent, il existe de nombreuses façons de construire ou de déconstruire les 24 cellules.
Constructions réciproques de 8 cellules et 16 cellules
Les 8 sommets entiers (±1, 0, 0, 0) sont les sommets d'une cellule régulière de 16 , et les 16 sommets demi-entiers (±1/2, ±1/2, ±1/2, ±1/2) sont les sommets de son dual, le tesseract (8-cellule). Le tesseract donne la construction de Gosset du 24 cellules, équivalent à couper un tesseract en 8 pyramides cubiques , puis à les attacher aux facettes d'un deuxième tesseract. La construction analogue en 3-espace donne le dodécaèdre rhombique qui, cependant, n'est pas régulier. Le 16-cell donne la construction réciproque du 24-cell, la construction de Cesaro, équivalent à rectifier un 16-cell (tronquer ses coins au milieu des bords, comme décrit ci - dessus ). La construction analogue en 3-espace donne le cuboctaèdre (dual du dodécaèdre rhombique) qui, cependant, n'est pas régulier. Le tesseract et le 16-cell sont les seuls 4-polytopes réguliers dans le 24-cell.
On peut encore diviser les 16 sommets demi-entiers en deux groupes : ceux dont les coordonnées contiennent un nombre pair de signes moins (−) et ceux dont les coordonnées contiennent un nombre impair. Chacun de ces groupes de 8 sommets définit également une cellule régulière de 16. Cela montre que les sommets des 24 cellules peuvent être regroupés en trois ensembles disjoints de huit, chaque ensemble définissant une cellule régulière de 16 et le complément définissant le double tesseract. Cela montre également que les symétries de la cellule 16 forment un sous-groupe d'indice 3 du groupe de symétrie de la cellule 24.
Diminutions
Nous pouvons facetter les 24 cellules en coupant à travers les cellules intérieures délimitées par des cordes de sommets pour supprimer les sommets, exposant les facettes des 4-polytopes intérieurs inscrits dans les 24 cellules. On peut couper une cellule de 24 à travers n'importe quel hexagone planaire de 6 sommets, n'importe quel rectangle planaire de 4 sommets, ou n'importe quel triangle de 3 sommets. Les plans centraux du grand cercle ( ci-dessus ) ne sont que quelques-uns de ces plans. Ici, nous allons exposer quelques-uns des autres : les plans de face des polytopes intérieurs.
8 cellules
En partant d'un 24 cases complet, supprimer 8 sommets orthogonaux (4 paires opposées sur 4 axes perpendiculaires), et les 8 arêtes qui rayonnent de chacune, en coupant 8 cases cubiques délimitées par √ 1 arêtes pour supprimer 8 pyramides cubiques dont les sommets sont les sommets à supprimer. Cela supprime 4 arêtes de chaque grand cercle hexagonal (en conservant une seule paire d'arêtes opposées), de sorte qu'il ne reste aucun grand cercle hexagonal continu. Maintenant, 3 arêtes perpendiculaires se rencontrent et forment le coin d'un cube à chacun des 16 sommets restants, et les 32 arêtes restantes divisent la surface en 24 faces carrées et 8 cellules cubiques : un tesseract . Il y a trois façons de le faire (choisir un ensemble de 8 sommets orthogonaux sur 24), il y a donc trois tesseracts inscrits dans les 24 cellules. Ils se chevauchent, mais la plupart de leurs ensembles d'éléments sont disjoints : ils partagent un certain nombre de sommets, mais aucune longueur d'arête, surface de face ou volume de cellule. Ils partagent 4 contenus, leur noyau commun.
16 cellules
En partant d'un 24 cellules complètes, supprimez les 16 sommets d'un tesseract (en conservant les 8 sommets que vous avez supprimés ci-dessus), en coupant à travers 16 cellules tétraédriques délimitées par √ 2 cordes pour supprimer 16 pyramides tétraédriques dont les sommets sont les sommets à supprimer. Cela supprime 12 grandes places (conservant un seul ensemble orthogonal) et tous les √ 1 arêtes, exposant √ 2 accords que les nouveaux bords. Maintenant, les 6 grands carrés restants se croisent perpendiculairement, 3 à chacun des 8 sommets restants, et leurs 24 arêtes divisent la surface en 32 faces triangulaires et 16 cellules tétraédriques : une cellule de 16 . Il y a trois façons de le faire (supprimer 1 des 3 ensembles de sommets de tesseract), il y a donc trois de ces 16 cellules inscrites dans les 24 cellules. Ils se chevauchent, mais tous leurs ensembles d'éléments sont disjoints : ils ne partagent aucun nombre de sommets, longueur d'arête ou surface de face, mais ils partagent le volume des cellules. Ils partagent également 4-contenu, leur noyau commun.
Constructions tétraédriques
La 24 cellule peut être construite radialement à partir de 96 triangles équilatéraux de longueur d'arête √ 1 qui se rencontrent au centre du polytope, chacun contribuant deux rayons et un bord. Ils forment 96 √ 1 tétraèdres (chacun contribuant à une face de 24 cellules), partageant tous le 25e sommet central de l'apex. Ceux-ci forment 24 pyramides octaédriques (demi à 16 cellules) avec leurs sommets au centre.
La 24 cellule peut être construite à partir de 96 triangles équilatéraux de longueur d'arête √ 2 , où les trois sommets de chaque triangle sont situés à 90 ° =??/2Loin les uns des autres. Ils forment 48 tétraèdres √ 2 (les cellules des trois 16 cellules ), centrés aux 24 rayons médians des 24 cellules.
Relations entre les polytopes intérieurs
Les 24 cellules, les trois tesseracts et les trois 16 cellules sont profondément entrelacées autour de leur centre commun et se croisent dans un noyau commun. Les tesseracts sont inscrits dans les 24 cellules de telle sorte que leurs sommets et leurs arêtes sont des éléments extérieurs des 24 cellules, mais leurs faces carrées et cellules cubiques se trouvent à l'intérieur des 24 cellules (ce ne sont pas des éléments des 24 cellules). Les 16 cellules sont inscrites dans les 24 cellules de telle sorte que seuls leurs sommets sont des éléments extérieurs des 24 cellules : leurs arêtes, faces triangulaires et cellules tétraédriques se trouvent à l'intérieur des 24 cellules. Les bords 16 des cellules intérieures ont une longueur √ 2 .
Les cellules de 16 sont également inscrites dans les tesseracts: leurs √ 2 arêtes sont les diagonales de face du tesseract, et leurs 8 sommets occupent tous les autres sommets de la tesseract. Chaque tesseract a deux 16 cellules inscrites (occupant les sommets opposés et les diagonales des faces), donc chaque 16 cellules est inscrite dans deux des trois 8 cellules. Cela rappelle la façon dont, en 3 dimensions, deux tétraèdres peuvent s'inscrire dans un cube, comme l'a découvert Kepler. En fait, c'est l'analogie dimensionnelle exacte (les demihypercubes ), et les 48 cellules tétraédriques sont inscrites dans les 24 cellules cubiques de cette façon.
Les 24 cellules renferment les trois tesseracts dans son enveloppe de facettes octaédriques, laissant un espace à 4 dimensions à certains endroits entre son enveloppe et l'enveloppe de cubes de chaque tesseract. Chaque tesseract renferme deux des trois 16 cellules, laissant un espace à 4 dimensions à certains endroits entre son enveloppe et l'enveloppe de chaque tétraèdre à 16 cellules. Ainsi, il existe des interstices mesurables en 4 dimensions entre les enveloppes à 24, 8 et 16 cellules. Les formes remplissant ces vides sont les 4 pyramides , évoquées ci-dessus.
Cellules limites
Malgré les interstices en 4 dimensions entre les enveloppes à 24, 8 et 16 cellules, leurs volumes en 3 dimensions se chevauchent. Les différentes enveloppes sont séparées à certains endroits, et en contact à d'autres endroits (où aucune 4-pyramide ne se trouve entre elles). Là où elles sont en contact, elles fusionnent et partagent le volume cellulaire : ce sont la même membrane tridimensionnelle à ces endroits, pas deux couches tridimensionnelles distinctes mais adjacentes. Parce qu'il y a au total 7 enveloppes, il y a des endroits où plusieurs enveloppes se rejoignent et se confondent en volume, et aussi des endroits où les enveloppes s'interpénètrent (se croisent de l'intérieur vers l'extérieur les unes des autres).
Certaines caractéristiques intérieures se trouvent dans l'espace 3 de l'enveloppe limite (extérieure) des 24 cellules elle-même : chaque cellule octaédrique est coupée en deux par trois carrés perpendiculaires (un de chacun des tesseracts), et les diagonales de ces carrés (qui croisent perpendiculairement au centre de l'octaèdre) sont des bords de 16 cellules (un de chaque 16 cellules). Chaque carré divise un octaèdre en deux pyramides carrées et lie également deux cellules cubiques adjacentes d'un tesseract ensemble comme leur face commune.
Comme nous l' avons vu ci - dessus, 16 des cellules √ 2 cellules tétraédriques sont inscrites dans tesseract √ 1 cellules cubiques, partageant le même volume. 24 cellules √ 1 octaédriques chevauchent leur volume avec √ 1 cellules cubiques : elles sont coupées en deux par une face carrée en deux pyramides carrées, dont les sommets se trouvent également à un sommet d'un cube. Les octaèdres partagent le volume non seulement avec les cubes, mais avec les tétraèdres qui y sont inscrits ; ainsi, les 24 cellules, les tesseracts et les 16 cellules partagent tous un certain volume limite.
En tant que configuration
Cette matrice de configuration représente les 24 cellules. Les lignes et les colonnes correspondent aux sommets, aux arêtes, aux faces et aux cellules. Les nombres diagonaux indiquent combien de chaque élément se produit dans l'ensemble des 24 cellules. Les nombres non diagonaux indiquent combien d'éléments de la colonne se trouvent dans ou au niveau de l'élément de la ligne.
Étant donné que la cellule 24 est auto-duale, sa matrice est identique à sa rotation de 180 degrés.
Symétries, systèmes racinaires et pavages
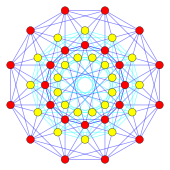
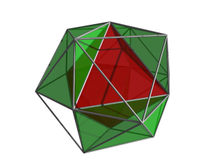
Les 24 vecteurs racines du système racinaire D 4 du groupe de Lie simple SO(8) forment les sommets d'une 24 cellules. Les sommets peuvent être vus dans 3 hyperplans , avec les 6 sommets d'une cellule d' octaèdre sur chacun des hyperplans extérieurs et 12 sommets d'un cuboctaèdre sur un hyperplan central. Ces sommets, combinés avec les 8 sommets de la cellule 16 , représentent les 32 vecteurs racines des groupes de Lie simples B 4 et C 4 .
Les 48 sommets (ou à proprement parler leurs rayons vecteurs) de l'union des 24 cellules et de son dual forment le système racinaire de type F 4 . Les 24 sommets des 24 cellules originales forment un système racinaire de type D 4 ; sa taille a le rapport √ 2 :1. Ceci est également vrai pour les 24 sommets de son dual. Le groupe de symétrie complet des 24 cellules est le groupe de Weyl de F 4 , qui est généré par des réflexions à travers les hyperplans orthogonaux aux racines de F 4 . Il s'agit d'un groupe résoluble d'ordre 1152. Le groupe de symétrie de rotation des 24 cellules est d'ordre 576.
Interprétation quaternionique

Lorsqu'il est interprété comme les quaternions , le réseau racine F 4 (qui est l'étendue intégrale des sommets des 24 cellules) est fermé par multiplication et est donc un anneau . C'est l'anneau des quaternions intégraux de Hurwitz . Les sommets des 24 cellules forment le groupe d'unités (c'est-à-dire le groupe d'éléments inversibles) dans l'anneau de quaternion de Hurwitz (ce groupe est également connu sous le nom de groupe tétraédrique binaire ). Les sommets des 24 cases sont précisément les 24 quaternions de Hurwitz de norme au carré 1, et les sommets des 24 cases duales sont ceux de norme au carré 2. Le réseau racine D 4 est le dual du F 4 et est donné par le sous-anneau des quaternions de Hurwitz de norme au carré pair.
Considérés comme les 24 quaternions d'Hurwitz , les coordonnées du rayon unitaire des 24 cellules représentent (en paires antipodales) les 12 rotations d'un tétraèdre régulier.
Les sommets d'autres 4-polytopes réguliers convexes forment également des groupes multiplicatifs de quaternions, mais peu d'entre eux génèrent un réseau racinaire.
Cellules de Voronoï
Les cellules de Voronoï du réseau racinaire D 4 sont des cellules régulières de 24. Le pavage de Voronoi correspondant donne le pavage de l' espace euclidien à 4 dimensions par 24 cellules régulières, le nid d'abeilles à 24 cellules . Les 24 cellules sont centrées aux points du réseau D 4 (quaternions de Hurwitz de norme paire au carré) tandis que les sommets sont aux points du réseau F 4 de norme au carré impair. Chaque 24 cellules de ce pavage a 24 voisins. Avec chacun d'eux, il partage un octaèdre. Il a également 24 autres voisins avec lesquels il ne partage qu'un seul sommet. Huit 24 cellules se rencontrent à un sommet donné de ce pavage. Le symbole Schläfli pour ce pavage est {3,4,3,3}. C'est l'une des trois seules tessellations régulières de R 4 .
Les boules unitaires inscrites dans les 24 alvéoles de ce pavage donnent lieu à l'empilement en treillis le plus dense connu d' hypersphères en 4 dimensions. Il a également été démontré que la configuration des sommets des 24 cellules donne le nombre de baisers le plus élevé possible en 4 dimensions .
Nid d'abeille radialement équilatéral
La double tessellation du nid d'abeilles à 24 cellules {3,4,3,3} est le nid d'abeilles à 16 cellules {3,3,4,3} . La troisième tessellation régulière de l'espace à quatre dimensions est le nid d'abeille tessératique {4,3,3,4} , dont les sommets peuvent être décrits par des coordonnées cartésiennes à 4 entiers. Les relations congruentes entre ces trois pavages peuvent être utiles pour visualiser les 24 cellules, en particulier la symétrie radiale équilatérale qu'elle partage avec le tesseract.
Un nid d'abeilles de longueur de bord unitaire 24 cellules peut être superposé sur un nid d'abeilles de tesseracts de longueur de bord unitaire de telle sorte que chaque sommet d'un tesseract (chaque coordonnée de 4 entiers) soit également le sommet d'un 24 cellules (et les bords du tesseract sont également de 24 cellules). -cell edge), et chaque centre d'une cellule à 24 est également le centre d'un tesseract. Les 24 cellules sont deux fois plus grandes que les tesseracts par leur contenu en 4 dimensions (hypervolume), donc globalement il y a deux tesseracts pour chaque 24 cellules, dont seulement la moitié sont inscrites dans une 24 cellules. Si ces tesseracts sont colorés en noir et que leurs tesseracts adjacents (avec lesquels ils partagent une facette cubique) sont colorés en rouge, un damier à 4 dimensions en résulte. Sur les 24 rayons centre-sommet de chaque 24 cellules, 16 sont également les rayons d'un tesseract noir inscrit dans les 24 cellules. Les 8 autres rayons s'étendent à l'extérieur du tesseract noir (à travers les centres de ses facettes cubiques) jusqu'aux centres des 8 tesseracts rouges adjacents. Ainsi, le nid d'abeilles à 24 cellules et le nid d'abeilles tessératique coïncident d'une manière particulière : 8 des 24 sommets de chaque 24 cellules ne se produisent pas à un sommet d'un tesseract (ils se produisent plutôt au centre d'un tesseract). Chaque tesseract noir est découpé dans un 24 cellules en le tronquant à ces 8 sommets, en coupant 8 pyramides cubiques (comme pour inverser la construction de Gosset, mais au lieu d'être retirées, les pyramides sont simplement colorées en rouge et laissées en place). Huit 24 cellules se rencontrent au centre de chaque tesseract rouge : chacune rencontre son opposé à ce sommet partagé, et les six autres à une cellule octaédrique partagée.
Les tesseracts rouges sont des cellules remplies (elles contiennent un sommet central et des rayons); les tesseracts noirs sont des cellules vides. L'ensemble de sommets de cette union de deux nids d'abeilles comprend les sommets de toutes les 24 cellules et tesseracts, ainsi que les centres des tesseracts rouges. L'ajout des centres de 24 cellules (qui sont également les centres de tesseract noirs) à ce nid d'abeilles donne un nid d'abeilles à 16 cellules, dont l'ensemble de sommets comprend tous les sommets et centres de tous les 24 cellules et tesseracts. Les centres autrefois vides des 24 cellules adjacentes deviennent les sommets opposés d'une longueur d'arête unitaire de 16 cellules. 24 demi-16 cellules (pyramides octaédriques) se rencontrent à chaque centre autrefois vide pour remplir chaque 24 cellules, et leurs bases octaédriques sont les facettes octaédriques à 6 sommets des 24 cellules (partagées avec les 24 cellules adjacentes).
Remarquez l'absence totale de pentagones n'importe où dans cette union de trois nids d'abeilles. Comme l'espace euclidien à 24 cellules, l'espace euclidien à 4 dimensions lui-même est entièrement rempli par un complexe de tous les polytopes qui peuvent être construits à partir de triangles et de carrés réguliers (à l'exception de la cellule à 5), mais ce complexe n'exige pas (ou ne permet pas) l'un des polytopes pentagonaux.
Rotations
Les 4-polytopes convexes réguliers sont une expression de leur symétrie sous-jacente qui est connue sous le nom de SO(4) , le groupe de rotations autour d'un point fixe dans l'espace euclidien à 4 dimensions.
Les 3 bases cartésiennes des 24 cellules
Il y a trois orientations distinctes du nid d'abeilles tessératique qui pourraient coïncider avec le nid d'abeilles à 24 alvéoles , selon lequel des trois ensembles disjoints des 24 alvéoles de 8 sommets orthogonaux (quel ensemble de 4 axes perpendiculaires, ou de manière équivalente, qui inscrit base 16-cell ) a été choisi pour l'aligner, tout comme trois tesseracts peuvent être inscrits dans les 24 cases, tournés les uns par rapport aux autres. La distance d'une de ces orientations à l'autre est une rotation isocline de 60 degrés (une double rotation de 60 degrés dans chaque paire de plans invariants orthogonaux, autour d'un seul point fixe). Cette rotation peut être vue plus clairement dans les plans centraux hexagonaux, où l'hexagone tourne pour changer lequel de ses trois diamètres est aligné avec un axe de système de coordonnées.
Plans de rotation
Les rotations dans l'espace euclidien à 4 dimensions peuvent être vues comme la composition de deux rotations à 2 dimensions dans des plans complètement orthogonaux. Ainsi la rotation générale dans l'espace 4 est une double rotation . Il existe deux cas particuliers importants, appelés rotation simple et rotation isocline .
Rotations simples

En 3 dimensions, un polyèdre en rotation a un seul plan de rotation central invariant . Le plan est dit invariant car chaque point du plan se déplace en cercle mais reste dans le plan. Un seul des plans centraux d'un polyèdre peut être invariant au cours d'une rotation particulière ; le choix du plan central invariant, et la distance angulaire sur laquelle il est tourné, spécifie complètement la rotation. Les points en dehors du plan invariant se déplacent également en cercles (sauf s'ils se trouvent sur l' axe de rotation fixe perpendiculaire au plan invariant), mais les cercles ne se trouvent pas dans un plan central .
Lorsqu'un 4-polytope tourne avec un seul plan central invariant, le même type de rotation simple se produit en 3 dimensions. La seule différence est qu'au lieu d'un axe de rotation fixe, il existe tout un plan central fixe dans lequel les points ne bougent pas. Le plan fixe est le seul plan central qui est complètement orthogonal au plan de rotation invariant. Dans la cellule 24, il y a une rotation simple qui amènera n'importe quel sommet directement à n'importe quel autre sommet, déplaçant également la plupart des autres sommets mais laissant au moins 2 et au plus 6 autres sommets fixes (les sommets que le plan central fixe coupe ). Le sommet se déplace le long d'un grand cercle dans le plan de rotation invariant entre les sommets adjacents d'un grand hexagone, d'un grand carré ou d'un grand digone , et le plan fixe complètement orthogonal est respectivement un digone, un carré ou un hexagone.
Double rotation

Les points dans le plan central complètement orthogonal ne sont pas contraints à être fixes. Il est également possible qu'ils tournent en cercles, en tant que deuxième plan invariant, à une vitesse indépendante de la rotation du premier plan invariant : une double rotation dans deux plans de rotation à la fois. Dans une double rotation, il n'y a pas de plan ou d'axe fixe : chaque point se déplace sauf le point central. La distance angulaire tournée peut être différente dans les deux plans centraux complètement orthogonaux, mais ils sont toujours tous les deux invariants : leurs points en mouvement circulaire restent dans le plan car tout le plan s'incline latéralement dans la rotation complètement orthogonale. Une rotation dans l'espace 4 a toujours (au moins) deux plans de rotation invariants complètement orthogonaux, bien que dans une rotation simple l'angle de rotation dans l'un d'eux soit 0.
Les doubles rotations se présentent sous deux formes chirales : les rotations gauche et droite . Dans une double rotation, chaque sommet se déplace en spirale le long de deux grands cercles complètement orthogonaux à la fois. Soit le chemin est fileté à droite (comme la plupart des vis et boulons), se déplaçant le long des cercles dans les "mêmes" directions, soit il est fileté à gauche (comme un boulon à filetage inversé), se déplaçant le long des cercles dans ce que nous disons conventionnellement sont des directions "opposées" (selon la règle de la main droite par laquelle nous disons conventionnellement quelle est la direction "vers le haut" sur chacun des 4 axes de coordonnées).
Rotations isocliniques
Lorsque les angles de rotation dans les deux plans invariants sont exactement les mêmes, une symétrie remarquable se produit : tous les grands plans circulaires Clifford parallèles aux plans invariants deviennent eux-mêmes des plans de rotation invariants, par ce même angle, et le 4-polytope tourne de manière isoclinique dans plusieurs directions à la fois. Chaque sommet se déplace d'une distance égale dans les quatre dimensions en même temps. Dans les 24 cellules, toute rotation isocline de 60 degrés dans un plan hexagonal amène chaque sommet à un sommet voisin, fait pivoter les 16 hexagones de 60 degrés et prend chaque polygone de grand cercle (carré, hexagone ou triangle) à un grand cercle parallèle à Clifford polygone du même genre à 60 degrés. Une rotation isocline est aussi appelée un déplacement de Clifford , d'après son découvreur .
Les 24 cellules de l' animation à double rotation semblent se retourner. Il semble, parce qu'il le fait, d'inverser la chiralité de l'ensemble des 4 polytopes de la même manière que votre miroir de salle de bain inverse la chiralité de votre image par une réflexion à 180 degrés. Chaque rotation isoclinique de 360 degrés est comme si la surface de 24 cellules avait été enlevée comme un gant et retournée, faisant d'un gant droit un gant gauche (ou vice versa selon qu'il s'agissait d'un gant gauche ou d'un gant gauche). droite rotation isoclinic 360 degrés).
Dans une simple rotation des 24 cellules dans un plan hexagonal, chaque sommet du plan tourne d'abord le long d'un bord jusqu'à un sommet adjacent distant de 60 degrés. Mais dans une rotation isocline dans deux plans hexagonaux complètement orthogonaux, chaque sommet tourne d'abord vers un sommet à deux longueurs d'arête (en diagonale) dans un plan hexagonal différent. Les géodésiques hélicoïdales de la rotation à double hexagone passent par un sommet sur deux, se croisant entre les plans centraux. Même si tous les sommets et tous les hexagones tournent en même temps, une rotation de 360 degrés n'atteint que la moitié des sommets des 24 cellules. Après 360 degrés, chaque hélice a traversé 6 sommets, mais n'est pas revenue au sommet où elle est partie en formant un hexagone fermé. Chaque plan central (chaque hexagone ou carré dans les 24 cellules) a tourné à 360 degrés et a été incliné latéralement sur 360 degrés pour revenir à sa position d'origine, mais l' orientation des 24 cellules dans l'espace 4 dans lequel elles sont intégrées est maintenant différent. Étant donné que les 24 cellules sont maintenant à l'envers, si la rotation isocline se poursuit dans la même direction sur 360 degrés supplémentaires , les sommets mobiles passeront par l'autre moitié des sommets qu'ils ont manqués lors du premier tour (les sommets antipodaux de la ceux qu'ils ont frappé la première fois, sur leur face arrière), et chaque géodésique isoclinic seront arrivons au sommet , il a quitté, en formant une fermeture dodécagone . Il faut une rotation isocline de 720 degrés pour chaque géodésique isocline dodécagonale pour compléter un circuit à travers les 12 sommets qui s'y trouvent en s'enroulant deux fois autour des 24 cellules, ramenant les 24 cellules à son orientation chirale d'origine.
Deux plans sont également appelés isocliniques si une rotation isocline les rapproche. Les plans isocliniques sont précisément ces plans centraux avec des grands cercles géodésiques parallèles à Clifford. Les grands cercles parallèles de Clifford ne se coupent pas, donc les polygones des grands cercles isocliniques ont des sommets disjoints. Dans les 24 cellules, chaque plan central hexagonal est isocline à trois autres, et chaque plan central carré est isocline à cinq autres. Nous pouvons choisir 4 grands hexagones mutuellement isocliniques (parallèles à Clifford) (quatre manières différentes) couvrant les 24 sommets des 24 cellules une seule fois. Nous pouvons choisir 6 grands carrés mutuellement isocliniques (parallèles à Clifford) (trois manières différentes) couvrant les 24 sommets des 24 cellules une seule fois.
Polytopes parallèles de Clifford
Les polygones de grand cercle à deux dimensions ne sont pas les seuls polytopes des 24 cellules qui sont parallèles au sens de Clifford. Les polytopes congruents de 2, 3 ou 4 dimensions peuvent être dits Clifford parallèles en 4 dimensions si leurs sommets correspondants sont tous à la même distance les uns des autres dans les 4 directions de coordonnées. Les trois 16 cellules inscrites dans les 24 cellules sont des parallèles de Clifford. Les polytopes parallèles de Clifford sont des polytopes complètement disjoints . Une rotation isoclinique de 60 degrés dans des plans hexagonaux amène chaque 16 cellules à une 16 cellules disjointes. Comme toutes les doubles rotations , les rotations isocliniques se présentent sous deux formes chirales : il y a une 16-cellule disjointe à gauche de chaque 16-cellule, et une autre à sa droite .
Tous les 4-polytopes parallèles de Clifford sont liés par une rotation isocline, mais tous les polytopes isocliniques ne sont pas des parallèles de Clifford (complètement disjoints). Les trois 8 cellules dans les 24 cellules sont isocliniques mais pas parallèles à Clifford. Comme les 16 cellules, elles sont tournées de 60 degrés de manière isocline les unes par rapport aux autres, mais leurs sommets ne sont pas tous disjoints (et donc pas tous équidistants). Chaque sommet se trouve dans deux des trois 8 cellules (comme chaque 16 cellules se trouve dans deux des trois 8 cellules).
Les rotations isocliniques relient les 4-polytopes réguliers convexes les uns aux autres. Une rotation isoclinique d'une seule cellule de 16 générera une cellule de 24. Une simple rotation d'une seule cellule de 16 ne le fera pas, car ses sommets n'atteindront aucun des deux autres sommets de 16 cellules au cours de la rotation. Une rotation isoclinique des 24 cellules générera les 600 cellules, et une rotation isoclinique des 600 cellules générera les 120 cellules. (Ou ils peuvent tous être générés directement par des rotations isocliniques de la cellule 16, générant des copies isocliniques d'elle-même.) Les 4 polytopes réguliers convexes s'emboîtent les uns dans les autres et se cachent les uns à côté des autres dans les espaces parallèles de Clifford qui composent les 3 -sphère. Pour un objet de plus d'une dimension, la seule façon d'accéder directement à ces sous-espaces parallèles est par rotation isocline.
Projections
Projections parallèles
La projection parallèle au sommet en premier des 24 cellules dans l'espace tridimensionnel a une enveloppe dodécaédrique rhombique . Douze des 24 cellules octaédriques se projettent par paires sur six dipyramides carrées qui se rencontrent au centre du dodécaèdre rhombique. Les 12 cellules octaédriques restantes se projettent sur les 12 faces rhombiques du dodécaèdre rhombique.
La projection parallèle de la première cellule des 24 cellules dans l'espace tridimensionnel a une enveloppe cuboctaédrique . Deux des cellules octaédriques, la plus proche et la plus éloignée du spectateur le long de l' axe w , se projettent sur un octaèdre dont les sommets se trouvent au centre des faces carrées du cuboctaèdre. Autour de cet octaèdre central se trouvent les projections de 16 autres cellules, ayant 8 paires qui se projettent chacune sur l'un des 8 volumes compris entre une face triangulaire de l'octaèdre central et la face triangulaire la plus proche du cuboctaèdre. Les 6 cellules restantes se projettent sur les faces carrées du cuboctaèdre. Cela correspond à la décomposition du cuboctaèdre en un octaèdre régulier et 8 octaèdres irréguliers mais égaux, chacun ayant la forme de l'enveloppe convexe d'un cube avec deux sommets opposés supprimés.
La projection parallèle à bord en premier a une enveloppe dipyramidale hexagonale allongée , et la projection parallèle à face en premier a une enveloppe bi- antiprismique hexagonale non uniforme .
Projections en perspective
La projection en perspective du sommet en premier des 24 cellules dans l'espace tridimensionnel a une enveloppe hexaédrique tétrakis . La disposition des cellules dans cette image est similaire à l'image sous projection parallèle.
La séquence d'images suivante montre la structure de la projection en perspective de la première cellule des 24 cellules en 3 dimensions. Le point de vue 4D est placé à une distance de cinq fois le rayon du centre du sommet des 24 cellules.
 Coupe transversale animée de 24 cellules |
||
 Une projection 3D stéréoscopique d'un icsitetrachore (24 cellules). |
||
|
Projection orthogonale isométrique de : 8 cellules (Tesseract) + 16 cellules = 24 cellules |
||
Projections orthogonales
| Avion Coxeter | F 4 | |
|---|---|---|
| Graphique |

|
|
| Symétrie dièdre | [12] | |
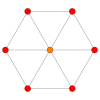
| Avion Coxeter | B 3 / A 2 (a) | B 3 / A 2 (b) |
| Graphique |
|

|
| Symétrie dièdre | [6] | [6] |
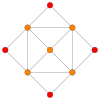
| Avion Coxeter | B 4 | B 2 / A 3 |
| Graphique |

|
|
| Symétrie dièdre | [8] | [4] |
Visualisation
Les 24 cellules sont délimitées par 24 cellules octaédriques . À des fins de visualisation, il est pratique que l'octaèdre ait des faces parallèles opposées (un trait qu'il partage avec les cellules du tesseract et du 120-cell ). On peut empiler des octaèdres face à face dans un courbée en ligne droite dans la direction quatrième en un grand cercle avec une circonférence de 6 cellules. Les emplacements des cellules se prêtent à une description hypersphérique . Choisissez une cellule arbitraire et nommez-la " Pôle Nord ". Huit méridiens du grand cercle (deux cellules de long) rayonnent en 3 dimensions, convergeant vers la 3e cellule " Pôle Sud ". Ce squelette représente 18 des 24 cellules (2 + 8 × 2 ). Voir le tableau ci-dessous.
Il y a un autre grand cercle connexe dans les 24 cellules, le dual de celui ci-dessus. Un chemin qui traverse 6 sommets uniquement le long des arêtes réside dans le dual de ce polytope, qui est lui-même puisqu'il est auto dual. Ce sont les géodésiques hexagonales décrites ci-dessus . On peut facilement suivre ce chemin dans un rendu de la section efficace du cuboctaèdre équatorial .
En partant du pôle Nord, nous pouvons construire les 24 cellules en 5 couches latitudinales. À l'exception des pôles, chaque couche représente une 2-sphère distincte, l'équateur étant une grande 2-sphère. Les cellules équatoriales dans le tableau suivant sont interstitielles par rapport aux cellules du grand cercle méridien. Les cellules interstitielles "équatoriales" touchent les cellules méridiennes au niveau de leurs faces. Ils se touchent, et les cellules polaires à leurs sommets. Ce dernier sous-ensemble de huit cellules non méridiennes et polaires a la même position relative les unes par rapport aux autres que les cellules d'un tesseract (8 cellules), bien qu'elles se touchent à leurs sommets au lieu de leurs faces.
| Couche # | Nombre de cellules | La description | Colatitude | Région |
|---|---|---|---|---|
| 1 | 1 cellule | pôle Nord | 0° | Hémisphère nord |
| 2 | 8 cellules | Première couche de cellules méridiennes | 60° | |
| 3 | 6 cellules | Non méridien / interstitiel | 90° | Équateur |
| 4 | 8 cellules | Deuxième couche de cellules méridiennes | 120° | Hémisphère sud |
| 5 | 1 cellule | pôle Sud | 180° | |
| Le total | 24 cellules | |||
Les 24 cellules peuvent être divisées en ensembles disjoints de cellules de quatre de ces anneaux de grand cercle à 6 cellules, formant une fibration de Hopf discrète de quatre anneaux imbriqués. Un anneau est "vertical", englobant les cellules polaires et quatre cellules méridiennes. Les trois autres anneaux englobent chacun deux cellules équatoriales et quatre cellules méridiennes, deux de l'hémisphère nord et deux de l'hémisphère sud.
Notez que ce chemin de grand cercle hexagonal implique que l'angle intérieur/dièdre entre les cellules adjacentes est de 180 - 360/6 = 120 degrés. Cela suggère que vous pouvez empiler de manière adjacente exactement trois 24 cellules dans un plan et former un nid d'abeilles 4-D de 24 cellules comme décrit précédemment.
On peut aussi suivre un grand cercle de route, à travers les octaèdres de sommets des opposés, qui est quatre cellules longues. Ce sont les géodésiques carrées le long des quatre cordes √ 2 décrites ci-dessus . Ce chemin correspond à parcourir en diagonale les carrés de la section transversale du cuboctaèdre. Le 24 cellules est le seul polytope régulier dans plus de deux dimensions où vous pouvez traverser un grand cercle uniquement à travers les sommets opposés (et l'intérieur) de chaque cellule. Ce grand cercle est auto-dual. Ce chemin a été évoqué ci-dessus concernant l'ensemble des 8 cellules non méridiennes (équatoriales) et polaires. Les 24 cellules peuvent être réparties en trois sous-ensembles de 8 cellules, chacun ayant l'organisation d'un tesseract. Chacun de ces sous-ensembles peut être encore réparti en deux chaînes de grand cercle imbriquées, de quatre cellules de long. Collectivement, ces trois sous-ensembles produisent maintenant une autre fibration de Hopf discrète à six anneaux.
Trois constructions du groupe Coxeter
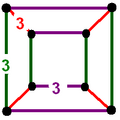
Il existe deux formes de symétrie inférieure des 24 cellules, dérivées sous forme de 16 cellules rectifiées , avec la symétrie B 4 ou [3,3,4] dessinée en bicolore avec 8 et 16 cellules octaédriques . Enfin il peut être construit à partir de la symétrie D 4 ou [3 1,1,1 ], et dessiné en tricolore avec 8 octaèdres chacun.
| Trois filets des 24 cellules avec des cellules colorées par la symétrie D 4 , B 4 et F 4 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Demitesseract rectifié | 16 cellules rectifiées | 24 cellules régulières | |||||||||
| D 4 , [3 1,1,1 ], ordre 192 | B 4 , [3,3,4], ordre 384 | F 4 , [3,4,3], ordre 1152 | |||||||||

|
|||||||||||
| Trois ensembles de 8 cellules tétraédriques rectifiées | Un ensemble de 16 cellules tétraédriques rectifiées et un ensemble de 8 cellules octaédriques . | Un ensemble de 24 cellules octaédriques | |||||||||
|
Figure de sommet (Chaque arête correspond à une face triangulaire, colorée par arrangement de symétrie) |
|||||||||||
|

|

|
|||||||||
Polygones complexes associés
Le polygone complexe régulier 4 {3} 4 ,![]()
![]()
![]() ou
ou ![]()
![]()
![]() contient les 24 sommets des 24 cellules et 24 4 arêtes qui correspondent aux carrés centraux de 24 des 48 cellules octaédriques. Sa symétrie est 4 [3] 4 , ordre 96.
contient les 24 sommets des 24 cellules et 24 4 arêtes qui correspondent aux carrés centraux de 24 des 48 cellules octaédriques. Sa symétrie est 4 [3] 4 , ordre 96.
Le polytope complexe régulier 3 {4} 3 ,![]()
![]()
![]() ou
ou ![]()
![]()
![]() , in a une représentation réelle sous forme de 24 cellules dans un espace à 4 dimensions. 3 {4} 3 a 24 sommets et 24 3-arêtes. Sa symétrie est 3 [4] 3 , ordre 72.
, in a une représentation réelle sous forme de 24 cellules dans un espace à 4 dimensions. 3 {4} 3 a 24 sommets et 24 3-arêtes. Sa symétrie est 3 [4] 3 , ordre 72.
4-polytopes apparentés
Plusieurs 4-polytopes uniformes peuvent être dérivés des 24 cellules par troncature :
- la troncature à 1/3 de la longueur du bord donne les 24 cellules tronquées ;
- tronquer à 1/2 de la longueur du bord donne les 24 cellules rectifiées ;
- et en tronquant à la moitié de la profondeur jusqu'aux 24 cellules doubles, on obtient les 24 cellules tronquées , qui sont transitives par les cellules .
Les 96 arêtes des 24 cellules peuvent être divisées en nombre d' or pour produire les 96 sommets du snub 24-cell . Cela se fait en plaçant d'abord des vecteurs le long des bords des 24 cellules de telle sorte que chaque face bidimensionnelle soit délimitée par un cycle, puis en partitionnant de la même manière chaque bord dans le nombre d'or le long de la direction de son vecteur. Une modification analogue à un octaèdre produit un icosaèdre , ou « octaèdre snub ».
La cellule 24 est l'unique polytope euclidien régulier auto-dual convexe qui n'est ni un polygone ni un simplexe . L'assouplissement de la condition de convexité admet deux autres figures : la grande cellule 120 et la grande cellule étoilée 120 . Avec lui-même, il peut former un composé polytopique : le composé de deux 24-cellules .
Polytopes uniformes associés
| D 4 polychore uniforme | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
|
|
|
|
|
|
|
||||

|

|

|

|

|

|

|

|
||||
|
{3,3 1,1 } h{4,3,3} |
2r{3,3 1,1 } h 3 {4,3,3} |
t{3,3 1,1 } h 2 {4,3,3} |
2t{3,3 1,1 } h 2,3 {4,3,3} |
r{3,3 1,1 } {3 1,1,1 }={3,4,3} |
rr{3,3 1,1 } r{3 1,1,1 }=r{3,4,3} |
tr{3,3 1,1 } t{3 1,1,1 }=t{3,4,3} |
sr{3,3 1,1 } s{3 1,1,1 }=s{3,4,3} |
||||
| Polytopes de la famille à 24 cellules | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Nom | 24 cellules | 24 cellules tronquées | snob 24-cell | 24 cellules rectifiées | 24 cellules cantellées | 24 cellules tronquées | 24 cellules cantitrées | 24 cellules runcinées | 24 cellules tronquées | 24 cellules omnitronquées | |
|
Symbole Schläfli |
{3,4,3} | t 0,1 {3,4,3} t{3,4,3} |
s{3,4,3} | t 1 {3,4,3} r{3,4,3} |
t 0,2 {3,4,3} rr{3,4,3} |
t 1,2 {3,4,3} 2t{3,4,3} |
t 0,1,2 {3,4,3} tr{3,4,3} |
t 0,3 {3,4,3} | t 0,1,3 {3,4,3} | t 0,1,2,3 {3,4,3} | |
|
Diagramme de Coxeter |
|
|
|
|
|
|
|
|
|
|
|
|
Diagramme de Schlegel |

|

|

|

|

|

|

|

|

|

|
|
| F 4 |

|

|

|

|

|

|

|

|

|

|
|
| B 4 |

|

|

|

|

|

|

|

|

|

|
|
| B 3 (a) |

|

|

|

|

|

|

|

|

|

|
|
| B 3 (b) |

|

|

|

|

|

|
|||||
| B 2 |

|

|

|

|

|

|

|

|

|

|
|
Le 24-cell peut également être dérivé comme un 16-cell rectifié :
| Polytopes de symétrie B4 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Nom | tesseract |
tesseract rectifié |
tesseract tronqué |
tesseract cantellé |
tesseract runciné |
tesseract tronqué |
tesseract tronqué |
tesseract tronqué |
tesseract omnitronqué |
||
|
Diagramme de Coxeter |
|
= |
|
|
|
= |
|
|
|
||
|
Symbole Schläfli |
{4,3,3} | t 1 {4,3,3} r{4,3,3} |
t 0,1 {4,3,3} t{4,3,3} |
t 0,2 {4,3,3} rr{4,3,3} |
t 0,3 {4,3,3} | t 1,2 {4,3,3} 2t{4,3,3} |
t 0,1,2 {4,3,3} tr{4,3,3} |
t 0,1,3 {4,3,3} | t 0,1,2,3 {4,3,3} | ||
|
Diagramme de Schlegel |

|

|

|

|

|

|

|

|

|
||
| B 4 |

|

|

|

|

|

|

|

|

|
||
| Nom | 16 cellules |
16 cellules rectifiées |
16 cellules tronquées |
à 16 cellules cantellées |
16 cellules runcinées |
16 cellules tronquées |
cantitroncé 16 cellules |
tronqué à 16 alvéoles |
16 cellules omnitronquées |
||
|
Diagramme de Coxeter |
= |
= |
= |
= |
|
= |
= |
|
|
||
|
Symbole Schläfli |
{3,3,4} | t 1 {3,3,4} r{3,3,4} |
t 0,1 {3,3,4} t{3,3,4} |
t 0,2 {3,3,4} rr{3,3,4} |
t 0,3 {3,3,4} | t 1,2 {3,3,4} 2t{3,3,4} |
t 0,1,2 {3,3,4} tr{3,3,4} |
t 0,1,3 {3,3,4} | t 0,1,2,3 {3,3,4} | ||
|
Diagramme de Schlegel |

|

|

|

|

|

|

|

|

|
||
| B 4 |

|

|

|

|

|

|

|

|

|
||
| {3, p ,3} polytopes | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Espacer | S 3 | H 3 | |||||||||
| Former | Fini | Compact | Paracompacte | Non compact | |||||||
| {3, p ,3} | {3,3,3} | {3,4,3} | {3,5,3} | {3,6,3} | {3,7,3} | {3,8,3} | ... {3,∞,3} | ||||
| Image |

|

|

|

|

|

|

|
||||
| Cellules |
 {3,3} |
 {3,4} |
 {3,5} |
 {3,6} |
 {3,7} |
 {3,8} |
 {3,∞} |
||||
Figure de sommet |
 {3,3} |
 {4,3} |
 {5,3} |
 {6,3} |
 {7,3} |
 {8,3} |
 {∞,3} |
||||
Voir également
Remarques
Citations
Les références
- Kepler, Johannes (1619). Harmonices Mundi (L'Harmonie du Monde) . Johann Planck.
- Coxeter, HSM (1973) [1948]. Polytopes réguliers (3e éd.). New York : Douvres.
- Coxeter, HSM (1991), Regular Complex Polytopes (2e éd.), Cambridge: Cambridge University Press
-
Coxeter, HSM (1995), Sherk, F. Arthur; McMullen, Peter; Thompson, Anthony C.; Weiss, Asia Ivic (eds.), Kaleidoscopes: Selected Writings of HSM Coxeter (2e ed.), Wiley-Interscience Publication, ISBN 978-0-471-01003-6
- (Document 3) HSM Coxeter, Deux aspects des 24 cellules régulières en quatre dimensions
- (Article 22) HSM Coxeter, Polytopes réguliers et semi-réguliers I , [Math. Zeit. 46 (1940) 380-407, MR 2,10]
- (Document 23) HSM Coxeter, Polytopes réguliers et semi-réguliers II , [Math. Zeit. 188 (1985) 559-591]
- (Document 24) HSM Coxeter, Polytopes réguliers et semi-réguliers III , [Math. Zeit. 200 (1988) 3-45]
- Stillwell, John (janvier 2001). « L'histoire de la 120-Cellule » (PDF) . Avis de l'AMS . 48 (1) : 17-25.
- Johnson, Norman (2018), Géométries et transformations , Cambridge : Cambridge University Press, ISBN 978-1-107-10340-5
- Johnson, Norman (1991), Uniform Polytopes (éd. Manuscrit)
- Johnson, Norman (1966), The Theory of Uniform Polytopes and Honeycombs (Ph.D. ed.)
- Weisstein, Eric W. "24 cellules" . MathWorld . (également sous Icositetrachoron)
- Klitzing, Richard. "Polytopes uniformes 4D (polychora) x3o4o3o - ico" .
- Olchevski, Georges. "Icositetrachoron" . Glossaire de l'hyperespace . Archivé de l'original le 4 février 2007.
- Ghyka, Matila (1977). La géométrie de l'art et de la vie . New York : Publications de Douvres. ISBN 978-0-486-23542-4.
- Banchoff, Thomas F. (2013). « Les décompositions de tore de polytopes réguliers dans l'espace 4 ». Dans Sénéchal, Marjorie (éd.). Façonner l'espace . Springer New York. p. 257 –266. doi : 10.1007/978-0-387-92714-5_20 . ISBN 978-0-387-92713-8.
- Copher, Jessica (2019). "Sommes et produits des longueurs de corde au carré des polytopes réguliers". arXiv : 1903.06971 [ math.MG ].
- van Ittersum, Clara (2020). Groupes de symétrie de polytopes réguliers en trois et quatre dimensions (Thèse). Université de technologie de Delft .
- Kim, Heuna; Roté, G. (2016). "Test de congruence des ensembles de points en 4 dimensions". arXiv : 1603.07269 [ cs.CG ].
- Waegell, Mardochée ; Aravind, PK (2009-11-12). « Noncolorations critiques des 600 cellules prouvant le théorème de Bell-Kochen-Specker ». Journal de Physique A : Mathématique et Théorique . 43 (10) : 105304. arXiv : 0911.2289 . doi : 10.1088/1751-8113/43/10/105304 . S2CID 118501180 .
Liens externes
- Animations 24 cellules
- 24 cellules en projections stéréographiques
- Description et diagrammes de 24 cellules
- Les dodécagones de Petrie dans les 24 cellules : logiciels de mathématiques et d'animation