1  ₄₂ polytope -1 ₄₂ polytope

4 21	1 42	2 41
Rectifié 4 21	Rectifié 1 42	Rectifié 2 41
Birectifié 4 21	Trirectifié 4 21
Projections orthogonales dans le plan de Coxeter E 6

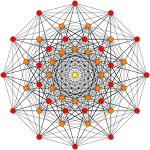
En géométrie à 8 dimensions , le 1 ₄₂ est un 8-polytope uniforme , construit dans la symétrie du groupe E ₈ .

Son symbole de Coxeter est 1 ₄₂ , décrivant son diagramme de Coxeter-Dynkin bifurquant , avec un seul anneau à la fin des séquences à 1 nœud.

Le 1 ₄₂ rectifié est construit par des points aux bords médians du 1 ₄₂ et est le même que le 2 ₄₁ birectifié et le 4 ₂₁ quadrirectifié .

Ces polytopes font partie d'une famille de 255 (2 ⁸  − 1) polytopes uniformes convexes en 8 dimensions, constitués de facettes polytopiques uniformes et de figures de sommet , définies par toutes les permutations d'anneaux dans ce diagramme de Coxeter-Dynkin :.

1 ₄₂ polytope

1 42
Taper	Uniforme 8-polytope
Famille	1 polytope k2
Symbole Schläfli	{3,3 4,2 }
Symbole de Coxeter	1 42
Diagrammes de Coxeter
7-faces	2400 : 240 1 32 2160 1 41
6-faces	106080 : 6720 1 22 30240 1 31 69120 {3 5 }
5 visages	725760 :  60480 1 12 181440 1 21 483840 {3 4 }
4 faces	2298240 : 241920 1 02 604800 1 11 1451520 {3 3 }
Cellules	3628800 : 1209600 1 01 2419200 {3 2 }
Visages	2419200 {3}
Bords	483840
Sommets	17280
Figure de sommet	t 2 {3 6 }
Polygone de Pétrie	30-gon
Groupe Coxeter	E 8 , [3 4,2,1 ]
Propriétés	convexe

Le 1 ₄₂ est composé de 2400 facettes : 240 1 ₃₂ polytopes, et 2160 7-demicubes ( 1 ₄₁ ). Sa figure de sommet est un 7-simplex birectifié .

Ce polytope, avec le demiocteract , peut tesseler l' espace à 8 dimensions, représenté par le symbole 1 ₅₂ , et le diagramme de Coxeter-Dynkin :.

Noms alternatifs

• EL Elte (1912) a exclu ce polytope de sa liste de polytopes semi-réguliers, car il a plus de deux types de 6 faces, mais selon son schéma de nommage, il serait appelé V ₁₇₂₈₀ pour ses 17280 sommets.
• Coxeter l'a nommé 1 ₄₂ pour son diagramme de Coxeter-Dynkin bifurquant , avec un seul anneau à l'extrémité de la branche à 1 nœud.
• Diacositetracont-dischiliahectohexaconta-zetton (acronyme bif ) - 240-2160 polyzetton à facettes (Jonathan Bowers)

Coordonnées

Les 17280 sommets peuvent être définis comme des permutations de signe et d'emplacement de :

Toutes les combinaisons de signes (32) : (280×32=8960 sommets)

(4, 2, 2, 2, 2, 0, 0, 0)

La moitié des combinaisons de signes (128) : ((1+8+56)×128=8320 sommets)

(2, 2, 2, 2, 2, 2, 2, 2)

(5, 1, 1, 1, 1, 1, 1, 1)

(3, 3, 3, 1, 1, 1, 1, 1)

La longueur d'arête est de 2 √ 2 dans cet ensemble de coordonnées, et le rayon de polytope est 4 √ 2 .

Construction

Il est créé par une construction de Wythoff sur un ensemble de 8 miroirs hyperplans dans un espace à 8 dimensions.

L'information de la facette peut être extraite de son diagramme de Coxeter-Dynkin :.

La suppression du nœud à l'extrémité de la branche de longueur 2 laisse le demi-cube 7 , 1 ₄₁ ,.

La suppression du nœud à l'extrémité de la branche 4 longueurs laisse le 1 ₃₂ ,.

La figure de sommet est déterminée en supprimant le nœud annelé et en faisant sonner le nœud voisin. Cela rend le 7-simplex birectifié , 0 ₄₂ ,.

Vu dans une matrice de configuration , les nombres d'éléments peuvent être dérivés par suppression de miroirs et ratios d' ordres de groupe de Coxeter .

E 8		k- visage	f k	f 0	f 1	f 2	f 3		f 4			f 5			f 6			f 7		k- figure	Remarques
Un 7		( )	f 0	17280	56	420	280	560	70	280	420	56	168	168	28	56	28	8	8	2r{3 6 }	E 8 /A 7 = 192*10!/8! = 17280
A 4 A 2 A 1		{ }	f 1	2	483840	15	15	30	5	30	30	dix	30	15	dix	15	3	5	3	{3}x{3,3,3}	E 8 /A 4 A 2 A 1 = 192*10!/5!/2/2 = 483840
A 3 A 2 A 1		{3}	f 2	3	3	2419200	2	4	1	8	6	4	12	4	6	8	1	4	2	{3.3}v{ }	E 8 /A 3 A 2 A 1 = 192*10!/4!/3!/2 = 2419200
Un 3 Un 3		1 10	f 3	4	6	4	1209600	*	1	4	0	4	6	0	6	4	0	4	1	{3,3}v( )	E 8 /A 3 A 3 = 192*10!/4!/4! = 1209600
A 3 A 2 A 1				4	6	4	*	2419200	0	2	3	1	6	3	3	6	1	3	2	{3}v{ }	E 8 /A 3 A 2 A 1 = 192*10!/4!/3!/2 = 2419200
A 4 A 3		1 20	f 4	5	dix	dix	5	0	241920	*	*	4	0	0	6	0	0	4	0	{3,3}	E 8 /A 4 A 3 = 192*10!/4!/4! = 241920
D 4 A 2		1 11		8	24	32	8	8	*	604800	*	1	3	0	3	3	0	3	1	{3}v( )	E 8 /D 4 A 2 = 192*10!/8/4!/3! = 604800
A 4 A 1 A 1		1 20		5	dix	dix	0	5	*	*	1451520	0	2	2	1	4	1	2	2	{ }v{ }	E 8 /A 4 A 1 A 1 = 192*10!/5!/2/2 = 1451520
D 5 A 2		1 21	f 5	16	80	160	80	40	16	dix	0	60480	*	*	3	0	0	3	0	{3}	E 8 /D 5 A 2 = 192*10!/16/5!/3! = 40480
D 5 A 1				16	80	160	40	80	0	dix	16	*	181440	*	1	2	0	2	1	{ }v( )	E 8 /D 5 A 1 = 192*10!/16/5!/2 = 181440
Un 5 Un 1		1 30		6	15	20	0	15	0	0	6	*	*	483840	0	2	1	1	2		E 8 /A 5 A 1 = 192*10!/6!/2 = 483840
E 6 A 1		1 22	f 6	72	720	2160	1080	1080	216	270	216	27	27	0	6720	*	*	2	0	{ }	E 8 /E 6 A 1 = 192*10!/72/6!/2 = 6720
D 6		1 31		32	240	640	160	480	0	60	192	0	12	32	*	30240	*	1	1		E 8 /D 6 = 192*10!/32/6! = 30240
Un 6 Un 1		1 40		7	21	35	0	35	0	0	21	0	0	7	*	*	69120	0	2		E 8 /A 6 A 1 = 192*10!/7!/2 = 69120
E 7		1 32	f 7	576	10080	40320	20160	30240	4032	7560	12096	756	1512	2016	56	126	0	240	*	( )	E 8 /E 7 = 192*10!/72/8! = 240
D 7		1 41		64	672	2240	560	2240	0	280	1344	0	84	448	0	14	64	*	2160		E 8 /D 7 = 192*10!/64/7! = 2160

Projections

Montré en projection 3D en utilisant les vecteurs de base [u,v,w] donnant la symétrie H3 : Les 17280 1 ₄₂ sommets polytopiques projetés sont triés et comptés par leur norme 3D générant les coques de plus en plus transparentes pour chaque ensemble de normes comptées. Notez que les deux dernières coques extérieures sont une combinaison de deux dodécaèdres superposés (40) et d'un rhombicosidodécaèdre non uniforme (60).

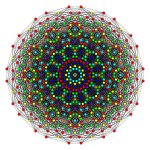
Les projections orthographiques sont présentées pour les sous-symétries de E ₈ : E ₇ , E ₆ , B ₈ , B ₇ , B ₆ , B ₅ , B ₄ , B ₃ , B ₂ , A ₇ et A ₅ plans de Coxeter , comme ainsi que deux autres plans de symétrie d'ordre 20 et 24. Les sommets sont représentés par des cercles, colorés par leur ordre de chevauchement dans chaque plan projectif.

E8 [30]	E7 [18]	E6 [12]
(1)	(1,3,6)	(8,16,24,32,48,64,96)
[20]	[24]	[6]
		(1,2,3,4,5,6,7,8,10,11,12,14,16,18,19,20)

D3 / B2 / A3 [4]	D4 / B3 / A2 [6]	D5 / B4 [8]
(32 160 192 240 480 512 832 960)	(72 216 432 720 864 1080)	(8,16,24,32,48,64,96)
D6 / B5 / A4 [10]	D7 / B6 [12]	D8 / B7 / A6 [14]
B8 [16/2]	A5 [6]	A7 [8]

Polytopes et nids d'abeilles associés

1 k2 chiffres en n dimensions
Espacer	Fini						euclidien	Hyperbolique
m	3	4	5	6	7	8	9	dix
Groupe Coxeter	E 3 =A 2 A 1	E 4 = A 4	E 5 = D 5	E 6	E 7	E 8	E 9 = = E 8 +${\displaystyle {\tilde {E}}_{8}}$	E 10 = = E 8 ++${\displaystyle {\bar {T}}_{8}}$
Diagramme de Coxeter
Symétrie (ordre)	[3 -1,2,1 ]	[3 0,2,1 ]	[3 1,2,1 ]	[[3 2,2,1 ]]	[3 3,2,1 ]	[3 4,2,1 ]	[3 5,2,1 ]	[3 6,2,1 ]
Commander	12	120	1 920	103 680	2 903 040	696 729 600	??
Graphique							-	-
Nom	1 −1,2	1 02	1 12	1 22	1 32	1 42	1 52	1 62

1 ₄₂ polytope rectifié

Rectifié 1 42
Taper	Uniforme 8-polytope
Symbole Schläfli	t 1 {3,3 4,2 }
Symbole de Coxeter	0 421
Diagrammes de Coxeter
7-faces	196880
6-faces	382560
5 visages	2661120
4 faces	9072000
Cellules	16934400
Visages	16934400
Bords	7257600
Sommets	483840
Figure de sommet	{3,3,3}×{3}×{}
Groupe Coxeter	E 8 , [3 4,2,1 ]
Propriétés	convexe

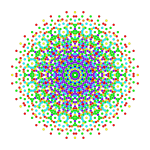
Le 1 ₄₂ rectifié _tire son nom d'une rectification du polytope 1 ₄₂ , avec des sommets positionnés sur les bords médians du 1 ₄₂ . On peut aussi l'appeler polytope 0 ₄₂₁ avec l'anneau au centre de 3 branches de longueur 4, 2 et 1.

Noms alternatifs

• 0 ₄₂₁ polytope
• Birectified 2 ₄₁ polytope
• Quadrirectified 4 ₂₁ polytope
• Diacositetracont-dischiliahectohexaconta-zetton rectifié en tant que polyzetton à facettes 240-2160 rectifié (acronyme buffy ) (Jonathan Bowers)

Construction

Il est créé par une construction de Wythoff sur un ensemble de 8 miroirs hyperplans dans un espace à 8 dimensions.

L'information de la facette peut être extraite de son diagramme de Coxeter-Dynkin :.

La suppression du nœud à l'extrémité de la branche de longueur 1 laisse le 7-simplex birectifié ,

La suppression du nœud à l'extrémité de la branche de longueur 2 laisse le cube 7 birectifié ,.

La suppression du nœud à l'extrémité de la branche 3-longueur laisse le rectifié 1 ₃₂ ,.

La figure de sommet est déterminée en supprimant le nœud annelé et en faisant sonner le nœud voisin. Cela rend le 5 cellules - triangle prisme duoprisme,.

Vu dans une matrice de configuration , les nombres d'éléments peuvent être dérivés par suppression de miroirs et ratios d' ordres de groupe de Coxeter .

E 8		k- visage	f k	f 0	f 1	f 2			f 3					f 4						f 5						f 6					f 7			k- figure
A 4 A 2 A 1		( )	f 0	483840	30	30	15	60	dix	15	60	30	60	5	20	30	60	30	30	dix	20	30	30	15	6	dix	dix	15	6	3	5	2	3	{3,3,3}x{3,3}x{}
A 3 A 1 A 1		{ }	f 1	2	7257600	2	1	4	1	2	8	4	6	1	4	8	12	6	4	4	6	12	8	4	1	6	4	8	2	1	4	1	2
A 3 A 2		{3}	f 2	3	3	4838400	*	*	1	1	4	0	0	1	4	4	6	0	0	4	6	6	4	0	0	6	4	4	1	0	4	1	1
A 3 A 2 A 1				3	3	*	2419200	*	0	2	0	4	0	1	0	8	0	6	0	4	0	12	0	4	0	6	0	8	0	1	4	0	2
A 2 A 2 A 1				3	3	*	*	9676800	0	0	2	1	3	0	1	2	6	3	3	1	3	6	6	3	1	3	3	6	2	1	3	1	2
Un 3 Un 3		0 200	f 3	4	6	4	0	0	1209600	*	*	*	*	1	4	0	0	0	0	4	6	0	0	0	0	6	4	0	0	0	4	1	0
		0 110		6	12	4	4	0	*	1209600	*	*	*	1	0	4	0	0	0	4	0	6	0	0	0	6	0	4	0	0	4	0	1
A 3 A 2				6	12	4	0	4	*	*	4838400	*	*	0	1	1	3	0	0	1	3	3	3	0	0	3	3	3	1	0	3	1	1
A 3 A 2 A 1				6	12	0	4	4	*	*	*	2419200	*	0	0	2	0	3	0	1	0	6	0	3	0	3	0	6	0	1	3	0	2
A 3 A 1 A 1		0 200		4	6	0	0	4	*	*	*	*	7257600	0	0	0	2	1	2	0	1	2	4	2	1	1	2	4	2	1	2	1	2
A 4 A 3		0 210	f 4	dix	30	20	dix	0	5	5	0	0	0	241920	*	*	*	*	*	4	0	0	0	0	0	6	0	0	0	0	4	0	0
A 4 A 2				dix	30	20	0	dix	5	0	5	0	0	*	967680	*	*	*	*	1	3	0	0	0	0	3	3	0	0	0	3	1	0
D 4 A 2		0 111		24	96	32	32	32	0	8	8	8	0	*	*	604800	*	*	*	1	0	3	0	0	0	3	0	3	0	0	3	0	1
A 4 A 1		0 210		dix	30	dix	0	20	0	0	5	0	5	*	*	*	2903040	*	*	0	1	1	2	0	0	1	2	2	1	0	2	1	1
A 4 A 1 A 1				dix	30	0	dix	20	0	0	0	5	5	*	*	*	*	1451520	*	0	0	2	0	2	0	1	0	4	0	1	2	0	2
A 4 A 1		0 300		5	dix	0	0	dix	0	0	0	0	5	*	*	*	*	*	2903040	0	0	0	2	1	1	0	1	2	2	1	1	1	2
D 5 A 2		0 211	f 5	80	480	320	160	160	80	80	80	40	0	16	16	dix	0	0	0	60480	*	*	*	*	*	3	0	0	0	0	3	0	0	{3}
Un 5 Un 1		0 220		20	90	60	0	60	15	0	30	0	15	0	6	0	6	0	0	*	483840	*	*	*	*	1	2	0	0	0	2	1	0	{ }v()
D 5 A 1		0 211		80	480	160	160	320	0	40	80	80	80	0	0	dix	16	16	0	*	*	181440	*	*	*	1	0	2	0	0	2	0	1
Un 5		0 310		15	60	20	0	60	0	0	15	0	30	0	0	0	6	0	6	*	*	*	967680	*	*	0	1	1	1	0	1	1	1	( )v( )v()
Un 5 Un 1				15	60	0	20	60	0	0	0	15	30	0	0	0	0	6	6	*	*	*	*	483840	*	0	0	2	0	1	1	0	2	{ }v()
		0 400		6	15	0	0	20	0	0	0	0	15	0	0	0	0	0	6	*	*	*	*	*	483840	0	0	0	2	1	0	1	2
E 6 A 1		0 221	f 6	720	6480	4320	2160	4320	1080	1080	2160	1080	1080	216	432	270	432	216	0	27	72	27	0	0	0	6720	*	*	*	*	2	0	0	{ }
Un 6		0 320		35	210	140	0	210	35	0	105	0	105	0	21	0	42	0	21	0	7	0	7	0	0	*	138240	*	*	*	1	1	0
D 6		0 311		240	1920	640	640	1920	0	160	480	480	960	0	0	60	192	192	192	0	0	12	32	32	0	*	*	30240	*	*	1	0	1
Un 6		0 410		21	105	35	0	140	0	0	35	0	105	0	0	0	21	0	42	0	0	0	7	0	7	*	*	*	138240	*	0	1	1
Un 6 Un 1				21	105	0	35	140	0	0	0	35	105	0	0	0	0	21	42	0	0	0	0	7	7	*	*	*	*	69120	0	0	2
E 7		0 321	f 7	10080	120960	80640	40320	120960	20160	20160	60480	30240	60480	4032	12096	7560	24192	12096	12096	756	4032	1512	4032	2016	0	56	576	126	0	0	240	*	*	( )
Un 7		0 420		56	420	280	0	560	70	0	280	0	420	0	56	0	168	0	168	0	28	0	56	0	28	0	8	0	8	0	*	17280	*
D 7		0 411		672	6720	2240	2240	8960	0	560	2240	2240	6720	0	0	280	1344	1344	2688	0	0	84	448	448	448	0	0	14	64	64	*	*	2160

Projections

Des projections orthographiques sont présentées pour les sous-symétries des plans de Coxeter B ₆ , B ₅ , B ₄ , B ₃ , B ₂ , A ₇ et A ₅ . Les sommets sont représentés par des cercles, colorés par leur ordre de chevauchement dans chaque plan projectif.

(Les plans pour E ₈ : E ₇ , E ₆ , B ₈ , B ₇ , [24] ne sont pas affichés car trop grands pour être affichés.)

D3 / B2 / A3 [4]	D4 / B3 / A2 [6]	D5 / B4 [8]
D6 / B5 / A4 [10]	D7 / B6 [12]	[6]
A5 [6]	A7 [8]	[20]

Voir également

• Liste des polytopes E8

Remarques

Les références

• HSM Coxeter , Polytopes réguliers , 3e édition, Douvres New York, 1973
• Kaleidoscopes: Selected Writings of HSM Coxeter , édité par F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN  978-0-471-01003-6 [1]
  • (Document 24) HSM Coxeter, Polytopes réguliers et semi-réguliers III , [Math. Zeit. 200 (1988) 3-45]
• Klitzing, Richard. "Polyzette uniforme 8D" . o3o3o3x *c3o3o3o3o - bif, o3o3o3x *c3o3o3o3o - buffy