7-demicube - 7-demicube

Demihepteract (7-demicube)
Projection de polygones de Petrie
Type	Uniforme 7-polytope
Famille	demihypercube
Symbole de Coxeter	1 41
Symbole Schläfli	{3,3 4,1 } = h {4,3 5 } s {2 1,1,1,1,1,1 }
Diagrammes de Coxeter	=
6 faces	78	14 {3 1,3,1 } 64 {3 5 }
5 faces	532	84 {3 1,2,1 } 448 {3 4 }
4 faces	1624	280 {3 1,1,1 } 1344 {3 3 }
Cellules	2800	560 {3 1,0,1 } 2240 {} 3,3
Visages	2240	{3}
Bords	672
Sommets	64
Figure de sommet	Rectifié 6-simplex
Groupe de symétrie	J 7 , [3 4,1,1 ] = [1 + , 4,3 5 ] [2 6 ] +
Double	?
Propriétés	convexe

En géométrie , un demihepteract ou 7-demicube est un 7-polytope uniforme , construit à partir du 7-hypercube ( hepteract ) avec des sommets alternés supprimés. Il fait partie d'une famille dimensionnellement infinie de polytopes uniformes appelés demihypercubes .

EL Elte l'a identifié en 1912 comme un polytope semi-régulier, le marquant comme HM ₇ pour un polytope demi-mesure à 7 dimensions .

Coxeter a nommé ce polytope comme 1 ₄₁ de son diagramme de Coxeter , avec un anneau sur l'une des branches de 1 longueur,et le symbole Schläfli ou {3,3 ^4,1 }. ${\ displaystyle \ left \ {3 {\ begin {array} {l} 3,3,3,3 \\ 3 \ end {array}} \ right \}}$

Coordonnées cartésiennes

Les coordonnées cartésiennes des sommets d'un demihepteract centré à l'origine sont des moitiés alternées de l' hepteract :

(± 1, ± 1, ± 1, ± 1, ± 1, ± 1, ± 1)

avec un nombre impair de signes plus.

Images

projections orthographiques

Avion de Coxeter	B 7	D 7	D 6
Graphique
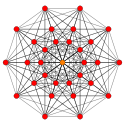
Symétrie dièdre	[14/2]	[12]	[dix]
Avion de Coxeter	D 5	D 4	D 3
Graphique
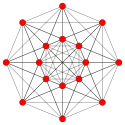
Symétrie dièdre	[8]	[6]	[4]
Avion de Coxeter	A 5	A 3
Graphique
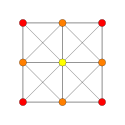
Symétrie dièdre	[6]	[4]

En tant que configuration

Cette matrice de configuration représente le 7-demicube. Les lignes et colonnes correspondent aux sommets, arêtes, faces, cellules, 4 faces, 5 faces et 6 faces. Les nombres diagonaux indiquent combien de chaque élément se produit dans tout le 7-demicube. Les nombres non diagonaux indiquent combien d'éléments de la colonne se trouvent dans ou à l'élément de la ligne.

Les nombres de vecteurs f diagonaux sont dérivés par la construction de Wythoff , en divisant l'ordre de groupe complet d'un ordre de sous-groupe en supprimant un miroir à la fois.

D 7		k -face	f k	f 0	f 1	f 2	f 3		f 4		f 5		f 6		k -figures	Remarques
A 6		()	f 0	64	21	105	35	140	35	105	21	42	7	7	0 41	D 7 / A 6 = 64 * 7! / 7! = 64
A 4 A 1 A 1		{}	f 1	2	672	dix	5	20	dix	20	dix	dix	5	2	{} × {3,3,3}	D 7 / A 4 A 1 A 1 = 64 * 7! / 5! / 2/2 = 672
A 3 A 2		1 00	f 2	3	3	2240	1	4	4	6	6	4	4	1	{3,3} v ()	D 7 / A 3 A 2 = 64 * 7! / 4! / 3! = 2240
A 3 A 3		1 01	f 3	4	6	4	560	*	4	0	6	0	4	0	{3,3}	D 7 / A 3 A 3 = 64 * 7! / 4! / 4! = 560
A 3 A 2		1 10		4	6	4	*	2240	1	3	3	3	3	1	{3} v ()	D 7 / A 3 A 2 = 64 * 7! / 4! / 3! = 2240
D 4 A 2		1 11	f 4	8	24	32	8	8	280	*	3	0	3	0	{3}	D 7 / D 4 A 2 = 64 * 7! / 8/4! / 2 = 280
A 4 A 1		1 20		5	dix	dix	0	5	*	1344	1	2	2	1	{} v ()	D 7 / A 4 A 1 = 64 * 7! / 5! / 2 = 1344
D 5 A 1		1 21	f 5	16	80	160	40	80	dix	16	84	*	2	0	{}	D 7 / D 5 A 1 = 64 * 7! / 16/5! / 2 = 84
A 5		1 30		6	15	20	0	15	0	6	*	448	1	1		D 7 / A 5 = 64 * 7! / 6! = 448
D 6		1 31	f 6	32	240	640	160	480	60	192	12	32	14	*	()	D 7 / D 6 = 64 * 7! / 32/6! = 14
A 6		1 40		7	21	35	0	35	0	21	0	7	*	64		D 7 / A 6 = 64 * 7! / 7! = 64

Polytopes associés

Il existe 95 polytopes uniformes avec une symétrie D ₆ , 63 sont partagés par la symétrie B ₆ et 32 ​​sont uniques:

Polytopes D7
t 0 (1 41 )	t 0,1 (1 41 )	t 0,2 (1 41 )	t 0,3 (1 41 )	t 0,4 (1 41 )	t 0,5 (1 41 )	t 0,1,2 (1 41 )	t 0,1,3 (1 41 )
t 0,1,4 (1 41 )	t 0,1,5 (1 41 )	t 0,2,3 (1 41 )	t 0,2,4 (1 41 )	t 0,2,5 (1 41 )	t 0,3,4 (1 41 )	t 0,3,5 (1 41 )	t 0,4,5 (1 41 )
t 0,1,2,3 (1 41 )	t 0,1,2,4 (1 41 )	t 0,1,2,5 (1 41 )	t 0,1,3,4 (1 41 )	t 0,1,3,5 (1 41 )	t 0,1,4,5 (1 41 )	t 0,2,3,4 (1 41 )	t 0,2,3,5 (1 41 )
t 0,2,4,5 (1 41 )	t 0,3,4,5 (1 41 )	t 0,1,2,3,4 (1 41 )	t 0,1,2,3,5 (1 41 )	t 0,1,2,4,5 (1 41 )	t 0,1,3,4,5 (1 41 )	t 0,2,3,4,5 (1 41 )	t 0,1,2,3,4,5 (1 41 )

Les références

• HSM Coxeter :
  • Coxeter, Regular Polytopes , (3e édition, 1973), édition Dover, ISBN  0-486-61480-8 , p. 296, Tableau I (iii): Polytopes réguliers, trois polytopes réguliers en n dimensions (n≥5)
  • HSM Coxeter, Regular Polytopes , 3e édition, Dover New York, 1973, p. 296, Tableau I (iii): Polytopes réguliers, trois polytopes réguliers en n dimensions (n≥5)
  • Kaleidoscopes: Selected Writings of HSM Coxeter , édité par F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN  978-0-471-01003-6 [1]
    • (Papier 22) HSM Coxeter, Polytopes réguliers et semi-réguliers I , [Math. Zeit. 46 (1940) 380-407, MR 2,10]
    • (Papier 23) HSM Coxeter, Polytopes II régulier et semi-régulier , [Math. Zeit. 188 (1985) 559-591]
    • (Papier 24) HSM Coxeter, Polytopes réguliers et semi-réguliers III , [Math. Zeit. 200 (1988) 3-45]
• John H.Conway, Heidi Burgiel, Chaim Goodman-Strass, Les symétries des choses 2008, ISBN  978-1-56881-220-5 (Chapitre 26. p. 409: Hemicubes: 1 _n1 )
• Klitzing, Richard. "Polytopes uniformes 7D (polyexa) x3o3o * b3o3o3o3o - hesa" .

Liens externes

• Olshevsky, George. "Demihepteract" . Glossaire de l'hyperespace . Archivé de l'original le 4 février 2007.
• Glossaire multidimensionnel