Théorème de Taylor - Taylor's theorem

La fonction exponentielle y  =  e ^x (rouge) et le polynôme de Taylor correspondant de degré quatre (vert tireté) autour de l'origine.

En calcul , le théorème de Taylor donne une approximation d'une fonction dérivable k fois autour d'un point donné par un polynôme de degré k , appelé polynôme de Taylor d' ordre k . Pour une fonction lisse , le polynôme de Taylor est la troncature à l'ordre k de la série de Taylor de la fonction. Le polynôme de Taylor de premier ordre est l' approximation linéaire de la fonction, et le polynôme de Taylor de second ordre est souvent appelé approximation quadratique . Il existe plusieurs versions du théorème de Taylor, certaines donnant des estimations explicites de l'erreur d'approximation de la fonction par son polynôme de Taylor.

Le théorème de Taylor porte le nom du mathématicien Brook Taylor , qui en a donné une version en 1715, bien qu'une version antérieure du résultat ait déjà été mentionnée en 1671 par James Gregory .

Le théorème de Taylor est enseigné dans les cours de calcul de niveau d'introduction et est l'un des outils élémentaires centraux de l' analyse mathématique . Il donne des formules arithmétiques simples pour calculer avec précision les valeurs de nombreuses fonctions transcendantales telles que la fonction exponentielle et les fonctions trigonométriques . C'est le point de départ de l'étude des fonctions analytiques , et est fondamental dans divers domaines des mathématiques, ainsi qu'en analyse numérique et en physique mathématique . Le théorème de Taylor se généralise également aux fonctions multivariées et vectorielles .

Motivation

Graphique de f ( x ) = e ^x (bleu) avec son approximation linéaire P ₁ ( x ) = 1 + x (rouge) à a  = 0.

Si une fonction à valeur réelle f ( x ) est dérivable au point x = a , alors elle a une approximation linéaire près de ce point. Cela signifie qu'il existe une fonction h ₁ ( x ) telle que

${\displaystyle f(x)=f(a)+f'(a)(xa)+h_{1}(x)(xa),\quad \lim _{x\to a}h_{1}(x )=0.}$

Ici

${\style d'affichage P_{1}(x)=f(a)+f'(a)(xa)}$

est l'approximation linéaire de f ( x ) pour x près du point a , dont le graphe y = P ₁ ( x ) est la tangente au graphe y = f ( x ) en x = a . L'erreur d'approximation est :

${\displaystyle R_{1}(x)=f(x)-P_{1}(x)=h_{1}(x)(xa).}$

Lorsque x tend vers  a, cette erreur atteint zéro beaucoup plus rapidement que , ce qui constitue une approximation utile. ${\style d'affichage f'(a)(x{-}a)}$${\style d'affichage f(x)\environ P_{1}(x)}$

Graphique de f ( x ) = e ^x (bleu) avec son approximation quadratique P ₂ ( x ) = 1 + x + x ² /2 (rouge) à a  = 0. Notez l'amélioration de l'approximation.

Pour une meilleure approximation de f ( x ), nous pouvons ajuster un polynôme quadratique au lieu d'une fonction linéaire :

${\displaystyle P_{2}(x)=f(a)+f'(a)(xa)+{\frac {f''(a)}{2}}(xa)^{2}.}$

Au lieu de simplement faire correspondre une dérivée de f ( x ) à x = a , ce polynôme a les mêmes première et seconde dérivées, comme cela est évident lors de la différenciation.

Le théorème de Taylor garantit que l' approximation quadratique est, dans un voisinage suffisamment petit de x = a , plus précise que l'approximation linéaire. Spécifiquement,

${\displaystyle f(x)=P_{2}(x)+h_{2}(x)(xa)^{2},\quad \lim _{x\to a}h_{2}(x)= 0.}$

Ici, l'erreur d'approximation est

${\style d'affichage R_{2}(x)=f(x)-P_{2}(x)=h_{2}(x)(xa)^{2},}$

qui, étant donné le comportement limite de , tend vers zéro plus rapidement que lorsque x tend vers  a . ${\style d'affichage h_{2}}$${\style d'affichage (xa)^{2}}$

Approximation de f ( x ) = 1/(1 +  x ² ) (bleu) par ses polynômes de Taylor P _k d'ordre k  = 1, …, 16 centrés en x  = 0 (rouge) et x  = 1 (vert). Les approximations ne s'améliorent pas du tout en dehors de (−1, 1) et (1 − √2, 1 + √2) respectivement.

De même, nous pourrions obtenir de meilleures approximations de f si nous utilisons des polynômes de degré supérieur, car nous pouvons alors faire correspondre encore plus de dérivées avec f au point de base sélectionné.

En général, l'erreur d'approximation d'une fonction par un polynôme de degré k ira vers zéro beaucoup plus rapidement que lorsque x tend vers  a . Cependant, il existe des fonctions, même infiniment dérivables, pour lesquelles augmenter le degré du polynôme d'approximation n'augmente pas la précision de l'approximation : on dit qu'une telle fonction n'est pas analytique en x = a : elle n'est pas (localement) déterminée par ses dérivés à ce stade. ${\style d'affichage (xa)^{k}}$

Le théorème de Taylor est de la nature asymptotique: elle nous indique seulement que l'erreur R _k dans une approximation par un k ordre de Taylor polynôme P _k tend vers zéro plus vite que tout non nul k -ème degré polynôme comme x  →  a . Il ne nous dit pas quelle est l'importance de l'erreur dans un voisinage concret du centre d'expansion, mais à cette fin, il existe des formules explicites pour le terme restant (données ci-dessous) qui sont valables sous certaines hypothèses de régularité supplémentaires sur f . Ces versions améliorées du théorème de Taylor conduisent généralement à des estimations uniformes de l'erreur d'approximation dans un petit voisinage du centre d'expansion, mais les estimations ne sont pas nécessairement valables pour des voisinages trop grands, même si la fonction f est analytique . Dans cette situation, il peut être nécessaire de sélectionner plusieurs polynômes de Taylor avec différents centres d'expansion pour avoir des approximations de Taylor fiables de la fonction d'origine (voir l'animation à droite.)

Il y a plusieurs façons d'utiliser le terme de reste :

1. Estimer l'erreur pour un polynôme P _k ( x ) de degré k estimant f ( x ) sur un intervalle donné ( a – r , a + r ). (Compte tenu de l'intervalle et du degré, nous trouvons l'erreur.)
2. Trouver le plus petit degré k pour lequel le polynôme P _k ( x ) se rapproche de f ( x ) à une tolérance d' erreur donnée sur un intervalle donné ( a − r , a + r ) . (Compte tenu de l'intervalle et de la tolérance d'erreur, nous trouvons le degré.)
3. Trouvez le plus grand intervalle ( a − r , a + r ) sur lequel P _k ( x ) se rapproche de f ( x ) avec une tolérance d'erreur donnée. (Compte tenu du degré et de la tolérance d'erreur, nous trouvons l'intervalle.)

Le théorème de Taylor en une variable réelle

Énoncé du théorème

L'énoncé précis de la version la plus basique du théorème de Taylor est le suivant :

Le polynôme apparaissant dans le théorème de Taylor est le polynôme de Taylor d'ordre k

${\displaystyle P_{k}(x)=f(a)+f'(a)(xa)+{\frac {f''(a)}{2!}}(xa)^{2}+\ cdots +{\frac {f^{(k)}(a)}{k!}}(xa)^{k}}$

de la fonction f au point a . Le polynôme de Taylor est l'unique polynôme "asymptotique le mieux ajusté" dans le sens où s'il existe une fonction h _k  : R → R et un polynôme d'ordre k p tel que

${\displaystyle f(x)=p(x)+h_{k}(x)(xa)^{k},\quad \lim _{x\to a}h_{k}(x)=0,}$

alors p  =  P _k . Le théorème de Taylor décrit le comportement asymptotique du terme restant

${\style d'affichage R_{k}(x)=f(x)-P_{k}(x),}$

qui est l' erreur d'approximation lors de l'approximation de f avec son polynôme de Taylor. En utilisant la notation little-o , l'énoncé du théorème de Taylor se lit comme suit

${\displaystyle R_{k}(x)=o(|xa|^{k}),\quad x\to a.}$

Formules explicites pour le reste

Sous des hypothèses de régularité plus fortes sur f, il existe plusieurs formules précises pour le terme de reste R _k du polynôme de Taylor, les plus courantes étant les suivantes.

Ces raffinements du théorème de Taylor sont généralement prouvés en utilisant le théorème de la valeur moyenne , d'où le nom. D'autres expressions similaires peuvent également être trouvées. Par exemple, si G ( t ) est continue sur l'intervalle fermé et dérivable par une dérivée non nulle sur l'intervalle ouvert entre a et x , alors

${\displaystyle R_{k}(x)={\frac {f^{(k+1)}(\xi )}{k!}}(x-\xi )^{k}{\frac {G( x)-G(a)}{G'(\xi )}}}$

pour un certain nombre ξ entre un et x . Cette version couvre les formes de Lagrange et de Cauchy du reste en tant que cas particuliers, et est prouvée ci-dessous en utilisant le théorème de la valeur moyenne de Cauchy .

L'énoncé de la forme intégrale du reste est plus avancé que les précédents, et nécessite une compréhension de la théorie de l' intégration de Lebesgue pour la pleine généralité. Cependant, cela vaut aussi dans le sens de l' intégrale de Riemann à condition que la ( k  + 1)ème dérivée de f soit continue sur l'intervalle fermé [ a , x ].

En raison de la continuité absolue de f ^{( k )} sur l' intervalle fermé entre a et x , sa dérivée f ^{( k +1)} existe en tant que fonction L ¹ , et le résultat peut être prouvé par un calcul formel utilisant le théorème fondamental du calcul et intégration par parties .

Estimations pour le reste

Il est souvent utile en pratique de pouvoir estimer le terme restant apparaissant dans l'approximation de Taylor, plutôt que d'avoir une formule exacte pour cela. Supposons que f soit ( k + 1) -fois continûment dérivable dans un intervalle I contenant a . Supposons qu'il existe des constantes réelles q et Q telles que

${\displaystyle q\leq f^{(k+1)}(x)\leq Q}$

tout au long de I . Alors le terme restant satisfait l'inégalité

${\displaystyle q{\frac {(xa)^{k+1}}{(k+1)!}}\leq R_{k}(x)\leq Q{\frac {(xa)^{k+ 1}}{(k+1) !}},}$

si x > a , et une estimation similaire si x < a . C'est une simple conséquence de la forme de Lagrange du reste. En particulier, si

${\displaystyle |f^{(k+1)}(x)|\leq M}$

sur un intervalle I = ( a − r , a + r ) avec certains , alors ${\style d'affichage r>0}$

${\displaystyle |R_{k}(x)|\leq M{\frac {|xa|^{k+1}}{(k+1)!}}\leq M{\frac {r^{k+ 1}}{(k+1)!}}}$

pour tout x ∈( a − r , a + r ). La deuxième inégalité est appelée une estimation uniforme , car elle est valable uniformément pour tout x sur l'intervalle ( a − r , a + r ).

Exemple

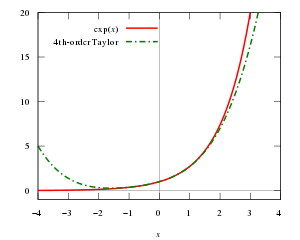
Approximation de e ^x (bleu) par ses polynômes de Taylor P _k d'ordre k  = 1,…,7 centrés en x  = 0 (rouge).

Supposons que l'on souhaite trouver la valeur approchée de la fonction f ( x ) = e ^x sur l'intervalle [−1,1] en s'assurant que l'erreur d'approximation n'est pas supérieure à 10 ⁻⁵ . Dans cet exemple, nous prétendons que nous ne connaissons que les propriétés suivantes de la fonction exponentielle :

${\displaystyle e^{0}=1,\qquad {\frac {d}{dx}}e^{x}=e^{x},\qquad e^{x}>0,\qquad x\in \mathbb {R} .}$

( ⁎ )

De ces propriétés il résulte que f ^{( k )} ( x ) = e ^x pour tout k , et en particulier, f ^{( k )} (0) = 1 . Par conséquent, le polynôme de Taylor d'ordre k de f à 0 et son terme de reste sous la forme de Lagrange sont donnés par

${\displaystyle P_{k}(x)=1+x+{\frac {x^{2}}{2!}}+\cdots +{\frac {x^{k}}{k!}},\ qquad R_{k}(x)={\frac {e^{\xi }}{(k+1)!}}x^{k+1},}$

où ξ est un nombre entre 0 et x . Puisque e ^x augmente de ( ⁎ ), nous pouvons simplement utiliser e ^x  ≤ 1 pour x  ∈ [−1, 0] pour estimer le reste sur le sous-intervalle [−1, 0]. Pour obtenir une majoration du reste sur [0,1], on utilise la propriété e ^ξ < e ^x pour 0< ξ < x pour estimer

${\displaystyle e^{x}=1+x+{\frac {e^{\xi }}{2}}x^{2}<1+x+{\frac {e^{x}}{2}} x^{2},\qquad 0<x\leq 1}$

en utilisant le développement de Taylor du second ordre. Ensuite, nous résolvons pour e ^x pour en déduire que

${\displaystyle e^{x}\leq {\frac {1+x}{1-{\frac {x^{2}}{2}}}}=2{\frac {1+x}{2- x^{2}}}\leq 4,\qquad 0\leq x\leq 1}$

simplement en maximisant le numérateur et en minimisant le dénominateur . En combinant ces estimations pour e ^x, nous voyons que

${\displaystyle |R_{k}(x)|\leq {\frac {4|x|^{k+1}}{(k+1)!}}\leq {\frac {4}{(k+ 1)!}},\qquad -1\leq x\leq 1,}$

la précision requise est donc certainement atteinte, lorsque

${\displaystyle {\frac {4}{(k+1)!}}<10^{-5}\quad \Longleftrightarrow \quad 4\cdot 10^{5}<(k+1)!\quad \Longleftrightarrow \quad k\geq 9.}$

(Voir factorielle ou calculer à la main les valeurs 9 ! =362 880 et 10 ! =3 628 800 .) En conclusion, le théorème de Taylor conduit à l'approximation

${\displaystyle e^{x}=1+x+{\frac {x^{2}}{2!}}+\cdots +{\frac {x^{9}}{9!}}+R_{9 }(x),\qquad |R_{9}(x)|<10^{-5},\qquad -1\leq x\leq 1.}$

Par exemple, cette approximation fournit une expression décimale e  2,71828, correcte jusqu'à cinq décimales.

Relation à l'analyticité

Développements de Taylor de fonctions analytiques réelles

Soit I ⊂ R un intervalle ouvert . Par définition, une fonction f  : I → R est réelle analytique si elle est définie localement par une série convergente . Cela signifie que pour chaque a  ∈  I il existe un r  > 0 et une séquence de coefficients c _k  ∈  R tel que ( a - r , a + r ) ⊂ I et

${\displaystyle f(x)=\sum _{k=0}^{\infty }c_{k}(xa)^{k}=c_{0}+c_{1}(xa)+c_{2} (xa)^{2}+\cdots ,\qquad |xa|<r.}$

En général, le rayon de convergence d'une série entière peut être calculé à partir de la formule de Cauchy-Hadamard

${\displaystyle {\frac {1}{R}}=\limsup _{k\to \infty }|c_{k}|^{\frac {1}{k}}.}$

Ce résultat est basé sur la comparaison avec une série géométrique et les mêmes émissions de procédé que si les séries de puissance basé sur un converge pour un certain b ∈ R , il doit converger uniformément sur l' intervalle fermé [ a - r _b , a + r _b ] , où r _b  = | b  −  un |. Ici, seule la convergence des séries entières est considérée, et il se pourrait bien que ( a − R , a + R ) s'étende au-delà du domaine I de f .

Les polynômes de Taylor de la fonction analytique réelle f en a sont simplement les troncatures finies

${\displaystyle P_{k}(x)=\sum _{j=0}^{k}c_{j}(xa)^{j},\qquad c_{j}={\frac {f^{( j)}(a)}{j!}}}$

de sa série de puissances définissant localement, et les termes restants correspondants sont donnés localement par les fonctions analytiques

${\displaystyle R_{k}(x)=\sum _{j=k+1}^{\infty }c_{j}(xa)^{j}=(xa)^{k}h_{k}( x),\qquad |xa|<r.}$

Ici les fonctions

${\displaystyle {\begin{aligned}&h_{k}:(ar,a+r)\to \mathbb {R} \\&h_{k}(x)=(xa)\sum _{j=0}^ {\infty }c_{k+1+j}\left(xa\right)^{j}\end{aligned}}}$

sont également analytiques, puisque leurs séries de puissances définissantes ont le même rayon de convergence que la série originale. En supposant que [ a - r , a + r ] ⊂ I et r  <  R , toutes ces séries convergent uniformément sur ( a - r , a + r ) . Naturellement, dans le cas des fonctions analytiques, on peut estimer le terme de reste R _k ( x ) par la queue de la séquence des dérivées f′ ( a ) au centre du développement, mais en utilisant l' analyse complexe aussi une autre possibilité se présente, qui est décrit ci - dessous .

Théorème de Taylor et convergence des séries de Taylor

La série de Taylor de f convergera dans un intervalle dans lequel toutes ses dérivées sont bornées et ne croissent pas trop vite lorsque k tend vers l'infini. (Cependant, même si la série de Taylor converge, elle pourrait ne pas converger vers f , comme expliqué ci-dessous ; f est alors dit non analytique .)

On pourrait penser à la série Taylor

${\displaystyle f(x)\approx \sum _{k=0}^{\infty }c_{k}(xa)^{k}=c_{0}+c_{1}(xa)+c_{2 }(xa)^{2}+\cdots }$

d'une fonction dérivable à l'infini f  : R → R comme son « polynôme de Taylor d'ordre infini » en a . Maintenant, les estimations pour le reste impliquent que si, pour tout r , les dérivées de f sont connues pour être bornées ( a  −  r , a  +  r ), alors pour tout ordre k et pour tout r  > 0 il existe une constante M _k,r > 0 tel que

${\displaystyle |R_{k}(x)|\leq M_{k,r}{\frac {|xa|^{k+1}}{(k+1)!}}}$

( ⁎⁎ )

pour tout x  ∈ ( a  −  r , a  +  r ). Parfois, les constantes M _k,r peuvent être choisies de telle sorte que M _k,r soit majoré au-dessus, pour r fixe et tout k . Alors la série de Taylor de f converge uniformément vers une fonction analytique

${\displaystyle {\begin{aligned}&T_{f}:(ar,a+r)\to \mathbb {R} \\&T_{f}(x)=\sum _{k=0}^{\infty }{\frac {f^{(k)}(a)}{k!}}\left(xa\right)^{k}\end{aligned}}}$

(On obtient également la convergence même si M _k,r n'est pas borné au-dessus tant qu'il croît assez lentement.)

La fonction limite T _f est par définition toujours analytique, mais elle n'est pas nécessairement égale à la fonction d'origine f , même si f est infiniment dérivable. Dans ce cas, on dit que f est une fonction lisse non analytique , par exemple une fonction plate :

${\displaystyle {\begin{aligned}&f:\mathbb {R} \to \mathbb {R} \\&f(x)={\begin{cases}e^{-{\frac {1}{x^{ 2}}}}&x>0\\0&x\leq 0.\end{cas}}\end{aligned}}}$

En utilisant la règle de la chaîne à plusieurs reprises par induction mathématique , on montre que pour tout ordre  k ,

${\displaystyle f^{(k)}(x)={\begin{cases}{\frac {p_{k}(x)}{x^{3k}}}\cdot e^{-{\frac { 1}{x^{2}}}}&x>0\\0&x\leq 0\end{cas}}}$

pour un polynôme p _k de degré 2( k − 1). La fonction tend vers zéro plus rapidement que n'importe quel polynôme lorsque x → 0 , donc f est infiniment dérivable et f ^{( k )} (0) = 0 pour chaque entier positif k . Les résultats ci-dessus sont tous valables dans ce cas : ${\displaystyle e^{-{\frac {1}{x^{2}}}}}$

• La série de Taylor de f converge uniformément vers la fonction nulle T _f ( x ) = 0, qui est analytique avec tous les coefficients égaux à zéro.
• La fonction f est inégale à cette série de Taylor, et donc non analytique.
• Pour toute commande k  ∈  N et de rayon r  > 0 , il existe M _{k, r}  > 0 satisfaisant le reste lié ( ⁎⁎ ) ci - dessus.

Cependant, comme k augmente pour fixe r , la valeur de M _{k, r} croît plus rapidement que r ^k , et l'erreur ne va pas à zéro .

Le théorème de Taylor en analyse complexe

Théorème de Taylor se généralise à des fonctions f  : C → C qui sont complexes différentiable dans une partie ouverte U  ⊂  C du plan complexe . Cependant, son utilité est éclipsée par d'autres théorèmes généraux en analyse complexe . À savoir, des versions plus fortes des résultats connexes peuvent être déduites pour les fonctions dérivables complexes f  :  U  →  C en utilisant la formule intégrale de Cauchy comme suit.

Soit r  > 0 tel que le disque fermé B ( z ,  r )  S ( z ,  r ) soit contenu dans U . Alors la formule intégrale de Cauchy de paramétrisation positive γ ( t ) = z + re ^it du cercle S ( z , r ) avec t [0, 2 π ] donne

${\displaystyle f(z)={\frac {1}{2\pi i}}\int _{\gamma }{\frac {f(w)}{wz}}\,dw,\quad f'( z)={\frac {1}{2\pi i}}\int _{\gamma }{\frac {f(w)}{(wz)^{2}}}\,dw,\quad \ldots ,\quad f^{(k)}(z)={\frac {k!}{2\pi i}}\int _{\gamma }{\frac {f(w)}{(wz)^{ k+1}}}\,dw.}$

Ici tous les intégrandes sont continus sur le cercle S ( z ,  r ), ce qui justifie la différenciation sous le signe intégral. En particulier, si f est une fois complexe dérivable sur l'ouvert U , alors il est en fait infiniment dérivable complexe sur U . On obtient aussi les estimations de Cauchy

${\displaystyle |f^{(k)}(z)|\leq {\frac {k!}{2\pi }}\int _{\gamma }{\frac {M_{r}}{|wz| ^{k+1}}}\,dw={\frac {k!M_{r}}{r^{k}}},\quad M_{r}=\max _{|wc|=r}| f(w)|}$

pour tout z  ∈  U et r  > 0 tel que B ( z ,  r ) ∪  S ( c ,  r )  U . Ces estimations impliquent que la série complexe de Taylor

${\displaystyle T_{f}(z)=\sum _{k=0}^{\infty }{\frac {f^{(k)}(c)}{k!}}(zc)^{k }}$

of f converge uniformément sur tout disque ouvert B ( c ,  r )  U avec S ( c ,  r ) ⊂  U vers une fonction T _f . De plus, en utilisant les formules intégrales de contour pour les dérivées f ^{( k )} ( c ),

${\displaystyle {\begin{aligned}T_{f}(z)&=\sum _{k=0}^{\infty }{\frac {(zc)^{k}}{2\pi i}} \int _{\gamma }{\frac {f(w)}{(wc)^{k+1}}}\,dw\\&={\frac {1}{2\pi i}}\int _{\gamma }{\frac {f(w)}{wc}}\sum _{k=0}^{\infty }\left({\frac {zc}{wc}}\right)^{k }\,dw\\&={\frac {1}{2\pi i}}\int _{\gamma }{\frac {f(w)}{wc}}\left({\frac {1} {1-{\frac {zc}{wc}}}}\right)\,dw\\&={\frac {1}{2\pi i}}\int _{\gamma }{\frac {f (w)}{wz}}\,dw=f(z),\end{aligné}}}$

de sorte que toute différentiable complexe fonction f dans un ensemble ouvert U  ⊂  C est en fait analytique complexe . Tout ce qui est dit pour les fonctions analytiques réelles ici tient également des fonctions analytiques complexes avec l'intervalle ouvert I remplacé par un sous - ensemble ouvert U  ∈  C et un intervalle -centered ( a  -  r ,  un  +  r ) est remplacé par c -centered disques B ( c ,  r ). En particulier, le développement de Taylor se présente sous la forme

${\displaystyle f(z)=P_{k}(z)+R_{k}(z),\quad P_{k}(z)=\sum _{j=0}^{k}{\frac { f^{(j)}(c)}{j!}}(zc)^{j},}$

où le terme restant R _k est analytique complexe. Les méthodes d'analyse complexe fournissent des résultats puissants concernant les développements de Taylor. Par exemple, en utilisant la formule intégrale de Cauchy pour tout orienté positivement courbe de Jordan γ qui paramétrise la limite ∂ W  ⊂  U d'une région W  ⊂  U , on obtient des expressions pour les dérivés f ^{( j )} ( c ) comme ci - dessus, et en modifiant légèrement le calcul pour T _f ( z ) = f ( z ) , on arrive à la formule exacte

${\displaystyle R_{k}(z)=\sum _{j=k+1}^{\infty }{\frac {(zc)^{j}}{2\pi i}}\int _{\ gamma }{\frac {f(w)}{(wc)^{j+1}}}\,dw={\frac {(zc)^{k+1}}{2\pi i}}\int _{\gamma }{\frac {f(w)\,dw}{(wc)^{k+1}(wz)}},\qquad z\in W.}$

La caractéristique importante est que la qualité de l'approximation par un polynôme de Taylor sur la région W  ⊂  U est dominé par les valeurs de la fonction f lui-même sur la frontière ∂ W  ⊂  U . De même, en appliquant les estimations de Cauchy à l'expression de la série pour le reste, on obtient les estimations uniformes

${\displaystyle |R_{k}(z)|\leq \sum _{j=k+1}^{\infty }{\frac {M_{r}|zc|^{j}}{r^{j }}}={\frac {M_{r}}{r^{k+1}}}{\frac {|zc|^{k+1}}{1-{\frac {|zc|}{r }}}}\leq {\frac {M_{r}\beta ^{k+1}}{1-\beta }},\qquad {\frac {|zc|}{r}}\leq \beta < 1.}$

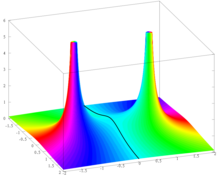
Exemple

Tracé complexe de f ( z ) = 1/(1 +  z ² ). Modulus est représenté par l' élévation et l' argument en colorant cyan = 0, bleu =  π / 3, violet = 2 π / 3, rouge =  tc , jaune = 4 π / 3, vert = 5 π / 3.

La fonction

${\displaystyle {\begin{aligned}&f:\mathbb {R} \to \mathbb {R} \\&f(x)={\frac {1}{1+x^{2}}}\end{aligned }}}$

est réelle analytique , c'est-à-dire localement déterminée par sa série de Taylor. Cette fonction a été tracée ci-dessus pour illustrer le fait que certaines fonctions élémentaires ne peuvent pas être approchées par des polynômes de Taylor dans les voisinages du centre d'expansion qui sont trop grands. Ce type de comportement se comprend aisément dans le cadre d'analyses complexes. A savoir, la fonction f s'étend en une fonction méromorphe

${\displaystyle {\begin{aligned}&f:\mathbb {C} \cup \{\infty \}\to \mathbb {C} \cup \{\infty \}\\&f(z)={\frac { 1}{1+z^{2}}}\end{aligned}}}$

sur le plan complexe compacté. Elle a des pôles simples en z  =  i et z  = − i , et elle est analytique ailleurs. Or sa série de Taylor centrée en z ₀ converge sur tout disque B ( z ₀ , r ) avec r < | z  -  z ₀ |, où les mêmes converge série Taylor à z  ∈  C . Par conséquent, la série de Taylor de f centrée en 0 converge vers B (0, 1) et elle ne converge pas pour tout z ∈ C avec | z | > 1 dû aux pôles en i et − i . Pour la même raison , la série de Taylor de f centrée à 1 converge sur B (1, √2) et ne converge pas pour tout z  ∈  C avec | z  − 1| > 2.

Généralisations du théorème de Taylor

Différenciation d'ordre supérieur

Une fonction f : R ⁿ  →  R est dérivable en a  ∈  R ⁿ si et seulement s'il existe une fonctionnelle linéaire L  :  R ⁿ  →  R et une fonction h  :  R ⁿ  →  R telles que

${\displaystyle f({\boldsymbol {x}})=f({\boldsymbol {a}})+L({\boldsymbol {x}}-{\boldsymbol {a}})+h({\boldsymbol { x}})\lVert {\boldsymbol {x}}-{\boldsymbol {a}}\rVert ,\qquad \lim _{{\boldsymbol {x}}\to {\boldsymbol {a}}}h({ \boldsymbol {x}})=0.}$

Si tel est le cas, alors L  =  df ( a ) est le (définie de manière unique) différentiel de f au point a . De plus, alors les dérivées partielles de f existent en a et la différentielle de f en a est donnée par

${\displaystyle df({\boldsymbol {a}})({\boldsymbol {v}})={\frac {\partial f}{\partial x_{1}}}({\boldsymbol {a}})v_ {1}+\cdots +{\frac {\partial f}{\partial x_{n}}}({\boldsymbol {a}})v_{n}.}$

Introduire la notation multi-index

${\displaystyle |\alpha |=\alpha _{1}+\cdots +\alpha _{n},\quad \alpha !=\alpha _{1}!\cdots \alpha _{n}!,\quad {\boldsymbol {x}}^{\alpha }=x_{1}^{\alpha _{1}}\cdots x_{n}^{\alpha _{n}}}$

pour α  ∈  N ⁿ et x  ∈  R ⁿ . Si toutes les dérivées partielles d' ordre k de f  : R ⁿ → R sont continues en a ∈ R ⁿ , alors par le théorème de Clairaut , on peut changer l'ordre des dérivées mixtes en a , donc la notation

${\displaystyle D^{\alpha }f={\frac {\partial ^{|\alpha |}f}{\partial x_{1}^{\alpha _{1}}\cdots \partial x_{n} ^{\alpha _{n}}}},\qquad |\alpha |\leq k}$

pour les dérivées partielles d' ordre supérieur est justifiée dans cette situation. Il en est de même si toutes les  dérivées partielles ( k − 1)-ième ordre de f existent dans un voisinage de a et sont dérivables en a . On dit alors que f est k fois dérivable au point  a .

Théorème de Taylor pour les fonctions multivariées

Si la fonction f  : R ⁿ → R est k  + 1 fois continûment dérivable dans une boule fermée pour certains , alors on peut dériver une formule exacte pour le reste en termes de ( k + 1) dérivées partielles d' ordre de f dans ce quartier. À savoir, ${\displaystyle B=\{\mathbf {y} \in \mathbb {R} ^{n}:\left\|\mathbf {a} -\mathbf {y} \right\|\leq r\}}$${\style d'affichage r>0}$

${\displaystyle {\begin{aligned}&f({\boldsymbol {x}})=\sum _{|\alpha |\leq k}{\frac {D^{\alpha }f({\boldsymbol {a} })}{\alpha !}}({\boldsymbol {x}}-{\boldsymbol {a}})^{\alpha }+\sum _{|\beta |=k+1}R_{\beta } ({\boldsymbol {x}})({\boldsymbol {x}}-{\boldsymbol {a}})^{\beta },\\&R_{\beta }({\boldsymbol {x}})={ \frac {|\beta |}{\beta !}}\int _{0}^{1}(1-t)^{|\beta |-1}D^{\beta }f{\big (} {\boldsymbol {a}}+t({\boldsymbol {x}}-{\boldsymbol {a}}){\big )}\,dt.\end{aligned}}}$

Dans ce cas, en raison de la continuité des dérivées partielles ( k + 1)-ième ordre dans l' ensemble compact B , on obtient immédiatement les estimations uniformes

${\displaystyle \left|R_{\beta }({\boldsymbol {x}})\right|\leq {\frac {1}{\beta !}}\max _{|\alpha |=|\beta | }\max _{{\boldsymbol {y}}\in B}|D^{\alpha }f({\boldsymbol {y}})|,\qquad {\boldsymbol {x}}\in B.}$

Exemple en deux dimensions

Par exemple, le polynôme de Taylor du troisième ordre d'une fonction lisse f : R ²  →  R est, dénotant x − a = v ,

${\displaystyle {\begin{aligned}P_{3}({\boldsymbol {x}})=f({\boldsymbol {a}})+{}&{\frac {\partial f}{\partial x_{ 1}}}({\boldsymbol {a}})v_{1}+{\frac {\partial f}{\partial x_{2}}}({\boldsymbol {a}})v_{2}+{ \frac {\partial ^{2}f}{\partial x_{1}^{2}}}({\boldsymbol {a}}){\frac {v_{1}^{2}}{2 !} }+{\frac {\partial ^{2}f}{\partial x_{1}\partial x_{2}}}({\boldsymbol {a}})v_{1}v_{2}+{\frac {\partial ^{2}f}{\partial x_{2}^{2}}}({\boldsymbol {a}}){\frac {v_{2}^{2}}{2 !}}\ \&+{\frac {\partial ^{3}f}{\partial x_{1}^{3}}}({\boldsymbol {a}}){\frac {v_{1}^{3}} {3!}}+{\frac {\partial ^{3}f}{\partial x_{1}^{2}\partial x_{2}}}({\boldsymbol {a}}){\frac { v_{1}^{2}v_{2}}{2 !}}+{\frac {\partial ^{3}f}{\partial x_{1}\partial x_{2}^{2}}} ({\boldsymbol {a}}){\frac {v_{1}v_{2}^{2}}{2 !}}+{\frac {\partial ^{3}f}{\partial x_{2 }^{3}}}({\boldsymbol {a}}){\frac {v_{2}^{3}}{3!}}\end{aligned}}}$

Preuves

Preuve du théorème de Taylor en une variable réelle

Laisser

${\displaystyle h_{k}(x)={\begin{cases}{\frac {f(x)-P(x)}{(xa)^{k}}}&x\not =a\\0&x= a\fin{cas}}}$

où, comme dans l'énoncé du théorème de Taylor,

${\displaystyle P(x)=f(a)+f'(a)(xa)+{\frac {f''(a)}{2!}}(xa)^{2}+\cdots +{ \frac {f^{(k)}(a)}{k!}}(xa)^{k}.}$

Il suffit de montrer que

${\displaystyle \lim _{x\to a}h_{k}(x)=0.}$

La preuve ici est basée sur l'application répétée de la règle de L'Hôpital . Notons que, pour chaque j = 0,1,…, k −1 , . Donc chacune des k- 1 premières dérivées du numérateur en s'annule en , et il en est de même du dénominateur. Aussi, puisque la condition que la fonction f soit k fois dérivable en un point requiert une différentiabilité jusqu'à l'ordre k -1 dans un voisinage dudit point (cela est vrai, car la différentiabilité nécessite qu'une fonction soit définie dans tout un voisinage d'un point ), le numérateur et ses k  − 2 dérivées sont dérivables au voisinage de a . De toute évidence, le dénominateur satisfait également ladite condition, et en plus, ne disparaît pas à moins que x = a , donc toutes les conditions nécessaires à la règle de L'Hôpital sont remplies, et son utilisation est justifiée. Donc ${\style d'affichage f^{(j)}(a)=P^{(j)}(a)}$${\style d'affichage h_{k}(x)}$${\style d'affichage x=a}$

${\displaystyle {\begin{aligned}\lim _{x\to a}{\frac {f(x)-P(x)}{(xa)^{k}}}&=\lim _{x\ à a}{\frac {{\frac {d}{dx}}(f(x)-P(x))}{{\frac {d}{dx}}(xa)^{k}}}= \cdots =\lim _{x\to a}{\frac {{\frac {d^{k-1}}{dx^{k-1}}}(f(x)-P(x))} {{\frac {d^{k-1}}{dx^{k-1}}}(xa)^{k}}}\\&={\frac {1}{k!}}\lim _ {x\à un}{\frac {f^{(k-1)}(x)-P^{(k-1)}(x)}{xa}}\\&={\frac {1} {k!}}(f^{(k)}(a)-f^{(k)}(a))=0\end{aligned}}}$

où la dernière égalité suit par la définition de la dérivée à  x  =  a .

Dérivation pour les formes de valeur moyenne du reste

Soit G une fonction à valeur réelle, continue sur l'intervalle fermé entre a et x et dérivable avec une dérivée non nulle sur l'intervalle ouvert entre a et x , et définissons

${\displaystyle F(t)=f(t)+f'(t)(xt)+{\frac {f''(t)}{2!}}(xt)^{2}+\cdots +{ \frac {f^{(k)}(t)}{k!}}(xt)^{k}.}$

Pour . Alors, par le théorème de la valeur moyenne de Cauchy , ${\style d'affichage t\in [a,x]}$

${\displaystyle {\frac {F'(\xi )}{G'(\xi )}}={\frac {F(x)-F(a)}{G(x)-G(a)}} }$

( ⁎⁎⁎ )

pour un certain sur l'intervalle ouvert entre a et x . Notez qu'ici le numérateur F ( x ) − F ( a ) = R _k ( x ) est exactement le reste du polynôme de Taylor pour f ( x ). Calculer

${\displaystyle {\begin{aligned}F'(t)={}&f'(t)+{\big (}f''(t)(xt)-f'(t){\big )}+\ gauche({\frac {f^{(3)}(t)}{2!}}(xt)^{2}-{\frac {f^{(2)}(t)}{1!}} (xt)\right)+\cdots \\&\cdots +\left({\frac {f^{(k+1)}(t)}{k!}}(xt)^{k}-{\ frac {f^{(k)}(t)}{(k-1)!}}(xt)^{k-1}\right)={\frac {f^{(k+1)}(t )}{k!}}(xt)^{k},\end{aligned}}}$

branchez-le sur ( ⁎⁎⁎ ) et réorganisez les termes pour trouver que

${\displaystyle R_{k}(x)={\frac {f^{(k+1)}(\xi )}{k!}}(x-\xi )^{k}{\frac {G( x)-G(a)}{G'(\xi )}}.}$

C'est la forme du terme de reste mentionné après l'énoncé réel du théorème de Taylor avec reste sous la forme de la valeur moyenne. La forme Lagrange du reste se trouve en choisissant et la forme Cauchy en choisissant . ${\style d'affichage G(t)=(xt)^{k+1}}$${\style d'affichage G(t)=ta}$

Remarque. En utilisant cette méthode on peut aussi récupérer la forme intégrale du reste en choisissant

${\displaystyle G(t)=\int _{a}^{t}{\frac {f^{(k+1)}(s)}{k!}}(xs)^{k}\,ds ,}$

mais les exigences pour f nécessaires à l'utilisation du théorème de la valeur moyenne sont trop fortes, si l'on cherche à prouver l'affirmation dans le cas où f ^{( k )} n'est qu'absolument continue . Cependant, si l'on utilise l' intégrale de Riemann au lieu de l' intégrale de Lebesgue , les hypothèses ne peuvent pas être affaiblies.

Dérivation de la forme intégrale du reste

En raison de la continuité absolue de f ^{( k )} sur l' intervalle fermé entre a et x, sa dérivée f ^{( k +1)} existe en tant que fonction L ¹ , et nous pouvons utiliser le théorème fondamental du calcul et de l' intégration par parties . Cette même preuve s'applique pour l' intégrale de Riemann en supposant que f ^{( k )} est continue sur l'intervalle fermé et dérivable sur l' intervalle ouvert entre a et x , et cela conduit au même résultat qu'en utilisant le théorème de la valeur moyenne.

Le théorème fondamental du calcul dit que

${\displaystyle f(x)=f(a)+\int _{a}^{x}\,f'(t)\,dt.}$

Maintenant, nous pouvons intégrer par parties et utiliser à nouveau le théorème fondamental du calcul pour voir que

${\displaystyle {\begin{aligned}f(x)&=f(a)+{\Big (}xf'(x)-af'(a){\Big )}-\int _{a}^{ x}tf''(t)\,dt\\&=f(a)+x\left(f'(a)+\int _{a}^{x}f''(t)\,dt\ à droite)-af'(a)-\int _{a}^{x}tf''(t)\,dt\\&=f(a)+(xa)f'(a)+\int _{ a}^{x}\,(xt)f''(t)\,dt,\end{aligned}}}$

qui est exactement le théorème de Taylor avec reste sous forme intégrale dans le cas k =1. L'énoncé général est prouvé par induction . Supposer que

${\displaystyle f(x)=f(a)+{\frac {f'(a)}{1!}}(xa)+\cdots +{\frac {f^{(k)}(a)} {k!}}(xa)^{k}+\int _{a}^{x}{\frac {f^{(k+1)}(t)}{k!}}(xt)^{ k}\,dt.}$

( ⁎⁎⁎⁎ )

En intégrant le terme restant par parties, nous arrivons à

${\displaystyle {\begin{aligned}\int _{a}^{x}{\frac {f^{(k+1)}(t)}{k!}}(xt)^{k}\, dt=&-\left[{\frac {f^{(k+1)}(t)}{(k+1)k!}}(xt)^{k+1}\right]_{a} ^{x}+\int _{a}^{x}{\frac {f^{(k+2)}(t)}{(k+1)k!}}(xt)^{k+1 }\,dt\\=&\ {\frac {f^{(k+1)}(a)}{(k+1)!}}(xa)^{k+1}+\int _{a }^{x}{\frac {f^{(k+2)}(t)}{(k+1)!}}(xt)^{k+1}\,dt.\end{aligned}} }$

Dans la reportant cette formule dans ( ⁎⁎⁎⁎ ) montre que si elle est valable pour la valeur k , il faut aussi tenir la valeur k  + 1. Par conséquent, étant donné qu'il détient pour k  = 1, il faut tenir pour tout entier positif  k .

Dérivation pour le reste des polynômes de Taylor multivariés

On montre le cas particulier où f  : R ⁿ → R a des dérivées partielles continues jusqu'à l'ordre k +1 dans une boule fermée B de centre a . La stratégie de la démonstration consiste à appliquer le cas à une variable du théorème de Taylor à la restriction de f au segment de droite adjacent à x et a . Paramétrer le segment de droite entre a et x par u ( t ) = a + t ( x − a ). Nous appliquons la version à une variable du théorème de Taylor à la fonction g ( t ) = f ( u ( t )) :

${\displaystyle f(\mathbf {x} )=g(1)=g(0)+\sum _{j=1}^{k}{\frac {1}{j!}}g^{(j )}(0)\ +\ \int _{0}^{1}{\frac {(1-t)^{k}}{k!}}g^{(k+1)}(t)\ ,dt.}$

L'application de la règle de la chaîne pour plusieurs variables donne

${\displaystyle {\begin{aligned}g^{(j)}(t)&={\frac {d^{j}}{dt^{j}}}f(u(t))={\frac {d^{j}}{dt^{j}}}f(\mathbf {a} +t(\mathbf {x} -\mathbf {a} ))\\&=\sum _{|\alpha | =j}\gauche({\begin{matrice}j\\\alpha \end{matrice}}\right)(D^{\alpha }f)(\mathbf {a} +t(\mathbf {x} - \mathbf {a} ))(\mathbf {x} -\mathbf {a} )^{\alpha }\end{aligned}}}$

où est le coefficient multinomial . Depuis , on obtient : ${\displaystyle {\tbinom {j}{\alpha }}}$${\displaystyle {\tfrac {1}{j!}}{\tbinom {j}{\alpha }}={\tfrac {1}{\alpha !}}}$

${\displaystyle f(\mathbf {x} )=f(\mathbf {a} )+\sum _{1\leq |\alpha |\leq k}{\frac {1}{\alpha !}}(D ^{\alpha }f)(\mathbf {a} )(\mathbf {x} -\mathbf {a} )^{\alpha }+\sum _{|\alpha |=k+1}{\frac { k+1}{\alpha !}}(\mathbf {x} -\mathbf {a} )^{\alpha }\int _{0}^{1}(1-t)^{k}(D^ {\alpha }f)(\mathbf {a} +t(\mathbf {x} -\mathbf {a} ))\,dt.}$

Voir également

• Lemme d'Hadamard
• Série de Laurent  – Série de puissance généralisée pour permettre des puissances négatives
• Approximant de Padé  - "Meilleure" approximation d'une fonction par une fonction rationnelle d'ordre donné
• Série Newton

Notes de bas de page

Les références

• Apostol, Tom (1967), Tournesol , Wiley, ISBN 0-471-00005-1.
• Apostol, Tom (1974), Analyse mathématique , Addison-Wesley.
• Bartle, Robert G.; Sherbert, Donald R. (2011), Introduction à l'analyse réelle (4e éd.), Wiley, ISBN 978-0-471-43331-6.
• Hörmander, L. (1976), Opérateurs différentiels partiels linéaires, Volume 1 , Springer, ISBN 978-3-540-00662-6.
• Kline, Morris (1972), La pensée mathématique des temps anciens aux temps modernes, Volume 2 , Oxford University Press.
• Kline, Morris (1998), Calcul : une approche intuitive et physique , Douvres, ISBN 0-486-40453-6.
• Pedrick, George (1994), Un premier cours d'analyse , Springer, ISBN 0-387-94108-8.
• Stromberg, Karl (1981), Introduction à l'analyse réelle classique , Wadsworth, ISBN 978-0-534-98012-2.
• Rudin, Walter (1987), Analyse réelle et complexe (3e éd.), McGraw-Hill, ISBN 0-07-054234-1.
• Tao, Terence (2014), Analyse, Volume I (3e éd.), Hindustan Book Agency, ISBN 978-93-80250-64-9.

Liens externes

• Le théorème de Taylor sur ProofWiki
• Approximation de la série Taylor au cosinus à couper le nœud
• Applet démonstratif interactif d' expansion de Taylor trigonométrique
• La série Taylor revisitée au Holistic Numerical Methods Institute