Groupe en alternance - Alternating group
|
Structure algébrique → Théorie des groupes Théorie des groupes |
|---|
 |
En mathématiques , un groupe alterné est le groupe des permutations paires d'un ensemble fini . Le groupe alterné sur un ensemble de n éléments est appelé le groupe alterné de degré n , ou le groupe alterné sur n lettres et noté A n ou Alt ( n ).
Propriétés de base
Pour n > 1 , le groupe A n est le sous - groupe de commutateurs du groupe symétrique S n d' indice 2 et a donc n ! / 2 éléments. C'est le noyau du groupe de signature homomorphisme sgn: S n → {1, −1} expliqué sous groupe symétrique .
Le groupe A n est abélien si et seulement si n ≤ 3 et simple si et seulement si n = 3 ou n ≥ 5 . A 5 est le plus petit groupe simple non abélien , d'ordre 60, et le plus petit groupe non résoluble .
Le groupe A 4 a les quatre groupes de Klein V comme sous-groupe normal propre , à savoir l'identité et les doubles transpositions {(), (12) (34), (13) (24), (14) (23)} , c'est le noyau de la surjection de A 4 sur A 3 = Z 3 . On a la suite exacte V → A 4 → A 3 = Z 3 . Dans la théorie de Galois , cette application, ou plutôt la carte correspondante S 4 → S 3 , correspond à associer la cubique résolvante de Lagrange à une quartique, ce qui permet de résoudre le polynôme quartique par des radicaux, comme établi par Lodovico Ferrari .
Classes de conjugaison
Comme dans le groupe symétrique , deux éléments quelconques de A n conjugués par un élément de A n doivent avoir la même forme de cycle . Cependant, l'inverse n'est pas nécessairement vrai. Si la forme de cycle se compose uniquement de cycles de longueur impaire sans deux cycles de même longueur, où les cycles de longueur un sont inclus dans le type de cycle, alors il y a exactement deux classes de conjugaison pour cette forme de cycle ( Scott 1987 , §11.1, p299 ).
Exemples:
- Les deux permutations (123) et (132) ne sont pas conjuguées en A 3 , bien qu'elles aient la même forme de cycle, et donc conjuguées en S 3 .
- La permutation (123) (45678) n'est pas conjuguée à son inverse (132) (48765) en A 8 , bien que les deux permutations aient la même forme de cycle, elles sont donc conjuguées en S 8 .
Relation avec le groupe symétrique
- Voir Groupe symétrique .
Générateurs et relations
Un n est généré par 3 cycles, puisque 3 cycles peuvent être obtenus en combinant des paires de transpositions. Ce groupe électrogène est souvent utilisé pour prouver que A n est simple pour n ≥ 5 .
Groupe d'automorphisme
| n | Aut (A n ) | Sortie (A n ) |
|---|---|---|
| n ≥ 4, n ≠ 6 | S n | Z 2 |
| n = 1, 2 | Z 1 | Z 1 |
| n = 3 | Z 2 | Z 2 |
| n = 6 | S 6 ⋊ Z 2 | V = Z 2 × Z 2 |
Pour n > 3 , sauf pour n = 6 , le groupe d'automorphisme de A n est le groupe symétrique S n , avec le groupe d'automorphisme interne A n et le groupe d'automorphisme externe Z 2 ; l'automorphisme externe provient de la conjugaison par une permutation impaire.
Pour n = 1 et 2, le groupe d'automorphisme est trivial. Pour n = 3, le groupe d'automorphisme est Z 2 , avec un groupe d'automorphisme interne trivial et un groupe d'automorphisme externe Z 2 .
Le groupe d'automorphisme externe de A 6 est le groupe à quatre groupes de Klein V = Z 2 × Z 2 , et est lié à l'automorphisme externe de S 6 . L'automorphisme externe supplémentaire dans A 6 permute les 3 cycles (comme (123)) avec des éléments de forme 3 2 (comme (123) (456) ).
Isomorphismes exceptionnels
Il existe des isomorphismes exceptionnels entre certains des petits groupes alternés et des petits groupes de type Lie , en particulier les groupes linéaires spéciaux projectifs . Ceux-ci sont:
- A 4 est isomorphe à PSL 2 (3) et au groupe de symétrie de symétrie tétraédrique chirale .
- A 5 est isomorphe à PSL 2 (4), PSL 2 (5) et le groupe de symétrie de symétrie icosaédrique chirale . (Voir pour un isomorphisme indirect de PSL 2 (F 5 ) → A 5 en utilisant une classification de groupes simples d'ordre 60, et ici pour une preuve directe).
- A 6 est isomorphe à PSL 2 (9) et PSp 4 (2) '.
- A 8 est isomorphe à PSL 4 (2).
Plus évidemment, A 3 est isomorphe au groupe cyclique Z 3 , et A 0 , A 1 et A 2 sont isomorphes au groupe trivial (qui est aussi SL 1 ( q ) = PSL 1 ( q ) pour tout q ).
Exemples S 4 et A 4

Tableau de Cayley du groupe symétrique S 4
Les permutations impaires sont colorées: Transpositions en vert et 4 cycles en orange |

Tableau de Cayley du groupe alterné A 4
éléments: Les permutations paires (l'identité, huit 3-cycles et trois doubles transpositions (doubles transpositions en gras)) Sous-groupes:     
|
 A 3 = Z 3 (ordre 3) |
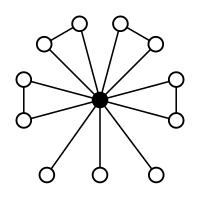 A 4 (ordre 12) |
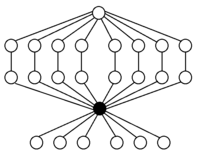 A 4 × Z 2 (commande 24) |
 S 3 = Dih 3 (ordre 6) |
 S 4 (ordre 24) |
 A 4 en S 4 à gauche |
Exemple A 5 en tant que sous-groupe de rotations à 3 espaces
A 5 est le groupe d'isométries d'un dodécaèdre dans l'espace 3, il y a donc une représentation A 5 → SO 3 ( R ) .
Dans cette image, les sommets des polyèdres représentent les éléments du groupe, le centre de la sphère représentant l'élément d'identité. Chaque sommet représente une rotation autour de l'axe pointant du centre vers ce sommet, d'un angle égal à la distance de l'origine, en radians. Les sommets d'un même polyèdre appartiennent à la même classe de conjugaison. Puisque l'équation de classe de conjugaison pour A 5 est 1 + 12 + 12 + 15 + 20 = 60 , nous obtenons quatre polyèdres distincts (non triviaux).
Les sommets de chaque polyèdre sont en correspondance bijective avec les éléments de sa classe de conjugaison, à l'exception de la classe de conjugaison de (2,2) -cycles, qui est représentée par un icosidodécaèdre sur la surface externe, avec ses sommets antipodaux identifiés par l'un l'autre. La raison de cette redondance est que les rotations correspondantes sont de π radians, et peuvent donc être représentées par un vecteur de longueur π dans l'une ou l'autre des deux directions. Ainsi, la classe des (2,2) cycles contient 15 éléments, tandis que l'icosidodécaèdre a 30 sommets.
Les deux classes de conjugaison de douze 5-cycles dans A 5 sont représentées par deux icosaèdres, de rayons 2 π / 5 et 4 π / 5, respectivement. L'automorphisme externe non trivial dans Out (A 5 ) ≃ Z 2 intervertit ces deux classes et les icosaèdres correspondants.
Exemple: le puzzle 15
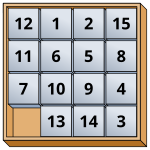
On peut prouver que le puzzle 15 , un exemple célèbre du puzzle coulissant , peut être représenté par le groupe alterné A 15 , car les combinaisons du puzzle 15 peuvent être générées par 3 cycles . En fait, tout puzzle glissant de 2 k - 1 avec des tuiles carrées de taille égale peut être représenté par A 2 k −1 .
Sous-groupes
A 4 est le plus petit groupe démontrant que l'inverse du théorème de Lagrange n'est pas vrai en général: étant donné un groupe fini G et un diviseur d de | G |, il n'existe pas forcément de sous-groupe de G d'ordre d : le groupe G = A 4 , d'ordre 12, n'a pas de sous-groupe d'ordre 6. Un sous-groupe de trois éléments (engendré par une rotation cyclique de trois objets) avec tout élément distinct non trivial génère le groupe entier.
Pour tout n > 4 , A n n'a pas de sous-groupes normaux non triviaux (c'est-à-dire corrects) . Ainsi, A n est un groupe simple pour tout n > 4 . A 5 est le plus petit groupe non résoluble .
Homologie de groupe
L' homologie de groupe des groupes alternés présente une stabilisation, comme dans la théorie de l'homotopie stable : pour n suffisamment grand , elle est constante. Cependant, il existe une homologie exceptionnelle de faible dimension. Notez que l' homologie du groupe symétrique présente une stabilisation similaire, mais sans les exceptions de faible dimension (éléments d'homologie supplémentaires).
H 1 : abélianisation
Le premier groupe d'homologie coïncide avec l' abélianisation , et (puisque A n est parfait , sauf pour les exceptions citées) est donc:
- H 1 (A n , Z) = Z 1 pour n = 0, 1, 2;
-
H 1 (A 3 , Z) = A à partir de
3 = A 3 = Z 3 ; -
H 1 (A 4 , Z) = A à partir de
4 = Z 3 ; - H 1 (A n , Z) = Z 1 pour n ≥ 5.
Ceci est facilement visible directement, comme suit. Un n est généré par 3 cycles - donc les seules cartes d'abélianisation non triviales sont A n → Z 3 , puisque les éléments d'ordre 3 doivent correspondre aux éléments d'ordre 3 - et pour n ≥ 5, tous les 3 cycles sont conjugués, donc ils doivent correspondre au même élément dans l'abélianisation, car la conjugaison est triviale dans les groupes abéliens. Ainsi, un 3-cycle comme (123) doit correspondre au même élément que son inverse (321), mais doit donc correspondre à l'identité, car il doit alors avoir un ordre divisant 2 et 3, de sorte que l'abélianisation est triviale.
Pour n <3 , A n est trivial, et a donc une abélianisation triviale. Pour A 3 et A 4, on peut calculer l'abélianisation directement, en notant que les 3-cycles forment deux classes de conjugaison (plutôt que toutes étant conjuguées) et qu'il existe des cartes non triviales A 3 ↠ Z 3 (en fait un isomorphisme) et A 4 ↠ Z 3 .
H 2 : multiplicateurs de Schur
Les multiplicateurs de Schur des groupes alternés A n (dans le cas où n vaut au moins 5) sont les groupes cycliques d'ordre 2, sauf dans le cas où n vaut soit 6 soit 7, auquel cas il y a aussi une triple couverture. Dans ces cas, alors, le multiplicateur de Schur est (le groupe cyclique) d'ordre 6. Ceux-ci ont été calculés pour la première fois dans ( Schur 1911 ).
- H 2 (A n , Z) = Z 1 pour n = 1, 2, 3;
- H 2 (A n , Z) = Z 2 pour n = 4, 5;
- H 2 (A n , Z) = Z 6 pour n = 6, 7;
- H 2 (A n , Z) = Z 2 pour n ≥ 8.
Remarques
Les références
- Robinson, Derek John Scott (1996), Un cours sur la théorie des groupes , Textes diplômés en mathématiques, 80 (2 éd.), Springer, ISBN 978-0-387-94461-6
- Schur, Issai (1911), "Über die Darstellung der symetrischen und der alternierenden Gruppe durch gebrochene lineare Substitutionen", Journal für die reine und angewandte Mathematik , 139 : 155-250, doi : 10.1515 / crll.1911.139.155
- Scott, WR (1987), Théorie des groupes , New York: Dover Publications , ISBN 978-0-486-65377-8


