Klein quatre-groupe - Klein four-group

Structure algébrique → Théorie des groupes Théorie des groupes
Notions de base Sous-groupe Sous-groupe normal Groupe de quotients Produit (semi-) direct Homomorphismes de groupe noyau image somme directe produit de couronne Facile fini infini continu multiplicatif additif cyclique abélien dièdre nilpotent soluble action Glossaire de la théorie des groupes Liste des sujets de théorie des groupes
Groupes finis Classification des groupes simples finis cyclique en alternance Type de mensonge sporadique Le théorème de Cauchy Le théorème de Lagrange Théorèmes de Sylow théorème de Hall groupe p Groupe abélien élémentaire Groupe Frobenius Multiplicateur de Schur Groupe symétrique S n Klein quatre groupe V Groupe dièdre D n Groupe de quaternions Q Groupe dicyclique Dic n
Groupes discrets Treillis Entiers ( )${\displaystyle \mathbb {Z} }$ Groupe gratuit Groupes modulaires PSL(2, )${\displaystyle \mathbb {Z} }$ SL(2, )${\displaystyle \mathbb {Z} }$ Groupe arithmétique Treillis Groupe hyperbolique
Groupes topologiques et de Lie Solénoïde Cercle GL linéaire général ( n ) Linéaire spécial SL( n ) O orthogonal ( n ) Euclidienne E( n ) Spécial orthogonal SO( n ) Unitaire U( n ) Unité spéciale SU( n ) Sp symplectique ( n ) G 2 F 4 E 6 E 7 E 8 Lorentz Poincaré Conforme Difféomorphisme Boucle Groupe de Lie de dimension infinie O(∞) SU(∞) Sp(∞)
Groupes algébriques Groupe algébrique linéaire Groupe réducteur Variété abélienne Courbe elliptique
v t e

En mathématiques , le groupe des quatre de Klein est un groupe à quatre éléments, dans lequel chaque élément est auto-inverse (le composer avec lui-même produit l'identité) et dans lequel la composition de deux des trois éléments non identitaires produit le troisième. Il peut être décrit comme le groupe de symétrie d'un rectangle non carré (avec les trois éléments non identitaires étant une réflexion horizontale et verticale et une rotation de 180 degrés), comme le groupe d' opérations exclusives ou binaires sur des valeurs binaires à deux bits, ou plus abstraitement comme Z ₂ × Z ₂ , le produit direct de deux copies du groupe cyclique d' ordre 2. Il a été nommé Vierergruppe (ce qui signifie quatre groupes) par Felix Klein en 1884. Il est aussi appelé le groupe de Klein , et est souvent symbolisé par la lettre V ou par K ₄ .

Le groupe des quatre de Klein, avec quatre éléments, est le plus petit groupe qui n'est pas un groupe cyclique . Il n'y a qu'un seul autre groupe d'ordre quatre, à isomorphisme près , le groupe cyclique d'ordre 4. Les deux sont des groupes abéliens . Le plus petit groupe non abélien est le groupe symétrique de degré 3 , qui est d'ordre 6.

Présentations

La table de Cayley du groupe Klein est donnée par :

Le groupe des quatre de Klein est également défini par la présentation du groupe

${\displaystyle \mathrm {V} =\left\langle a,b\mid a^{2}=b^{2}=(ab)^{2}=e\right\rangle .}$

Tous les éléments non identitaires du groupe de Klein sont d'ordre 2, ainsi deux éléments non identitaires peuvent servir de générateurs dans la présentation ci-dessus. Le groupe des quatre de Klein est le plus petit groupe non cyclique . C'est cependant un groupe abélien , et isomorphe au groupe dièdre d'ordre (cardinalité) 4, c'est-à-dire D ₄ (ou D ₂ , selon la convention géométrique) ; à part le groupe d'ordre 2, c'est le seul groupe dièdre qui soit abélien.

Le quatre-groupe de Klein est également isomorphe à la somme directe Z ₂ Z ₂ , de sorte qu'il peut être représenté par les paires {(0,0), (0,1), (1,0), (1,1 )} sous l'addition au niveau des composants modulo 2 (ou de manière équivalente les chaînes de bits {00, 01, 10, 11} sous XOR au niveau du bit ); avec (0,0) étant l'élément d'identité du groupe. Le quatre-groupe de Klein est donc un exemple d'un 2-groupe abélien élémentaire , qui est aussi appelé un groupe booléen . Le quatre-groupe de Klein est donc aussi le groupe engendré par la différence symétrique comme l'opération binaire sur les sous - ensembles d'un ensemble de puissances d'un ensemble à deux éléments, c'est-à-dire sur un corps d'ensembles à quatre éléments, par exemple ; l' ensemble vide est l'élément d'identité du groupe dans ce cas. ${\displaystyle \{\emptyset ,\{\alpha \},\{\beta \},\{\alpha ,\beta \}\}}$

Une autre construction numérique du groupe des quatre de Klein est l'ensemble { 1, 3, 5, 7 }, l'opération étant la multiplication modulo 8 . Ici a vaut 3, b vaut 5 et c = ab vaut 3 × 5 = 15 7 (mod 8) .

Le groupe des quatre de Klein a une représentation sous forme de matrices réelles 2 × 2, l'opération étant la multiplication matricielle :

${\displaystyle e={\begin{pmatrix}1&0\\0&1\end{pmatrix}},\quad a={\begin{pmatrix}1&0\\0&-1\end{pmatrix}},\quad b={ \begin{pmatrix}-1&0\\0&1\end{pmatrix}},\quad c={\begin{pmatrix}-1&0\\0&-1\end{pmatrix}}}$

Géométrie

Le groupe de symétrie de cette croix est le groupe des quatre de Klein. Il peut être retourné horizontalement ( a ) ou verticalement ( b ) ou les deux ( ab ) et rester inchangé. Contrairement à un carré, cependant, une rotation d'un quart de tour changera la figure.

Géométriquement, en deux dimensions le groupe des quatre de Klein est le groupe de symétrie d'un losange et de rectangles qui ne sont pas des carrés , les quatre éléments étant l'identité, la réflexion verticale, la réflexion horizontale et une rotation à 180 degrés.

En trois dimensions, il existe trois groupes de symétrie différents qui sont algébriquement le groupe de Klein V :

• un avec trois axes de rotation perpendiculaires d'ordre 2 : D ₂
• un avec un axe de rotation d'ordre 2 et un plan de réflexion perpendiculaire : C _{2 h} = D _{1 d}
• un avec un axe de rotation d'ordre 2 dans un plan de réflexion (et donc aussi dans un plan de réflexion perpendiculaire) : C _{2 v} = D _{1 h} .

Représentation de permutation

Identité et double- transpositions de quatre objets forme V

Autres permutations de quatre objets, formant V également.

Voir 4 sous-ensembles d'éléments de S ₄

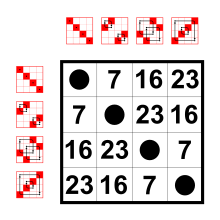
Les trois éléments d'ordre deux du groupe des quatre de Klein sont interchangeables : le groupe d'automorphisme de V est le groupe des permutations de ces trois éléments.

Les permutations du groupe des quatre de Klein de ses propres éléments peuvent être considérées de manière abstraite comme sa représentation de permutation sur quatre points :

V = { (), (1,2)(3,4), (1,3)(2,4), (1,4)(2,3) }

Dans cette représentation, V est un sous - groupe du groupe alterné A ₄ (et aussi le groupe symétrique S ₄ ) sur quatre lettres. En fait, c'est le noyau d'un homomorphisme de groupe surjectif de S ₄ à S ₃ .

Les autres représentations au sein de S ₄ sont :

{ (), (1,2), (3,4), (1,2)(3,4)}

{ (), (1,3), (2,4), (1,3)(2,4)}

{ (), (1,4), (2,3), (1,4)(2,3)}

Ce ne sont pas des sous-groupes normaux de S _4.

Algèbre

D'après la théorie de Galois , l'existence du groupe des quatre de Klein (et en particulier sa représentation par permutation) explique l'existence de la formule de calcul des racines des équations quartiques en termes de radicaux , telle qu'établie par Lodovico Ferrari : la carte S ₄ → S ₃ correspond à la cubique résolvante, en termes de résolvantes de Lagrange .

Dans la construction d' anneaux finis , huit des onze anneaux à quatre éléments ont le groupe de Klein comme sous-structure additive.

Si R ^× désigne le groupe multiplicatif de réels non nuls et R ⁺ le groupe multiplicatif de réels positifs , R ^× × R ^× est le groupe d'unités de l'anneau R × R , et R ⁺ × R ⁺ est un sous-groupe de R ^× × R ^× (en fait c'est la composante de l'identité de R ^× × R ^× ). Le groupe quotient ( R ^× × R ^× ) / ( R ⁺ × R ⁺ ) est isomorphe au quatre-groupe de Klein. De la même manière, le groupe d'unités de l' anneau des nombres complexes divisés, lorsqu'il est divisé par sa composante d'identité, donne également le groupe à quatre de Klein.

La théorie des graphes

Le graphe connexe simple le plus simple qui admet le groupe des quatre de Klein comme groupe d' automorphisme est le graphe en losange illustré ci-dessous. C'est aussi le groupe d'automorphismes de certains autres graphes qui sont plus simples dans le sens où ils ont moins d'entités. Il s'agit notamment du graphe à quatre sommets et d'une arête, qui reste simple mais perd sa connectivité, et le graphe à deux sommets connectés entre eux par deux arêtes, qui reste connecté mais perd de sa simplicité.

La musique

En composition musicale, le groupe à quatre est le groupe de base des permutations de la technique des douze tons . Dans ce cas, la table de Cayley est écrite ;

Voir également

• Groupe quaternion
• Liste des petits groupes

Les références

Lectures complémentaires

• MA Armstrong (1988) Groupes et symétrie , Springer Verlag , page 53 .
• WE Barnes (1963) Introduction à l'algèbre abstraite , DC Heath & Co., page 20.

Liens externes

• Weisstein, Eric W. "Vierergruppe" . MathWorld .